5.汉诺塔问题

OpenJudge - 6261:汉诺塔问题

---

解题思路：

（1）要将最左边柱子上的圆盘全部移动到中间柱，并且只能每次移动一个圆盘，小的只能放在大的上面，当圆盘只有两个的时候，只需要3步即可完成，如图所示： 

                     

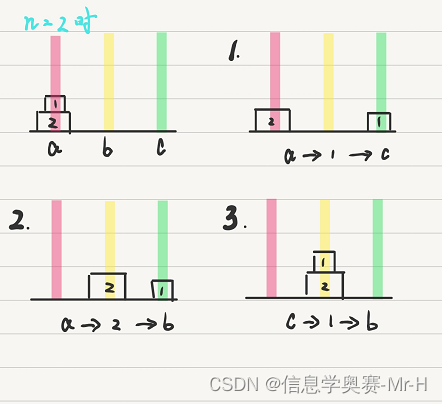
（2）当n=3，即要把左边的三个圆盘放入中间柱的话，需要7步完成，如下图所示： 

                    

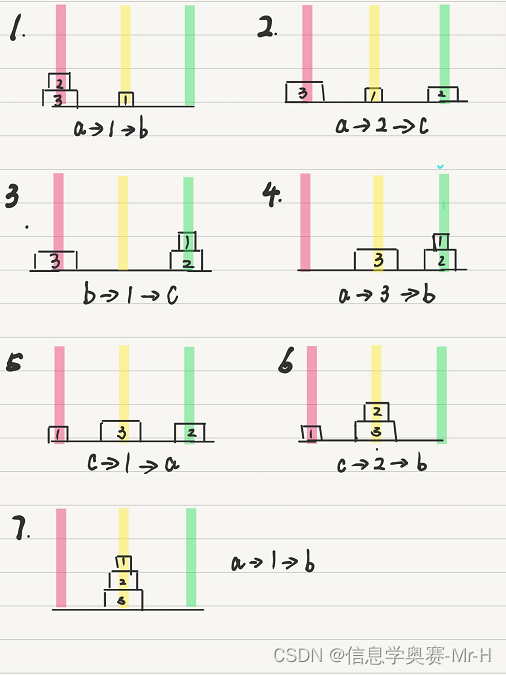
 （3）当我们把最大的圆盘看为一部分，他上面的看成一个整体的时候，那么3步即可完成，如下图所示：

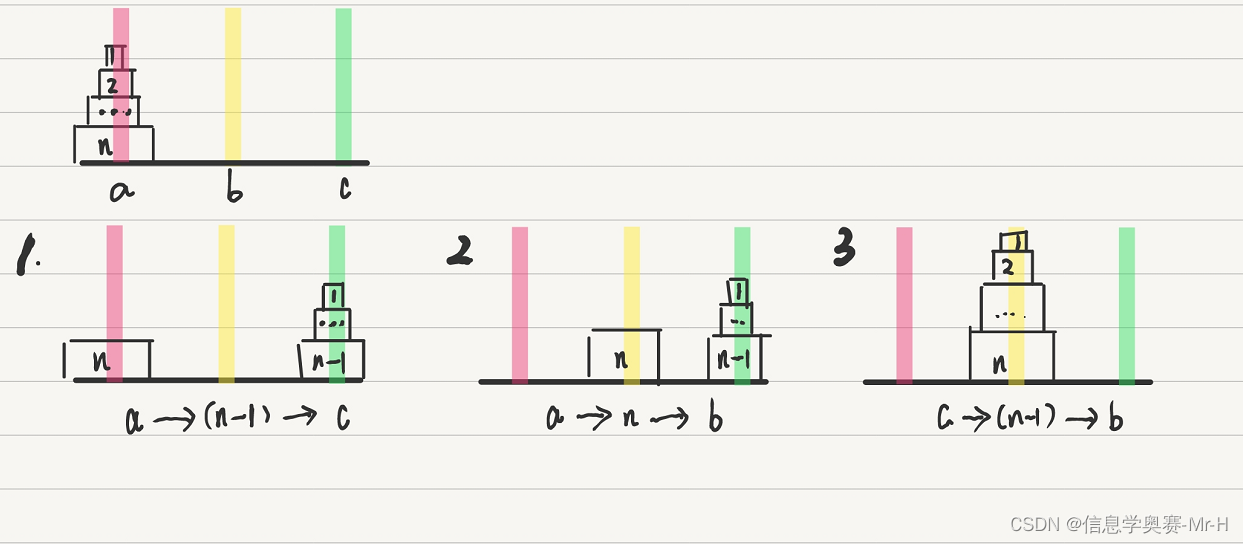
（4） 上述图示基本明白了，如果要解决将n个圆盘从a移动到b的话，可以分解为规模更小的子问题，如果利用递归思想解题的话，最小的子问题也就是出口到底在哪里呢？最小的子问题也就是1个圆盘的时候，直接从a柱移动到b柱即可。

（5）那么当圆盘有两个的时候，因为大盘上面只能落小盘，1号圆盘必须经过b柱先去c柱，这样，2号盘才能一下移动到b柱，然后再将1号盘从c柱移动到b柱

（6）着重分析三个盘子的时候，首先把1号和2号绑在一起，他俩需要跨过b柱放到c柱

         步骤1为move（2,a,c,b）即a柱是初始地点，c是目标地点，b是过渡地点

         步骤2为将3号盘从a柱移动到b柱，cout<<a<<3<<b;（因为只有一个盘子，直接操作）

         步骤3为将1号和2号盘从c柱移动到b柱，因为不能一次性移动，所以要借助a柱，即move（2，c,b,a）

（7）在上述步骤1的时候，将1和2号盘移动到c柱的时候，又发生了3个步骤

          步骤1.1 将1号圆盘放到b柱

          步骤1.2 将2号圆盘放到c柱

          步骤1.3 将1号圆盘放到c柱

（8）在上述步骤3的时候，将1和2号盘移动到b柱的时候，同样发生了3个步骤

          步骤3.1 将1号圆盘放到a柱

          步骤3.2 将2号圆盘放到b柱

          步骤3.3 将1号圆盘放到b柱

（9）在解决递归问题的时候，分析出可以利用递归思想即可，要去找递归出口和子问题的表达式，如何找到表达式，就找最小子问题和次二小子问题的关系，不要去想过于冗杂的数据和过程，

       设move（n,a,b,c）函数为将n个圆盘从a柱（初始柱）移到b柱（目标柱），c柱（过渡柱），那么递归的出口应该是，if（n==1）cout<<a<<"->"<<n<<"->"<<b<<endl;

      将n-1个盘子从a柱转移到c柱，b为过渡柱，即move（n-1,a,c,b）；

      然后将第n个盘子从a柱直接转移到b柱，cout<<a<<"->"<<n<<"->"<<b<<endl;

      最后将n-1个盘子从c柱转移到b柱，a为过渡柱，即move（n-1，c,b,a）；

---

#include<bits/stdc++.h>
using namespace std;
void move(int n,char a,char b,char c)
{
	if(n==1)//递归出口 
	cout<<a<<"->"<<n<<"->"<<b<<endl;//只有一个盘子，直接从a放到b 
	else
	{
		move(n-1,a,c,b);//将n-1个盘子从a柱放到c柱，b为过渡柱 
		cout<<a<<"->"<<n<<"->"<<b<<endl;//将第n个盘子从a柱移到b柱 
		move(n-1,c,b,a);//将n-1个盘子从c柱移到b柱，a为过渡柱 
	}
} 
int main()
{
	int m;
	char x,y,z;
	cin>>m;
	cin>>x>>y>>z;
	move(m,x,y,z);
	return 0;
}