2001年-数的计算

原创已于 2022-09-29 11:14:49 修改 · 314 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #蓝桥杯 #算法

于 2022-09-29 11:14:28 首次发布

信息学奥赛普及组第一题专栏收录该内容

24 篇文章

订阅专栏

这篇文章介绍了如何使用递归和动态规划的方法解决数的拆分问题，通过计算每个数字可以由比它小一半的数组合而成的方案数，展示了从大问题分解到小问题的解决策略。关键步骤包括初始化、递推公式和长整型数组的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

[NOIP2001 普及组] 数的计算 - 洛谷

解题思路：

（1）每一个数的左边都只能加上比它二分之一小的数，每一个数的的大问题都可以从比它小规模的子问题来拼凑而成，如下图所示：

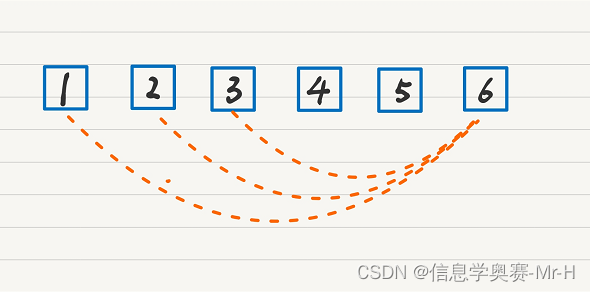
（2）如果要求数字6的方案数，那么必须要知道1,2,3的方案数，这样的话形成了解决大问题必须先解决小问题的思路，符合递推（动态规划）的思想

（3）设f【n】是数字n的方案数，因为本身的数字也算一个数，所以f【n】都初始化为1

（4）递推公式为f【i】=f【i】+f【j】，循环枚举1-j（i/2）的方案数，依次累加即可。

（5）数字1000的方案数可能很大，所以使用long long 数组

#include<bits/stdc++.h>
using namespace std;

long long f[1010];

int main()
{
	int n;
	cin>>n;
	
	for(int i=1;i<=1000;i++)
	f[i]=1;
	
	for(int i=2;i<=n;i++)
	{
		for(int j=1;j<=i/2;j++)
		{
			f[i]=f[i]+f[j];
		}
	}

	cout<<f[n];
	return 0;
}