【Transformer】位置embedding的理解

最新推荐文章于 2025-03-19 02:45:00 发布

百万年薪天才少女

最新推荐文章于 2025-03-19 02:45:00 发布

阅读量831

点赞数 29

分类专栏：人工智能文章标签： transformer embedding 深度学习

本文链接：https://blog.youkuaiyun.com/weixin_54607024/article/details/144797507

版权

人工智能专栏收录该内容

14 篇文章

订阅专栏

Transformer 中除了单词的 Embedding，还需要使用位置 Embedding 表示单词出现在句子中的位置。因为 Transformer 不采用 RNN 的结构（RNN 是一种顺序模型，它通过一个个单词的顺序来处理信息，能够捕捉到单词之间的时间依赖关系），然而，Transformer 采用的是自注意力机制（self-attention），它可以在处理输入时同时考虑整个序列中的所有单词。这种机制使得模型能够捕捉到全局信息，但也导致了一个问题：单词的顺序信息在处理时没有利用。而这部分信息对于自然语言处理来说非常重要。所以 Transformer 中使用位置 Embedding 保存单词在序列中的相对或绝对位置。

位置 Embedding 用 PE表示，PE 的维度与单词 Embedding 是一样的。PE 可以通过训练得到，也可以使用某种公式计算得到。

直观思考，要想给输入的向量添加位置信息, 最先想到的无疑就是直接使用1 , 2 , 3 , . . . , n 这样的连续数字给输入向量赋予标号来表达向量的顺序。但是这样会导致一些问题:

如果模型没有见过比训练时更大的整数标记（如 101、102 等），它很难推断这些数字与已知位置标记（如 1 到 100 ）之间的关系，导致外推能力不足
当序列长度不断增大, 其位置标记也会越来越大, 不利于训练

所以进一步, 可以想将上面的位置标记进行归一化, 其中0表示第一个单词，1表示最后一个单词。这样就可以解决上面两个问题, 但是这样又会导致一些问题:

模型难以捕捉相对位置关系: 例如，标记值 0.5在长度为 3 的序列中表示第 2 个位置，但在长度为 7 的序列中表示第 4 个位置。
如果序列长度较长，[ 0 , 1 ] 范围内的连续分布可能导致相邻位置之间的差异非常小。

故而, 我们需要这样一种编码:

每个位置的编码值应该唯一
输入向量长度不同时, 其中每个分量间的相对距离保持一致
编码范围有界, 不会随输入向量长度增大而无限增大

在 Transformer 中采用了不同频率的正弦和余弦函数：

其中，pos 表示单词在句子中的位置，i是维度。d 表示 PE的维度 (与词 Embedding 一样)，2i 表示偶数的维度，2i+1 表示奇数维度 (即 2i≤d, 2i+1≤d)。我们选择这个函数是因为我们假设它允许模型轻松学习关注相对位置，因为对于任何固定的偏移量 k，PEpos+k 可以表示为 PEpos 的线性函数。

用 t 表示输入句子中需要的位置， $\vec{p_t}\in \mathbb{R}^d$ 表示对应的编码，其中 d 表示编码维度（d为偶数）。然后 f : N → $\mathbb{R}^d$ 表示产生输出向量 $\vec{p_t}$ 的函数，它被定义为

也就是说，位置编码的每个维度对应于一个正弦曲线。波长从 2π 到 10000 ·2π （频率 f从 1/10000到 1，λ = 2π/ f ），可以把位置嵌入 $\vec{p_t}$ 想象成一个包含每个频率的正余弦对的向量（注意 d 能被2整除）：

你可能会想这个正余弦的组合怎么能表示一个位置或者顺序呢？它实际上非常简单，假设你想要用一个二进制的形式表示一个数字，那会怎么样？

你可以观察到不同位之间变化的速度，最低位（红色数字）每个数字之间交替变化，第二低位（蓝）每两个数字翻转一次，以此类推。

但是用二进制值会在浮点世界里造成空间浪费。所以反过来，我们可以使用它们对应的浮点连续值——三角函数。实际上，它们等价于交替变换的位。而且，通过降低它们的频率，我们也可以实现从红色的位走到橙色的位。怎么理解呢？

对于上面的公式, 我们可以先单独看 $sin(w_it)$ ：

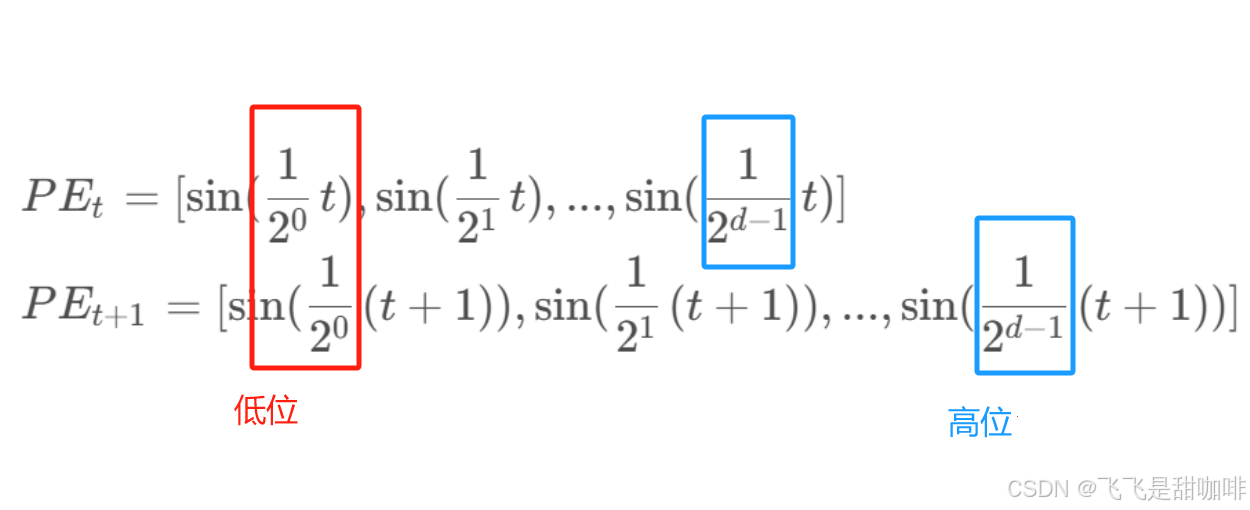
对于上式对于每一行, 随着维度从小到大, 使得 $sin(w_it)$ 的波长不断变大,此时 sin 函数对 t 的变动越不敏感, 对应二进制从低位到高位。

每一行都在上一行的基础上进行调整(t 的作用), 相当于二进制数从小到大。
低维度, 频率高, 随着t变换, 相当于二进制中的低位0/1不断频繁变换. 抽象来看, 能够捕捉局部信息。
高维度, 频率低, 随着t变换, 相当于二进制中的高位0/1不再像低位一样变换频繁，能够捕捉全局信息。

由于sin是周期函数，因此从纵向来看，如果函数的频率偏大，引起波长偏短，则不同 t 下的位置向量可能出现重合的情况。因此在transformer的论文中, 将频率设置为一个非常小的值来确保不同t 下的位置向量不会出现重合：

sin函数解决了:

每个位置的编码值应该唯一(t 不同, 位置编码不同)
输入向量的长度不同时, 其分量的相对位置一致(维度i 来确定)
编码范围有界，不会随输入向量长度增大而无限增大(sin ⁡函数取值为[0,1])

进一步, 我们想要要求: 不同的位置向量是可以通过线性转换得到的, 即:

T表示一个线性变换矩阵。观察这个式子，联想到在向量空间中一种常用的线形变换——旋转。在这里，我们将t想象为一个角度，那么Δ t 就是其旋转的角度，则上面的式子可以进一步写成：

然后我们就可以改写全是sin函数的位置编码公式, 使得位置编码的维度两两一组, 用sin 与cos 表示:

所以也就可以得到:

最终, 我们得到了transformer中的位置编码公式:

文章还尝试了使用训练到的位置嵌入，发现两种方法结果几乎相同。我们选择正弦函数方法，因为它可能允许模型推断出比训练期间遇到的序列长度更长的序列长度。

使用这种公式计算 PE 有以下的好处：

使 PE 能够适应比训练集里面所有句子更长的句子，假设训练集里面最长的句子是有 20 个单词，突然来了一个长度为 21 的句子，则使用公式计算的方法可以计算出第 21 位的 Embedding。
可以让模型容易地计算出相对位置，对于固定长度的间距 k，PE(pos+k) 可以用 PE(pos) 计算得到。因为 Sin(A+B) = Sin(A)Cos(B) + Cos(A)Sin(B), Cos(A+B) = Cos(A)Cos(B) - Sin(A)Sin(B)。

将单词的词 Embedding 和位置 Embedding 相加，就可以得到单词的表示向量 x，x 就是 Transformer 的输入。那为什么位置编码是和词嵌入向量是相加而不是将二者拼接起来？