对数正态分布(Log-Normal Distribution)是一种概率分布,其来源与数据的乘法性质密切相关。它起源于许多实际现象,主要与自然现象和经济活动相关。本质上,如果一个变量的对数服从正态分布,那么这个变量就是对数正态分布:
1. 定义与特性
- 对数正态分布的随机变量XX的对数(自然对数)Y=ln(X)服从正态分布,即:
Y∼N(μ,σ2)
- 其概率密度函数(PDF)表达为:
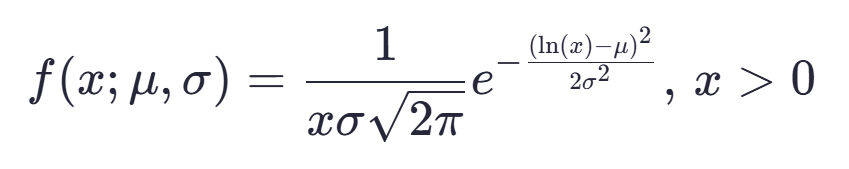
2. 推导
我们开始定义对数正态分布。给定一个随机变量 XX,如果它的对数 Y=ln(X)Y=ln(X) 服从正态分布,即:
Y∼N(μ,σ2)
正态分布的概率密度函数为:
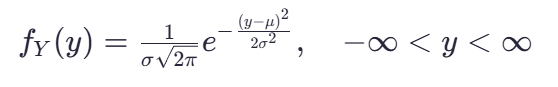
我们通过对数变换得到 XX 的概率密度函数。由于 Y=ln(X),我们需要找到 X的概率密度函数 ![]() 。
。
首先,设 ![]() 则 y=ln(x)。然后,我们需要对 x进行求导,得到
则 y=ln(x)。然后,我们需要对 x进行求导,得到 ![]()
根据概率密度函数变换的公式,若 Y 是 X 的函数,则 X 的概率密度函数可以表示为:
![]()
将 y换成 ln(x)并结合上述的 dy/dx 的表达式:
![]()
将![]() 替换为 ln(x)的值:
替换为 ln(x)的值:
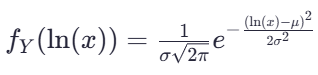
现在将![]() 的表达式代入
的表达式代入![]() 的公式:
的公式:
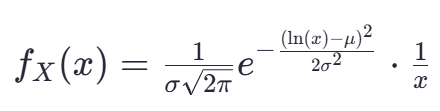
最终得到 X的概率密度函数,即对数正态分布的形式:
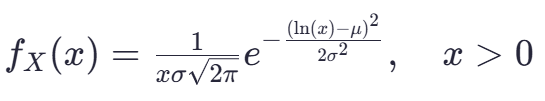
 正态分布与对数正态分布的关系
正态分布与对数正态分布的关系





















 2850
2850

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








