李哥AI第四章卷积神经网络&&CAU人工智能class3-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_53515170/article/details/146222456

分类任务：

回归任务和分类任务的区别：

为什么分类任务不用一个输出值：

因为在一个连续的数轴上，利用预测值和类别值更近的方法各个类别与预测点的距离各不相同，即各个类别不等价。在分类任务中只有是和不是的区别，没有哪一个更像的区别。

如何分类输出

有几个类就要有几个输出

图像识别初步：手写数字识别

该部分代码通过A飞浆ai studio实现，完整代码将置于文末

使用的库为paddle

MNIST数据集

该数据集由飞浆自带提供，可以直接使用

数据处理

#导入数据集Compose的作用是将用于数据集预处理的接口以列表的方式进行组合。
#导入数据集Normalize的作用是图像归一化处理，支持两种方式： 1. 用统一的均值和标准差值对图像的每个通道进行归一化处理； 2. 对每个通道指定不同的均值和标准差值进行归一化处理。
from paddle.vision.transforms import Compose, Normalize
transform = Compose([Normalize(mean=[127.5],std=[127.5],data_format='CHW')])
# 使用transform对数据集做归一化
print('下载并加载训练数据')
train_dataset = paddle.vision.datasets.MNIST(mode='train', transform=transform)
test_dataset = paddle.vision.datasets.MNIST(mode='test', transform=transform)
print('加载完成')

首先设定数据处理函数（该代码主要是做归一化操作）transform

最外层的Compose 的作用是将用于数据集预处理的接口以列表的方式进行组合。实际上就是将一系列图片处理的方法按顺序组合执行。

比如：

transform = Compose([
            Resize((256, 256)), # 改变尺寸大小
            CenterCrop((224, 224)), # 对输入图像进行裁剪，保持图片中心点不变
            RandomHorizontalFlip(0.5), # 随机水平翻转
            RandomRotation(degrees=15), # 旋转
            Normalize(mean=[127.5],std=[127.5],data_format='CHW') # 图像归一化
        ])

Normalize：图像归一化处理，支持两种方式：（1）用统一的均值和标准差值对图像的每个通道进行归一化处理；（2）对每个通道指定不同的均值和标准差值进行归一化处理

这里取127.5是因为是255 / 2 = 127.5

定义多层感知机

模型结构：

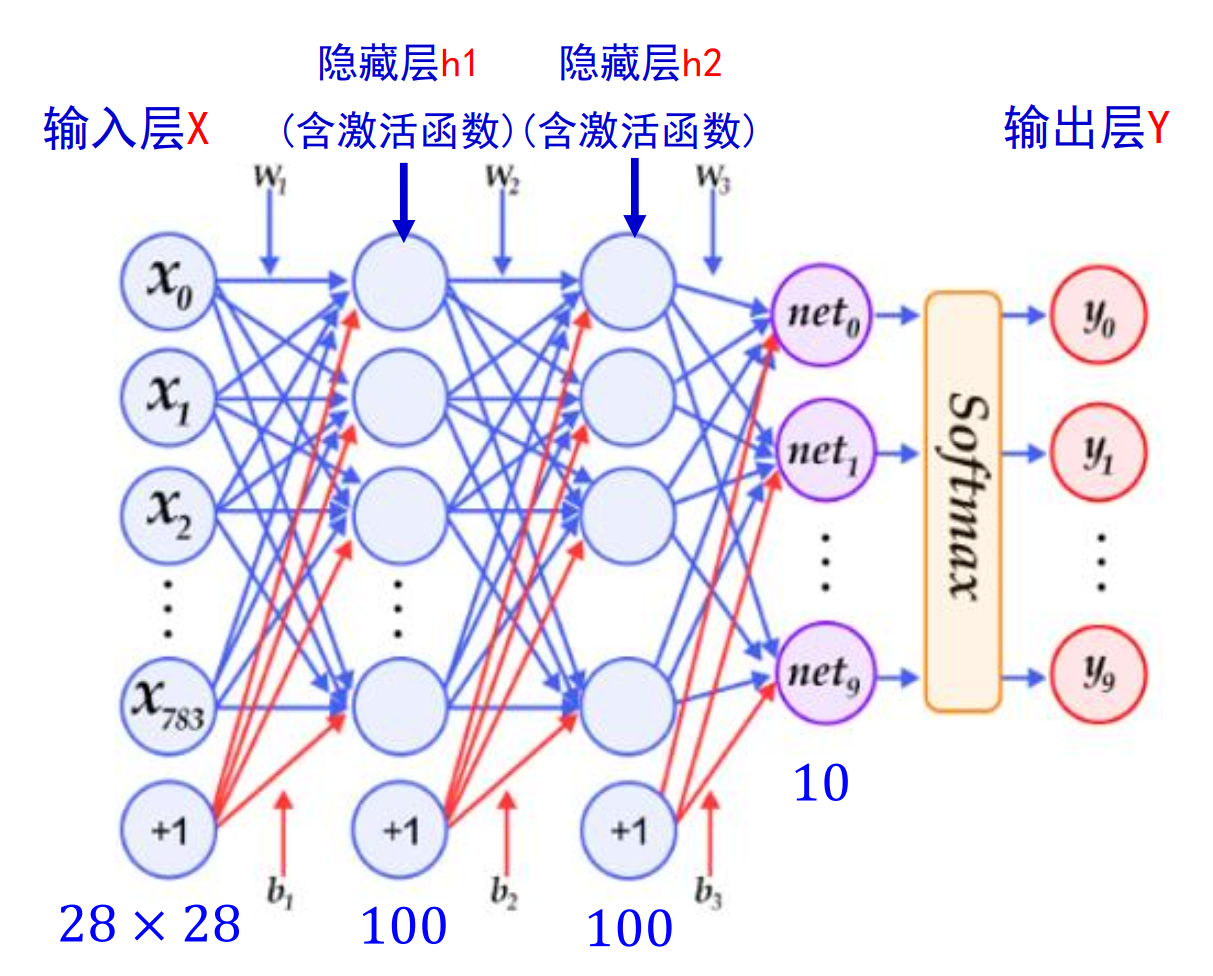
# 定义多层感知器 
#动态图定义多层感知器
class mnist(paddle.nn.Layer):
    def __init__(self):
        super(mnist,self).__init__()
        self.fc1 = nn.Linear(in_features =28*28, out_features =100)
        self.fc2 = nn.Linear(in_features =100, out_features =100)
        self.fc3 = nn.Linear(in_features =100, out_features =10)

    def forward(self, input_):
        x = paddle.reshape(input_, [input_.shape[0], -1])
        x = self.fc1(x)
        x = F.relu(x)
        x = self.fc2(x)
        x = F.relu(x)
        x = self.fc3(x)
        y = F.softmax(x)
        return y

激活函数用relu，层与层之间运用线性结构

最后的分类头使用了softmax

softmax

Softmax 函数也称为归一化指数函数，是逻辑函数的一种推广。它能将一个含任意实数的 K 维向量 z“压缩”到另一个 K 维实向量σ(z)中，使得每一个元素的范围都在 (0, 1)之间，并且所有元素的和为 1 。该函数多用于多分类问题中。

函数的分类原理：

封装模型和定义损失函数

from paddle.metric import Accuracy

# 用Model封装模型
model = paddle.Model(mnist())   

# 定义损失函数
optim = paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters())

# 配置模型
model.prepare(optim,paddle.nn.CrossEntropyLoss(),Accuracy())

首先要将写好的类封装成模型方便后续使用

损失函数

例子：

另外优化器这里用来Adam，不是SGD

最后配置模型。

模型训练并评估

# 训练保存并验证模型
model.fit(train_dataset,test_dataset,epochs=2,batch_size=64,save_dir='multilayer_perceptron',verbose=1)

最后是模型预测，这里不做展示

卷积神经网络

卷积的引入

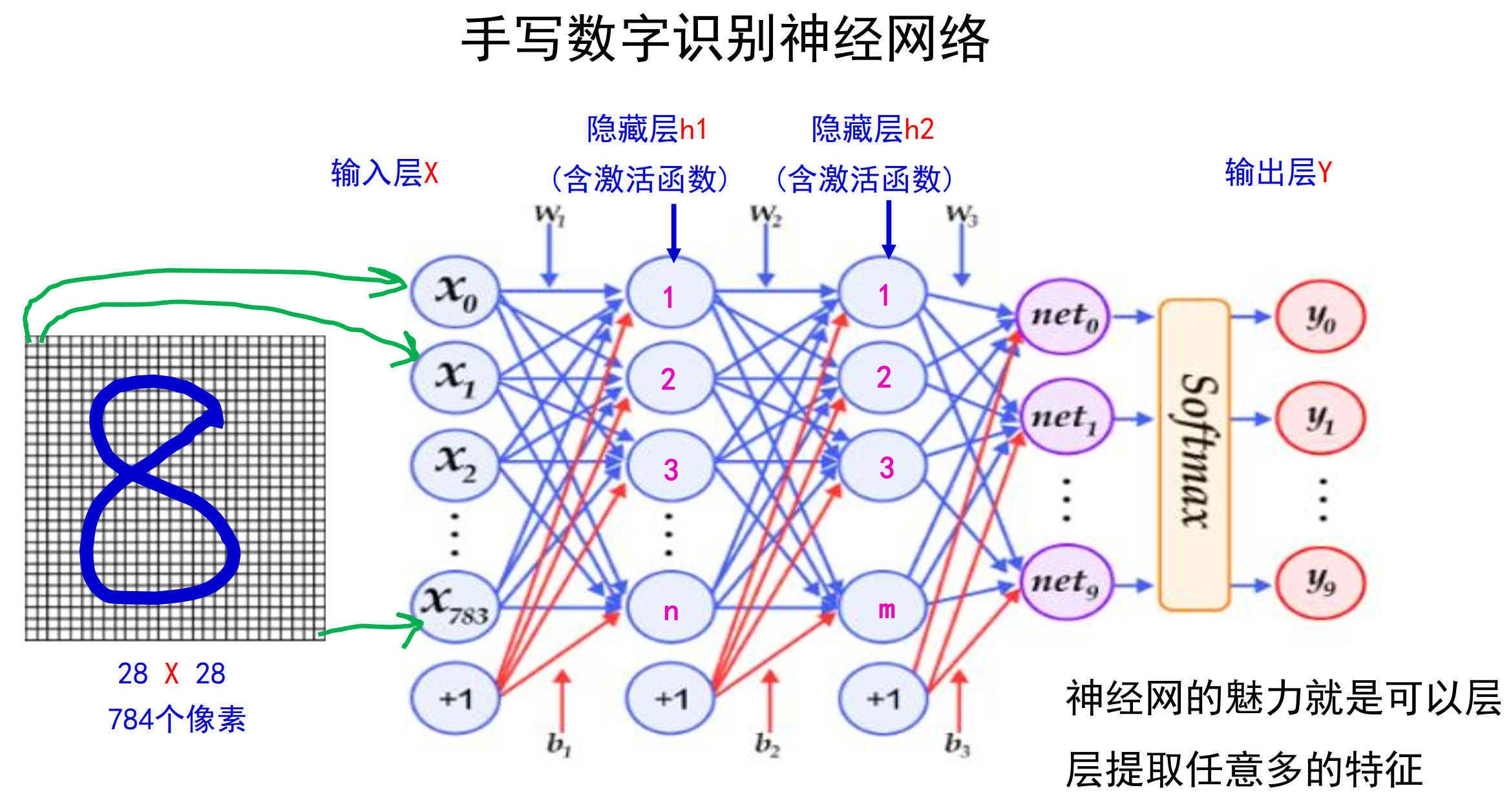
手写数字识别网络的不足：

只考虑了孤立的点没有考虑一个区域

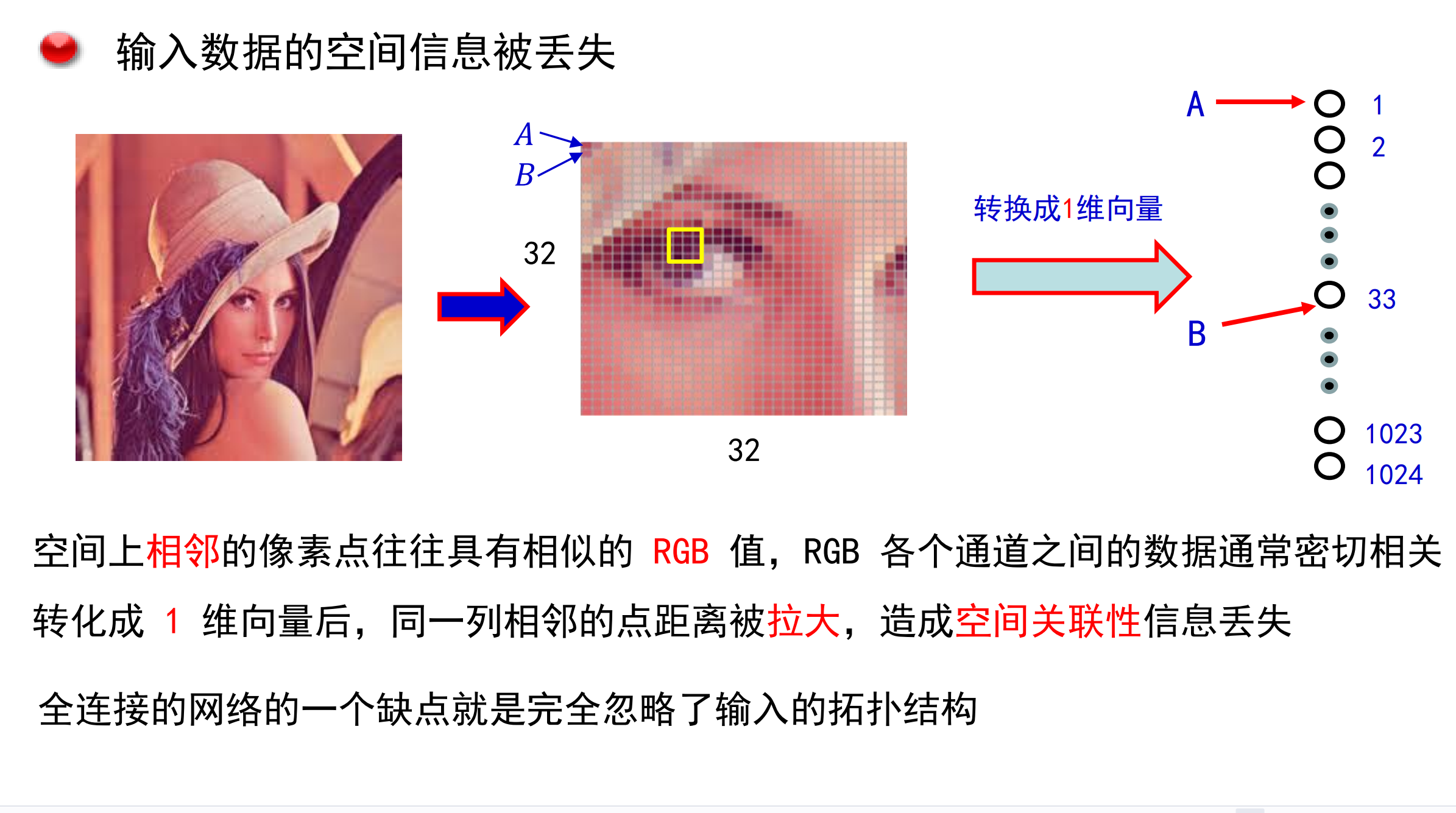
参数太多：

图像模型的三个特征发现

平移不变性

空间相关性

放缩

卷积神经网络由此提出。

卷积神经网络的原理

图片是矩阵：

直接将图片转化为矩阵展开数据过大，非常容易过拟合。

卷积神经网络的过程图：

卷积核

什么是卷积核

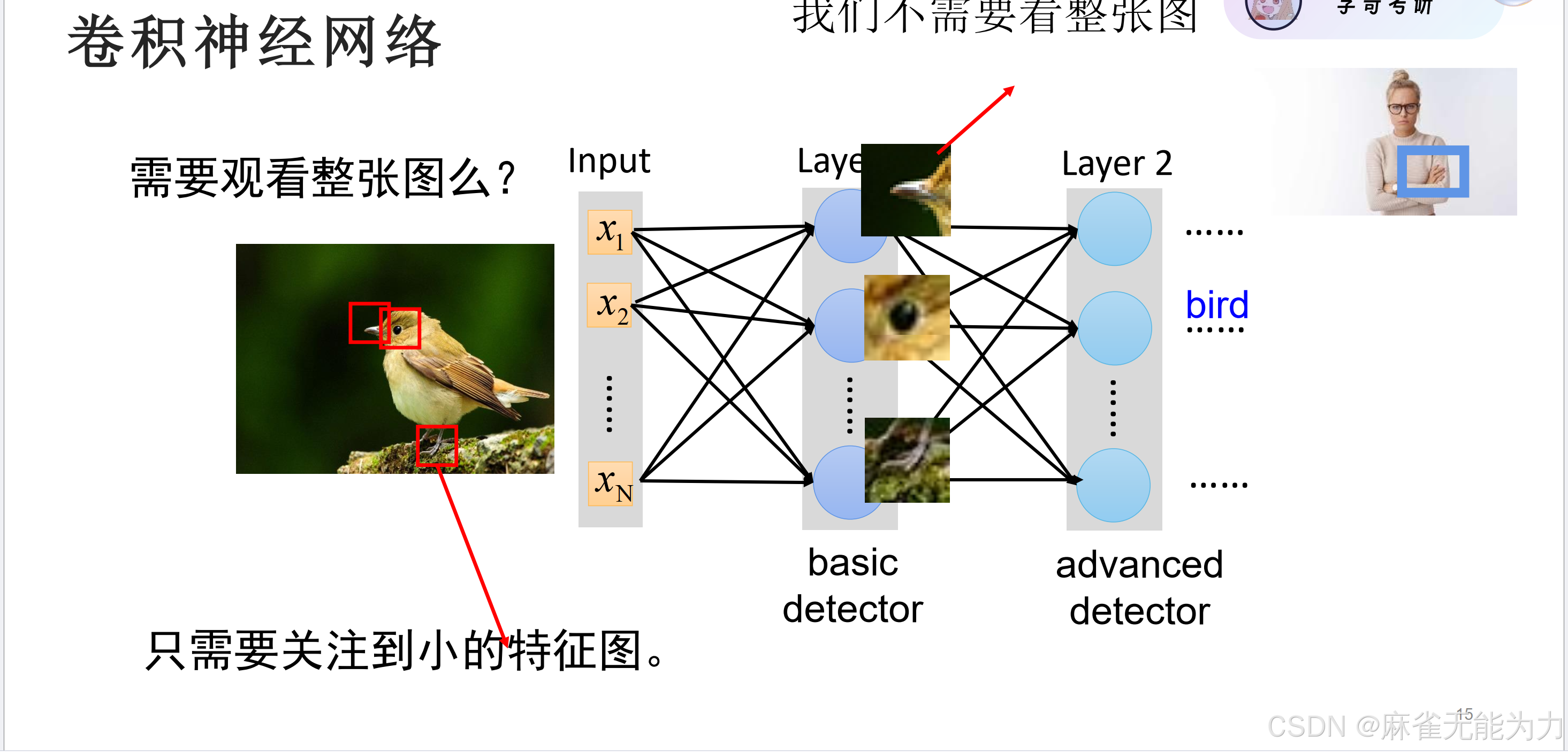
比如在这张鸟的图片中，鸟嘴，鸟眼就可以当成一个卷积核。

注意，这里只考虑了输入的通道为1的情况，所以卷积核是一个矩阵，而输入的通道往往很多，因此卷积核应是一组矩阵。

感受野

每一个特征图上像素对于原图的感知范围就是感受野

其中s依然代表步长，下图是一个感受野计算的例子

总之：卷积计算等于特征抽取

卷积神经网络的结构

填充

使用padding保持卷积后特征图大小不变：

填充的种类：

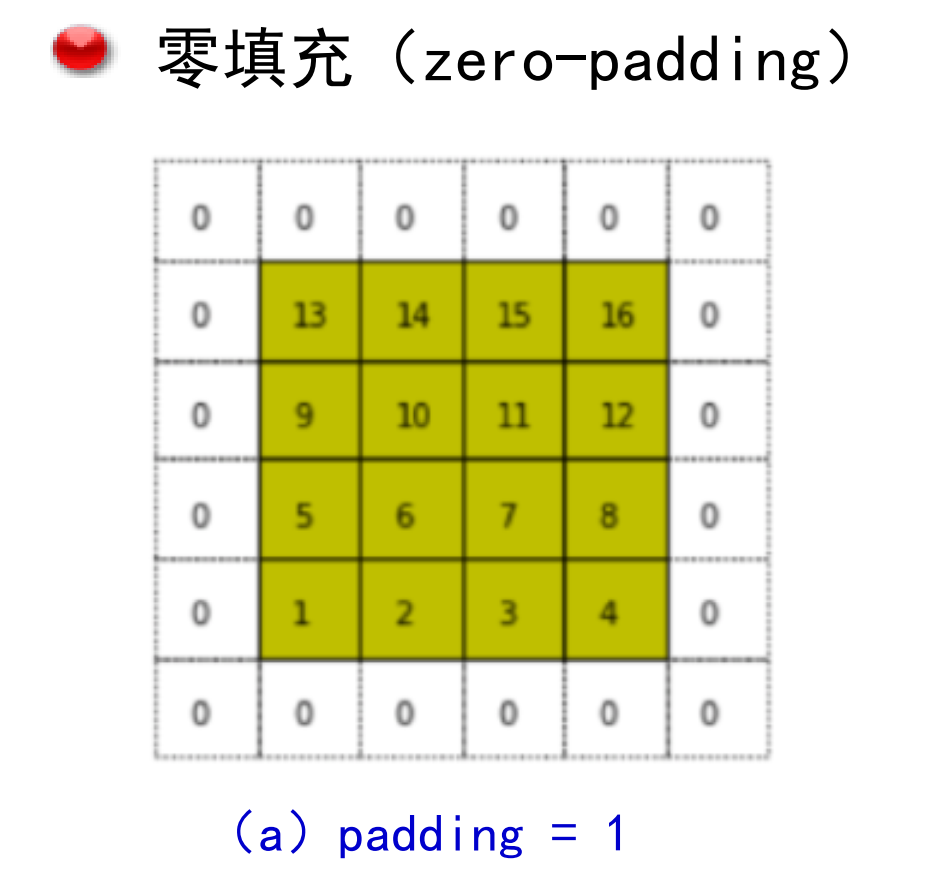
可以增加卷积和的大小和卷积核数量，增减训练的参数：

1.特征图长宽计算公式：

$I - k + 1 = O$

I：输入特征图长度

k：卷积核长度

O：输出特征图长度：

padding直接加在输入特征图上

2.由上面的公式得出一下结论

$P * 2 + 1 = k$

若该公式成立，则 I = O即输入特征图与输出特征图大小不变

3.一层卷积核参数的计算公式：

卷积核数量*卷积核层数*卷积核高度*卷积核宽度

以下是练习题：

降低特征图尺寸的方法：

特征图尺寸过大会使参数过多，有以下两种方式降低特征图的尺寸

方法一：

步长

降低采样，设置步长：

计算公式：

两个S均为步长

该方法会丢失数据，引入计算；

方法二：

池化

池化是对特征图缩小的一种操作，用各种方法分区域缩小特征图都能称为池化

池化的原理：

特征图中的相邻区域倾向于具有相似的值，因此通常卷积后输出值也具有相似的值。

这说明特征图中太过相近的值其实是差不多的，也可以说是冗余的，因此去掉也无所谓。

这种方法能帮我们提取到主要特征

两种池化方式：

加入池化后输出图片的尺寸计算：

与用步长进行计算其实是相似的，就是把步长替换为了池化尺寸。

池化的好处：

（1）最大池化提取纹理特征
（2）平均池化保留背景特征
（3）感受野增大
（4）经过池化操作以后，参数变少了
当然也有论文说取消池化层对于最终结果没有影响。

多通道多核卷积

通道：

比如rgb颜色，每个像素上多有三种颜色相加而得，那就称有三通道。

而特征图的通道由卷积核决定，每个卷积核能卷出一张特征图出来，那么有几个特征核就有几个通道

多输入通道计算过程：

输出只有一个通道的情况：

下图扩展为输出有三种的情况：

输出后的特征图为：

批量操作：

过拟合与欠拟合

泛化能力：

因此训练误差并不是越小越好。

过拟合

训练数据与过拟合：

正则项

这里引入一个范数的概念：

最终的损失函数为：

卷积神经网络的实现：

用卷积核数量改变层数，用池化改变特征图大小

将特征图卷小后就可以平铺展开，在进行回归。

计算loss

首先要转化为概率分布

然后计算交叉熵损失

下面是一个用来理解多分类公式的实例：

卷积神经网络的发展：

一些可以提出的创新点：

drop out

使某些节点在训练时不发挥作用，可以避免过拟合，减小计算量。

归一化：

经典模型AlexNet的解析：

AlexNet

注：Pool中的第一个数字表示单次池化范围，第二个数字表示池化步长

参考代码：

class MyAlexNet(nn.Module):                         #定义模型中样式
    def __init__(self):
        super(MyAlexNet, self).__init__()
        self.relu = nn.ReLU()
        self.drop = nn.Dropout(0.5)

        self.conv1 = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=11, stride=4,padding=2)
        self.pool1 = nn.MaxPool2d(3, stride=2)
        self.conv2 = nn.Conv2d(64,192,5,1,2)
        self.pool2 = nn.MaxPool2d(3, stride=2)

        self.conv3 = nn.Conv2d(192,384,3,1,1)

        self.conv4 = nn.Conv2d(384,256,3,1,1)

        self.conv5 = nn.Conv2d(256, 256, 3, 1, 1)

        self.pool3 = nn.MaxPool2d(3, stride=2)
        self.adapool = nn.AdaptiveAvgPool2d(output_size=6)

        self.fc1 = nn.Linear(9216,4096)

        self.fc2 = nn.Linear(4096,4096)

        self.fc3 = nn.Linear(4096,1000)

    def forward(self,x):                        #使用样式构造模型

        x = self.conv1(x)
        x = self.relu(x)
        x = self.pool1(x)

        x = self.conv2(x)
        x = self.relu(x)
        x = self.pool2(x)


        x = self.conv3(x)
        x = self.relu(x)
        print(x.size())
        x = self.conv4(x)
        x = self.relu(x)
        print(x.size())
        x = self.conv5(x)
        x = self.relu(x)
        x = self.pool3(x)
        print(x.size())
        x= self.adapool(x)
        x = x.view(x.size()[0], -1)

        x = self.fc1(x)
        x = self.relu(x)

        x = self.fc2(x)
        x = self.relu(x)

        x = self.fc3(x)
        x = self.relu(x)

        return x

AlexNet的创新点：

采用非饱和神经元（ReLU Nonlinearity）

在多个GPU上训练

为了在深层网络中训练120万张高分辨率图像，用两个 GPU 把网络给分开，形成上下两层。一部分参数和计算在第一块显卡上进行，另一部分参数在第二块显卡进行。
重叠池化

整体架构
整体架构
该网包含八层，前五个是卷积层，其余三个是全连接层，最后一个全连接层的输出作为softmax 函数的输入，输出超过 1000 个类别标签的分布。网络的输入为 150528维向量（224 × 224 × 3）

VGGNet

VggNet模型共有6种模型可选择（A到E），模型的区别主要在于卷积层，即每层stack

Vgg的创新点：

更小的卷积核：

在拥有相同的感受野的情况下可以保证参数更少

左边使用5*5的卷积核，参数量为25；右边使用两个3*3的卷积核，参数量为18

1*1卷积核

1*1卷积核可以用来降维，因为：

假设输入特征图的尺寸为 H×W×Cin，其中 H 是高度，W 是宽度，Cin 是输入通道数。使用 N 个1×1卷积核进行卷积操作，每个卷积核的大小为 1×1×Cin。经过卷积后，输出特征图的尺寸为 H×W×N。

当 N<Cin 时，就实现了降维操作。这是因为通过1×1卷积核的线性组合，将输入的 Cin 个通道映射到了 N 个通道，减少了特征图的通道数量。

采用了带动量的随机梯度下降

预初始化

先训练级别简单（浅层）的 𝑉𝐺𝐺 的 𝐴 模型（11层）作为预训练。然后用训练好的 𝐴 模型的权重去初始化后面更深的模型，加快训练的收敛速度

具体做法是：用网络 𝐴 模型前四个卷积层和最后三个全连接层参数的作为初始化参数

注意：比 𝐴 模型多余的层初始化仍采用随机初始化：均值 0，方差0.01 的正态分布；偏置初始化为 0

数据增强：

就是将图片先做各种预处理，增强模型在不同场景下识别图形的能力。

两种方法：单尺度和多尺度

在单尺度训练中，原图的短边被固定为一个固定值 𝑆 ，然后等比例缩放图片（正方形）。再从缩放的图片中裁剪 224 × 224 的子图用于训练模型

第二种方法是多尺度训练，即每个训练图像是独立随机地从 [𝑆𝑚𝑖𝑛 = 256, 𝑆𝑚𝑎𝑥 = 512]范围中随机抽样 𝑆 进行重新缩放

在多尺度训练中，每张图的短边随机为 256 到 512 之间的一个随机值，然后再从缩放的图片中随机裁剪 224 × 224 的子图

结论

更深的模型，效果更好（模型由A到E逐步加深，通过对比可得）

深层模型的泛化能力更好

参考代码：

class vggLayer(nn.Module):
    def __init__(self,in_cha, mid_cha, out_cha):
        super(vggLayer, self).__init__()
        self.relu = nn.ReLU()
        self.pool = nn.MaxPool2d(2)
        self.conv1 = nn.Conv2d(in_cha, mid_cha, 3, 1, 1)
        self.conv2 = nn.Conv2d(mid_cha, out_cha, 3, 1, 1)

    def forward(self,x):
        x = self.conv1(x)
        x= self.relu(x)
        x = self.conv2(x)
        x = self.relu(x)
        x = self.pool(x)
        return x

ResNet

相当震撼的论文，详细解读放在另一篇帖子里了。

CAU人工智能class6 ResNet

残差链接的作用：避免梯度消失

梯度消失：里层的参数计算梯度时是多次求偏导的结果，当偏导小于1时会越乘越小，最后趋近于0，为了避免这种情况采用f(x) + x的形式可以保证求偏导的结果至少大于1.

这也是为什么relu比sigmoid好的原因：

在右端sigmoid的梯度已经接近于0了

1乘1卷积：

作用1：降低参数，减小计算量

原参数：256 * 256 * 3 * 3

降维后参数：256 * 64 * 1 * 1+ 64 * 64 * 3 * 3 + 64 * 256 * 1 * 1

作用2：解决残差链接中输入输出特征图维度不同的问题：

总结一下卷积神经网络的主要模块：

代码展示：

import numpy as np
import paddle as paddle
import paddle.nn as nn
import paddle.nn.functional as F
from PIL import Image
import matplotlib.pyplot as plt
import os
print("本教程基于Paddle的版本号为："+paddle.__version__)

from paddle.vision.transforms import Compose, Normalize
transform = Compose([Normalize(mean=[127.5], std = [127.5], data_format = 'CHW')])
print('下载并加载训练数据')
train_dataset = paddle.vision.datasets.MNIST(mode = 'train', transform = transform)
test_dataset = paddle.vision.datasets.MNIST(mode = 'test', transform = transform)

#看看数据长什么样子
train_data0, train_label_0 = train_dataset[0][0], train_dataset[0][1]
train_data0 = train_data0.reshape([28, 28])
plt.figure(figsize = (2,2))
print(plt.imshow(train_data0, cmap = plt.cm.binary))
print('train_data0的标签为：' + str(train_label_0))

#定义多层感知机模型
class mnist(paddle.nn.Layer):
    def __init__(self):
        super(mnist,self).__init__()
        self.fc1 = nn.Linear(in_features = 28 * 28, out_features = 100)
        self.fc2 = nn.Linear(in_features = 100, out_features = 100)
        self.fc3 = nn.Linear(in_features = 100, out_features = 10)

    def forward(self, input_):
        x = paddle.reshape(input_, [input_.shape[0], -1])
        x = self.fc1(x)
        x = F.relu(x)
        x = self.fc2(x)
        x = F.relu(x)
        x = self.fc3(x)
        y = F.softmax(x)
        return y

from paddle.metric import Accuracy

model = paddle.Model(mnist())

optim = paddle.optimizer.Adam(learning_rate = 0.001, parameters = model.parameters())

model.prepare(optim, paddle.nn.CrossEntropyLoss(), Accuracy())

model.fit(train_dataset,test_dataset,epochs = 2, batch_size = 64, save_dir = 'multilayer_perception', verbose = 1)

#模型预测
test_data0, test_label_0 = test_dataset[0][0], test_dataset[0][0]
test_data0 = test_data0.reshape([28, 28])
plt.figure(figsize = (2,2))

print(plt.imshow(test_data0, cmap = plt.cm.binary))
print('test_data0的标签为：' + str(test_label_0))
#模型预测
result = model.predict(test_dataset, batch_size = 1)
#打印模型预测结果
print('test_data0 预测的数值为：%d' % np.argsort(result[0][0])[0][-1])