“90岁奶奶都能学会！DeepSeek本地部署教程”！！！

一、DeepSeek简介

DeepSeek是一种基于深度学习的语义搜索技术，能够高效处理非结构化数据并实现精准搜索。它广泛应用于知识管理、企业内搜索和智能客服等场景。

主要特点：

• 高精度语义搜索： 能够理解用户搜索意图并提供精准的结果。

• 可定制化： 支持根据场景调整模型参数与训练数据。

• 支持多种数据类型： 文本、图片、语音等。

• 技术红利:Deepseek开源免费，本地部署无成本，小白也能上手。

• 优势:隐私安全+离线运行

二、部署前的准备工作

在开始部署之前，需要完成以下准备工作：

1. 系统要求

• 操作系统： Linux（推荐Ubuntu 20.04）或Windows 10/11。

• 建议硬件配置：

  • CPU：Intel i5或以上

  • 内存：16GB及以上

  • 显卡：NVIDIA GPU 8GB以上

  • 存储空间：至少50GB （建议固态硬盘）

2. 软件环境

• Python版本： Python 3.8或更高。

• 需要配置好python环境变量。

3.安装部署

(以windows10为例)

1、下载ollama 下载链接：Download Ollama on Windows

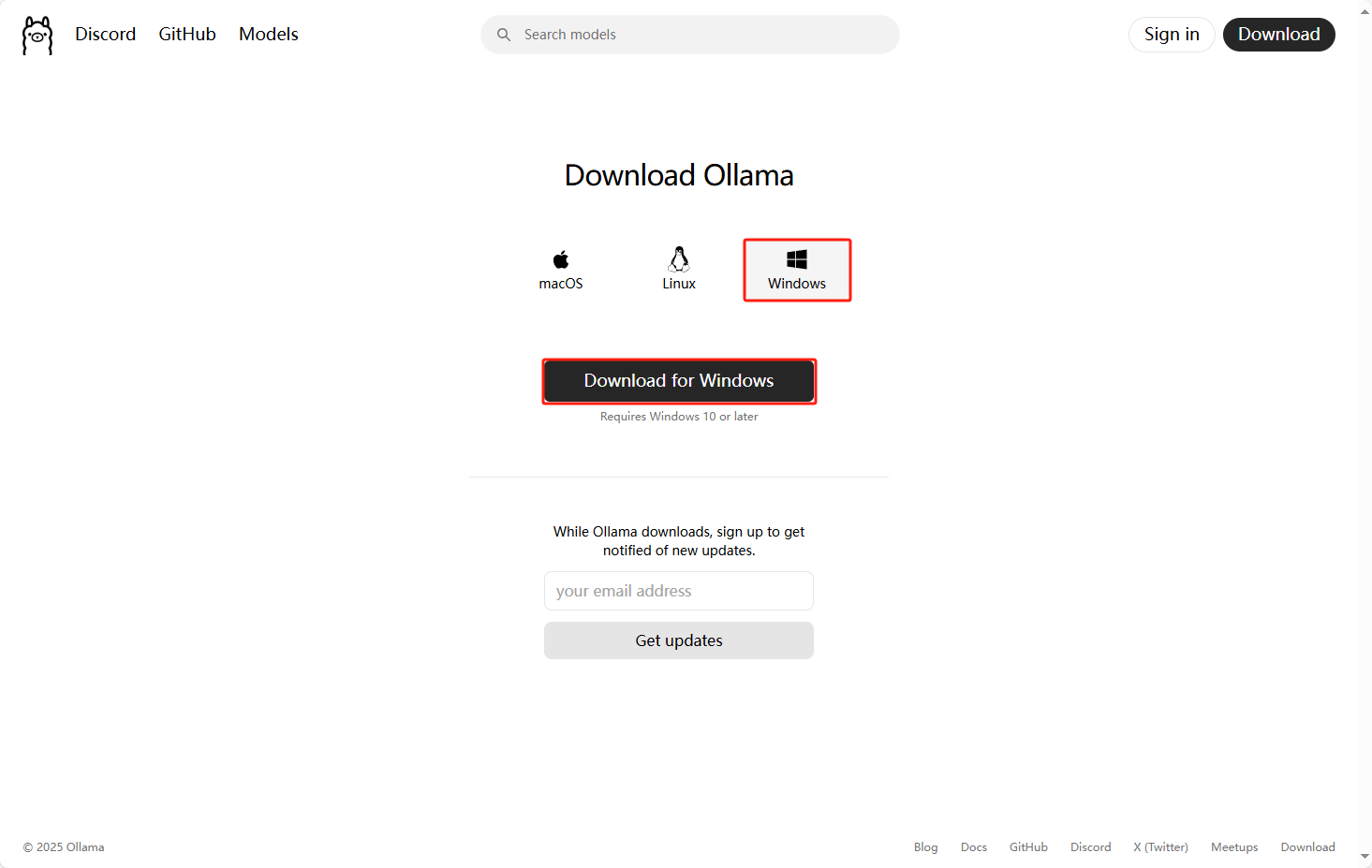
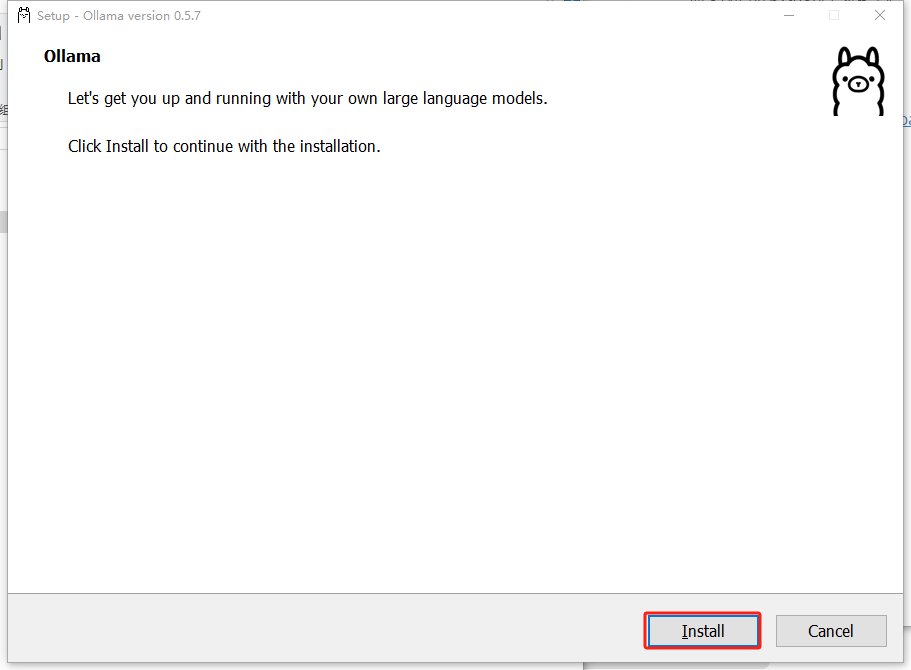
验证ollama是否安装完成

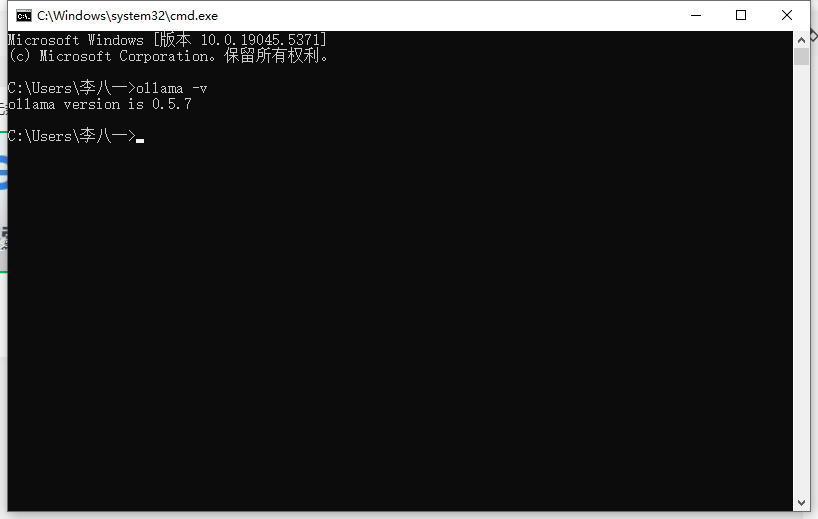
2、下载deepseek运行

ollama run deepseek-r1:32b
注意:deepseek有多种版本，我这里用的32b，部署方法一样

3、效果展示 

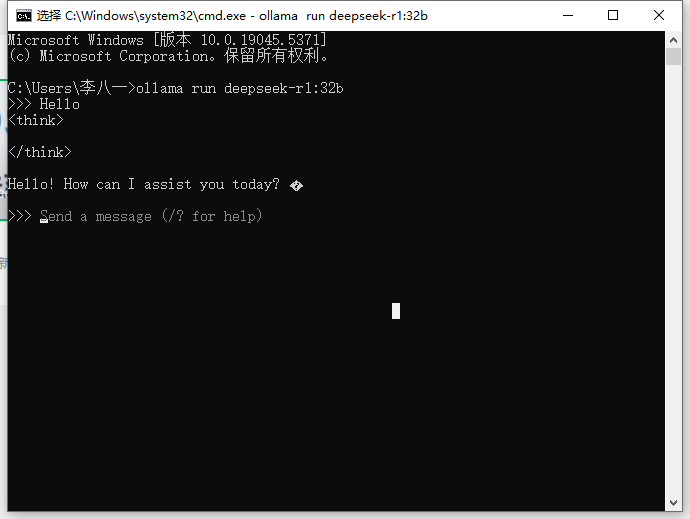
4、搭配web界面

open-webui,本地大语言模型运行框架。

pip install open-webui
#下载open-webui(需要提前配置好python环境变量)
open-webui serve
#启动open-webui(本地需要提前将大模型跑起来)

浏览器访问：http://localhost:8080

第一次访问需要创建一个账号 效果如图：
 

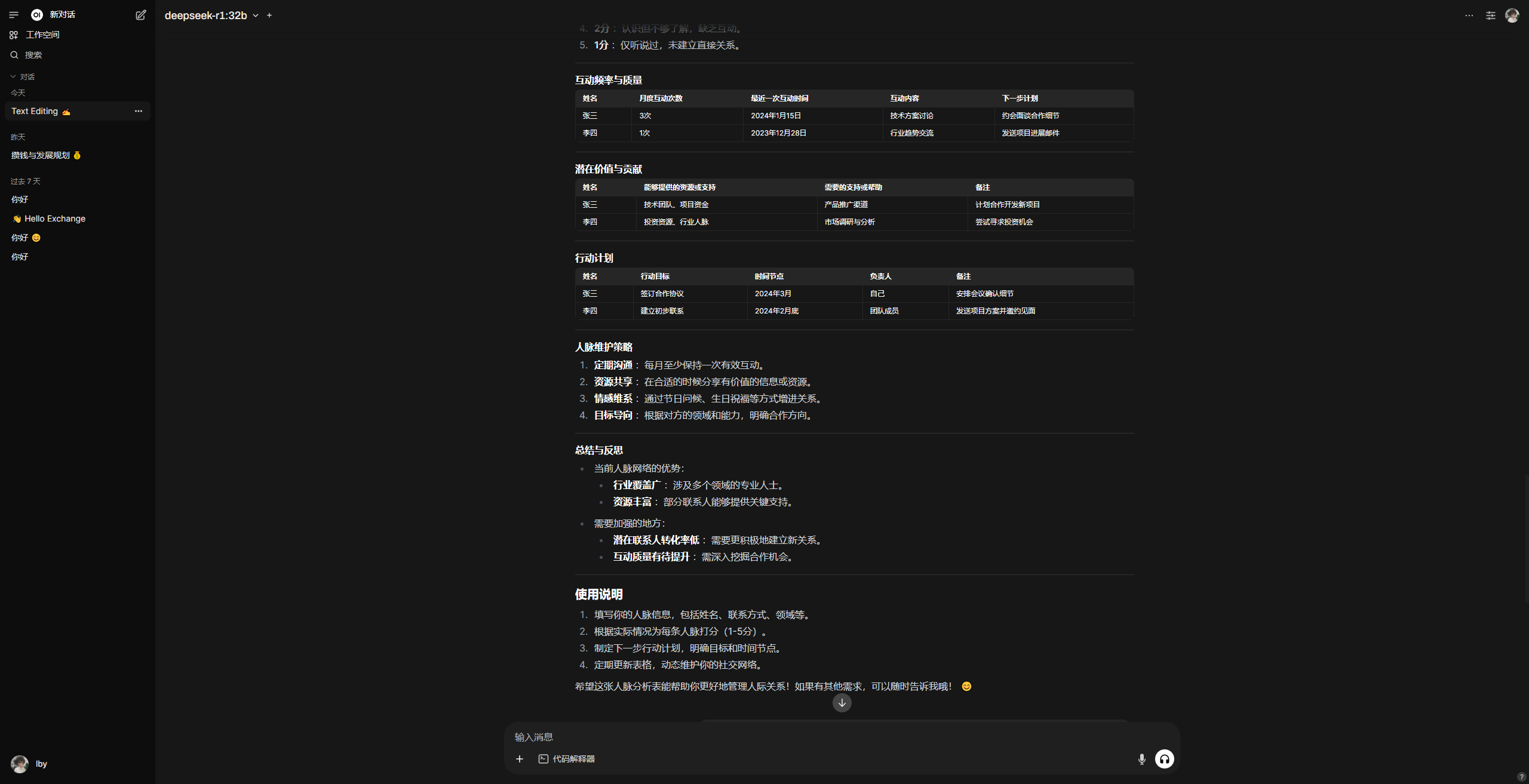
来源与微信公众号：太白也无奈