一、MATLAB内置求解方程函数
1.roots(多项式函数)
求 ![]() 的根
的根
p=[1,-3,1];
x=roots(p)2.fzero(非线性方程)
求 ![]() 的根
的根
x=-5:0.1:5;
y1=x.*x-3*x+1;
y2=zeros(size(x));
plot(x, y1, x, y2);
f=@(x) x*x-3*x+1;
x1=fzero(f, 0.5)
x2=fzero(f, 2.5)
3.fsolve(非线性方程组)
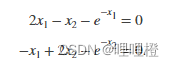
clc
clear all
x0 = [-5;-5];
[x,fval] = fsolve(@(x)(2*x(1)-x(2)-exp(-x(1)) -x(1)+2*x(2)-exp(-x(2))),x0)二、使用自编函数求解
主函数:
clc
clear all
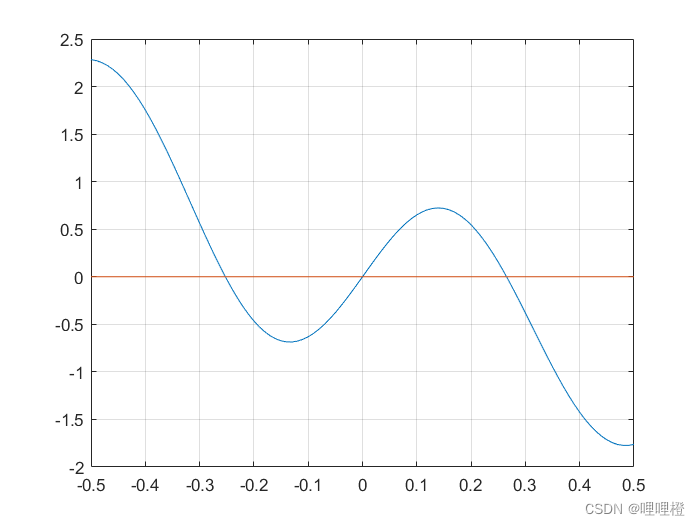
% 绘制函数图像
x=-0.5:0.01:0.5;
y1=sin(10*x)-x.*exp(-x)-x;
y2=zeros(size(x));
plot(x,y1,x,y2)
grid on;
% 多次画图,确定此函数有三个根,因函数非单调,划分为3个有根区间[-0.3,-0.2],[-0.1,0.1],[0.2,0.3]
% 用二分法求这三个区间的方程解
x1=dichotomy(-0.3,-0.2);
x2=dichotomy(-0.1,0.1);
x3=dichotomy(0.2,0.3);
% 用牛顿法求这三个区间的方程解
fun=inline('sin(10*x)-x.*exp(-x)-x');
dfun=inline('10*cos(10*x)-exp(-x)+x.*exp(-x)-1');
x1_1=newton(fun,dfun,-0.3,1.0e-8);
x2_1=newton(fun,dfun,-0.1,1.0e-8);
x3_1=newton(fun,dfun,0.2,1.0e-8);
% 用弦截法求这三个区间的方程解
x1_1_1 = secant_method(-0.3,-0.2);
x2_1_1 = secant_method(-0.1,0.1);
x3_1_1 = secant_method(0.2,0.3);子函数(二分法):
function root = dichotomy(a,b)
%root为二分法输出的根,输入的a,b为判断出的有根区间
% 误差精度要低于10^(-8);
accuracy=1.0e-8;
% 求根函数
f=@(x)sin(10*x)-x.*exp(-x)-x;
fa=f(a);% 计算左端点函数值
fb=f(b);% 计算右端点函数值
fmid=f((a+b)/2);% 计算中点函数值
% 判断函数情况,改变函数计算区间
% 使用递归方法
if(fa*fmid>0)
a_bis=(a+b)/2;
root=dichotomy(a_bis,b);
else
if(fa*fmid==0)
root=(a+b)/2;
else
if(abs(b-a)<=accuracy)
root=(a+b)/2;
else
b_bis=(a+b)/2;
root=dichotomy(a,b_bis);
end
end
end子函数(牛顿法):
function x = newton(fname,dfname,x0,e)
%fname为函数名,dfname为函数fname的导函数,x0为迭代初值
%e为精度,N为最大迭代次数(默认100)
%牛顿迭代法
N=100;
x=x0;
x0=x+2*e;
k=0;
while abs(x0-x)>e&&k<N
k=k+1;
x0=x;
x=x0-feval(fname,x0)/feval(dfname,x0);
end
if k==N
warning('已达最大迭代次数');
end子函数(弦截法:):
function root= secant_method(a,b)
%root为弦截法输出的根,k为迭代次数,输入的a,b为区间的两个节点
% 误差精度要低于10^(-8);
accuracy=1.0e-8;
% 本题求根函数
f=@(x) sin(10*x)-x.*exp(-x)-x;
% 计算左端点函数值
fa=f(a);
% 计算右端点函数值
fb=f(b);
%每一步弦截的跟
root=a-(b-a)*fa/(fb-fa);
% 初值准备,其中误差项error_term为1是为了之后进去while循环的初始条件
k=0;
error_term=0.1;
while((error_term>accuracy)&&(k<=300))
k=k+1;
x1=root;
fx=f(root);
%确定衰减方向,保证是往f减少出缩进
s=fx*fa;
if(s>0)
root=b-(x1-b)*fb/(fx-fb);
else
root=a-(x1-a)*fa/(fx-fa);
end
error_term=abs(root-x1);
end
end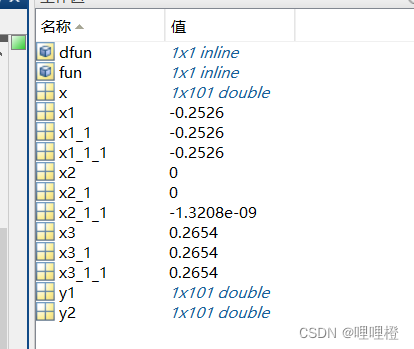







 本文介绍了MATLAB中的内置求解方程函数如roots、fzero和fsolve,以及如何使用自编函数实现二分法、牛顿法和弦截法来解决非线性方程。通过实例展示了如何在MATLAB中应用这些方法求解方程的根。
本文介绍了MATLAB中的内置求解方程函数如roots、fzero和fsolve,以及如何使用自编函数实现二分法、牛顿法和弦截法来解决非线性方程。通过实例展示了如何在MATLAB中应用这些方法求解方程的根。
















 489
489

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








