一、伪逆概述
并非所有矩阵都有逆矩阵。逆用于求解方程组,在某些情况下,方程组没有解,因此逆不存在。然而,找到一个最小化误差的近似值是有意义的。例如,使用伪逆找到一组数据点的最佳拟合线。
Moore-Penrose 伪逆是SVD的直接应用。
正如我们在之前篇章中看到的,矩阵A的逆矩阵可用于求解方程Ax=b:
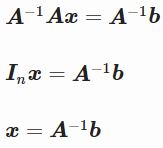
但是在方程组有0个或多个解的情况下,无法找到逆,也无法求解方程,这时候需要伪逆上场了。
伪逆记作![]() ,并
,并
并非所有矩阵都有逆矩阵。逆用于求解方程组,在某些情况下,方程组没有解,因此逆不存在。然而,找到一个最小化误差的近似值是有意义的。例如,使用伪逆找到一组数据点的最佳拟合线。
Moore-Penrose 伪逆是SVD的直接应用。
正如我们在之前篇章中看到的,矩阵A的逆矩阵可用于求解方程Ax=b:
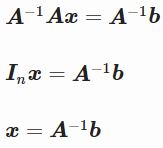
但是在方程组有0个或多个解的情况下,无法找到逆,也无法求解方程,这时候需要伪逆上场了。
伪逆记作![]() ,并
,并
 1106
1106

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


