9*9数独求解算法（C++）

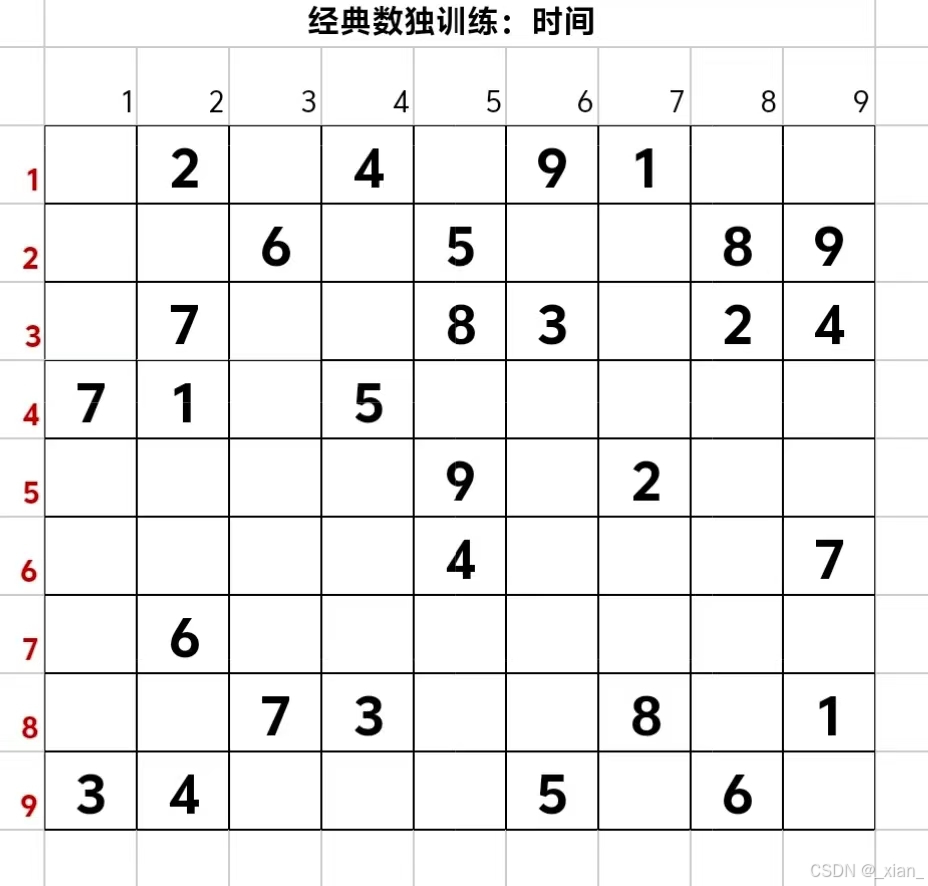
1.使用递归法实现回溯策略，依次对候选数（1-9）逐个进行合法性判定，完成数独

C++代码如下：

// 检查在 (row, col) 位置填入 num 是否合法
bool isSafe(int arr[9][9], int row, int col, int num) {
    // 检查行
    for(int i = 0; i < 9; i++) {
        if(arr[row][i] == num) return false;
    }
    // 检查列
    for(int i = 0; i < 9; i++) {
        if(arr[i][col] == num) return false;
    }
    // 检查九宫格
    int startRow = row - row % 3;
    int startCol = col - col % 3;
    for(int i = 0; i < 3; i++) {
        for(int j = 0; j < 3; j++) {
            if(arr[i + startRow][j + startCol] == num) return false;
        }
    }
    return true;
}

// 回溯法解决数独问题
bool solveSudoku(int arr[9][9]) {
    for(int row = 0; row < 9; row++) {
        for(int col = 0; col < 9; col++) {
            if(arr[row][col] == 0) {
                for(int num = 1; num <= 9; num++) {
                    if(isSafe(arr, row, col, num)) {
                        arr[row][col] = num;
                        if(solveSudoku(arr)) {
                            return true;
                        }
                        arr[row][col] = 0; // 回溯
                    }
                }
                return false; 
            }
        }
    }
    return true; 
}

2.尝试过程优化，先用行列与九宫格约束法把能确定的格子先填上，再对未填的格子执行回溯算法，

C++代码：

//列遍历
//参数: 1.当前所在行标, 2.记录已有的数的数组
void SudokuCols(const int arr[9][9], int row, int reArr[10]) {
	for(size_t i = 0; i < 9; i++) {
		reArr[arr[row][i]] = 0;
	}
}
//行遍历
//参数: 1.当前所在列标, 2.记录已有的数的数组
void SudokuRows(const int arr[9][9], int col, int reArr[10]) {
	for(size_t i = 0; i < 9; i++) {
		reArr[arr[i][col]] = 0;
	}
}
//获取标识可直接计算的位置的数组
//参数：1.数独数组，2.要计算的二维数组, 3.存储已有的数的数组, 4.行标  5.列标
void getPointArr(const int arr[9][9], int PointArr[9][9], const int reArr[10], int row, int col) {
	int couts = 0;
	for(size_t i = 1; i < 10; i++) {
		reArr[i] == 1 && couts++;
	}
	if(couts == 1 && arr[row][col] == 0) {
		PointArr[row][col] = 1;
	}
}
//获取九宫格有几个数
//参数：1.数独数组 2.行坐标 3.列坐标 4.记录已有的数的数组
void get9BoxGrid(const int arr[9][9], int row, int col, int reArr[10]) {
	int startRow = row - row % 3;
	int startCol = col - col % 3;
	for(int i = 0; i < 3; i++) {
		for(int j = 0; j < 3; j++) {
			reArr[arr[i + startRow][j + startCol]] = 0;
		}
	}
}
// 检查在 (row, col) 位置填入 num 是否合法
bool isSafe(int arr[9][9], int row, int col, int num) {
	// 检查行
	for(int i = 0; i < 9; i++) {
		if(arr[row][i] == num) return false;
	}
	// 检查列
	for(int i = 0; i < 9; i++) {
		if(arr[i][col] == num) return false;
	}
	// 检查九宫格
	int startRow = row - row % 3;
	int startCol = col - col % 3;
	for(int i = 0; i < 3; i++) {
		for(int j = 0; j < 3; j++) {
			if(arr[i + startRow][j + startCol] == num) return false;
		}
	}
	return true;
}
//解部分数独函数  
void getPortionSudoku(int arr[9][9]) {
	int reArr[10] = { 1 };

	int PointArr[9][9] = { 0 };

	bool stop = false;

	while(!stop) {
		stop = true;
		memset(PointArr, 0, sizeof(PointArr));
		for(int i = 0; i < 9; ++i) {
			for(int j = 0; j < 9; ++j) {
				fill(reArr, reArr + 10, 1);
				//获取行列已有的数
				SudokuCols(arr, i, reArr);
				SudokuRows(arr, j, reArr);
				//获取能计算确定的数的位置数组
				getPointArr(arr, PointArr, reArr, i, j);
				//按行列判定法计算填入数字
				if(PointArr[i][j]) {
					for(size_t num = 1; num < 10; num++) {
						if(reArr[num]) {
							arr[i][j] = num;
							stop = false;
							break;
						}
					}
				} else {//按九宫格判定法计算填入数字
					if(arr[i][j] == 0) {
						int nineBoxGrid[9] = { 0 };
						get9BoxGrid(arr, i, j, reArr);
						getPointArr(arr, PointArr, reArr, i, j);
						if(PointArr[i][j]) {
							for(size_t num = 1; num < 10; num++) {
								if(reArr[num]) {
									arr[i][j] = num;
									stop = false;
									break;
								}
							}
						}
					}
				}
			}
		}
	}
}
// 回溯法解决数独问题
bool solveSudoku(int arr[9][9]) {
	for(int row = 0; row < 9; row++) {
		for(int col = 0; col < 9; col++) {
			if(arr[row][col] == 0) {
				for(int num = 1; num <= 9; num++) {
					if(isSafe(arr, row, col, num)) {
						arr[row][col] = num;
						if(solveSudoku(arr)) {
							return true;
						}
						arr[row][col] = 0; // 回溯
					}
				}
				return false;
			}
		}
	}
	return true;
}

提供main函数：

int main() {
	int arr[9][9] = {
		{ 0, 2, 0, 4, 0, 9, 1, 0, 0 },
		{ 0, 0, 6, 0, 5, 0, 0, 8, 9 },
		{ 0, 7, 0, 0, 8, 3, 0, 2, 4 },
		{ 7, 1, 0, 5, 0, 0, 0, 0, 0 },
		{ 0, 0, 0, 0, 9, 0, 2, 0, 0 },
		{ 0, 0, 0, 0, 4, 0, 0, 0, 7 },
		{ 0, 6, 0, 0, 0, 0, 0, 0, 0 },
		{ 0, 0, 7, 3, 0, 0, 8, 0, 1 },
		{ 3, 4, 0, 0, 0, 5, 0, 6, 0 }
	};

	int rows = sizeof(arr) / sizeof(arr[0]);
	int cols = sizeof(arr[0]) / sizeof(arr[0][0]);

	for(int i = 0; i < rows; ++i) {
		for(int j = 0; j < cols; ++j) {
			cout << arr[i][j] << " ";
		}
		cout << endl;
	}
	cout <<"计算后："<< endl;

	getPortionSudoku(arr);

	if(solveSudoku(arr)) {
		for(int i = 0; i < 9; i++) {
			for(int j = 0; j < 9; j++) {
				cout << arr[i][j] << " ";
			}
			cout << endl;
		}
	} else {
		cout << "No solution exists" << endl;
	}

	return 0;
}