机器视觉学习——相机成像模型

相机成像模型

        相机成像的过程其实就是将现实中的物体映射到成像平面，再将坐标转换为像素坐标的过程。本质上，相机成像模型可以简化为小孔成像模型。

         将相机成像过程简化，假设在空间中存在一点， 点在成像平面内映射的点为点，相机成像模型的目标就是求解成像平面中 的坐标。考虑到坐标，就要讨论与相机成像模型相关的四个坐标系以及它们之间坐标的转换关系。

世界坐标系到相机坐标系

         坐标系之间的坐标变换为刚体变换，物点位置由世界坐标系到相机坐标系的变换过程如下图所示：

            点从世界坐标经过旋转矩阵 和平移矩阵 可以转换为相机坐标，公式为：

        使用齐次坐标，从而转换成矩阵的形式，即：

        称为相机外参矩阵，外参矩阵取决于相机坐标系和世界坐标系的相对位置。外参矩阵中，旋转矩阵为3×3的矩阵，使世界坐标系经过旋转后与相机坐标系的方向相同。有三个方向的旋转，分别为绕x轴转，绕y轴转，绕z轴转。其中、、为转轴旋转的角度。这些矩阵参数为：

相机坐标系到图像坐标系

        通过透视投影关系，利用相似的原理，从3D转换到2D。用来表示相距，投影过程如下图所示：

        根据相似三角形定理，可得：

        整理后可得：

        用齐次坐标，用矩阵表示坐标变换关系：

        在相机坐标系转换到图像坐标系的过程中，是由3维坐标转换为2维坐标的过程，因此，转换后的结果会损失相机和成像平面的距离信息。

图像坐标系到像素坐标系

        像素坐标系和图像坐标系都在成像平面上，但是原点所在位置不同，单位不同。图像坐标系的原点为相机光轴与成像平面的交点，即光心，通常情况下是成像平面的中点。图像坐标系的单位是，而像素坐标系的原点在图像左上角，单位是 。

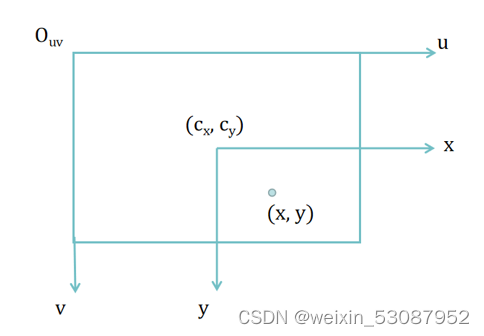
        在像素坐标系中，每个像素沿x轴的实际物理尺寸大小是，令；每y轴的实际物理尺寸大小是，令。两坐标系之间的单位关系为。由上图可知两个坐标系之间转换的关系式为：

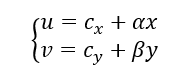
        通过齐次坐标，用矩阵表示坐标变换关系：

        式中表示为相机的内参矩阵，内参矩阵取决于相机的内部参数。通过上述三个坐标系的转换过程，即可获得现实世界空间点在成像平面的像素坐标。将成像过程的所有过程总结为一个式子，即：