相机的成像模型

大大大管的笔记本

已于 2024-05-09 16:43:10 修改

阅读量2.2k

点赞数 15

文章标签：数码相机计算机视觉人工智能图像处理 opencv 视觉检测

于 2024-02-06 16:54:05 首次发布

本文链接：https://blog.youkuaiyun.com/cg1135217680/article/details/136059411

版权

本文详细阐述了相机成像模型中的四个关键步骤：从世界坐标系到相机坐标系、相机坐标系到图像坐标系、图像坐标系到像素坐标系的转换，以及相机内参和外参矩阵在成像过程中的作用。特别强调了尺度因子在三维重建和视觉测量中的重要性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

相机成像模型

在学习计算机视觉的过程中，少不了接触针孔相机的成像模型，这是基础也是容易让人混淆的东西，特别是其中参数的概念，对应的物理意义是什么。其实，相机的成像模型无非就是几个坐标系的转换，其中涉及到的坐标系有：世界坐标系（world frame）、相机坐标系（camera frame）、图像坐标系（image frame）、像素坐标系（pixel frame）。其中，图像坐标系与像素坐标系为二维坐标系，像素坐标系通常以图像的左上角为坐标原点。

下面我将会分为4个部分讲述他们的关系。

1.世界坐标系与相机坐标系的转换

所谓世界坐标系就是世界上任意一个地方都可以成为一个坐标系。假设在空间中存在一个点称为 $P^{W}$ ，那么世界坐标系在不同的位置， $P^{W}$ 的坐标自然也就不同。

现在固定一个世界坐标系， $P^{W}$ 的坐标自然也就固定不变了。比如，在相机标定的过程中，就是假设世界坐标系在标定板（棋盘格）的左上顶点处；在视觉测量的过程中，通常以被测物体作为世界坐标系，有时也被称为物体坐标系。

下面涉及到一些刚体变换的知识。设 $R$ 、 $T$ 分别为世界坐标系到相机坐标系的旋转变换和平移变换， $P^{C}$ 为相机坐标系下的坐标。那么 $P^{W}$ 到 $P^{C}$ 的转换关系为：

$P^{C}=\begin{bmatrix}R&T & \\ 0 &\mathbf{ 1} \end{bmatrix}P^{W}$

注意，这里 $P^{C}$ 和 $P^{W}$ 都变为齐次坐标，也就是多加了一个1，例如： $P^{C}$ 表现形式为 $[X^{C}, Y^{C}, Z^{C}, 1]^{T}$ 。

2.相机坐标系与图像坐标系的转换

将世界坐标系转换到相机坐标系后，原来的 $P^{W}$ 也就变为 $P^{C}$ 了。在拍摄过程中， $P^{C}$ 会投影到CCD或CMOS传感器上，成为一个像素点，该像素点在图像坐标系下的坐标为 $p^{i}=(x, y)$ ，下图可以简述其中的关系。

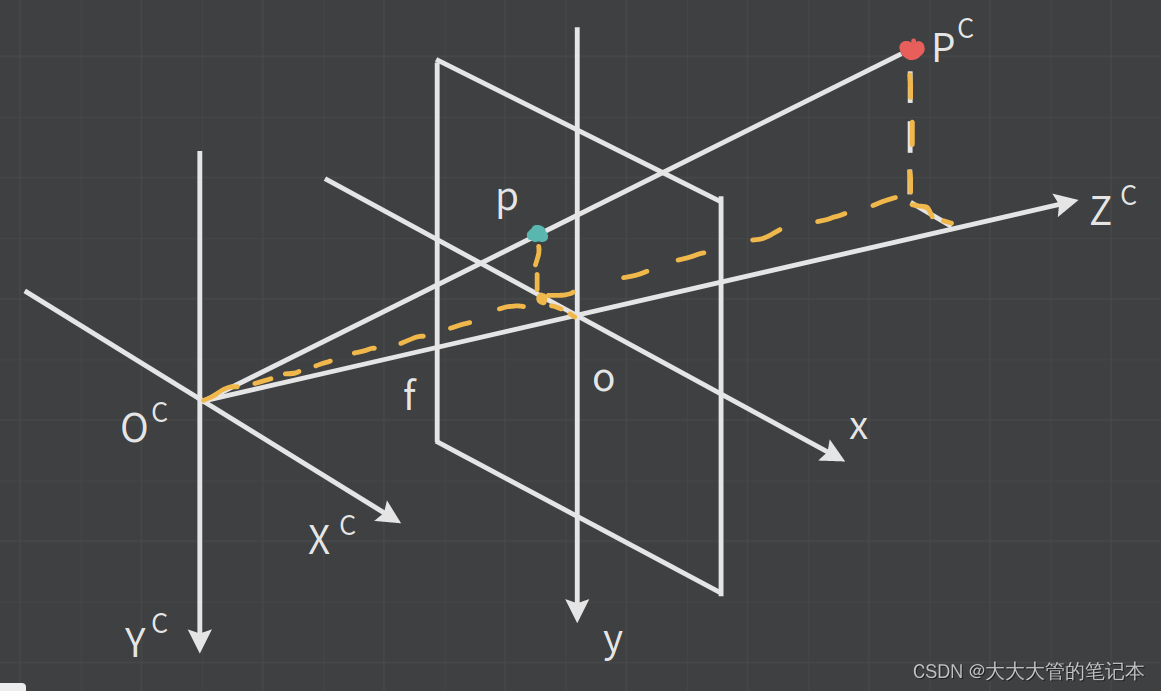
而投影也是一种比例关系或者说是相似关系，如下：

$x=\frac{X^{C}f}{Z^{C}}$ 和 $y=\frac{Y^{C}f}{Z^{C}}$

矩阵化之后为：

$\begin{bmatrix} x\\ y \\ 1 \end{bmatrix}=\frac{1}{Z^{C}}\begin{bmatrix} f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0 & 1& 0 \end{bmatrix}\begin{bmatrix} X^{C}\\ Y^{C}\\ Z^{C}\\ 1 \end{bmatrix}$

3.图像坐标系与像素坐标系的转换

完成上面两个关系后，只需要获得图像坐标系与像素坐标系的转换关系，就可以将世界坐标系下的点投影转换为像素坐标系下了（为什么要转换到像素坐标系呢？因为通常像素点的坐标指的就是像素坐标系下的坐标，而不是图像坐标系下的坐标）。而图像坐标系与像素坐标系均为二维平面，将两个二维平面平铺之后，它们之间的关系如下图所示：

设 $o$ 点在像素坐标系下的坐标为 $(u_{0}, v_{0})$ ，这两个点通常也被成为主点坐标（principal point），也就是相机坐标系的Z轴与图像平面的交点。由于CCD或CMOS的传感器通常不为正方形，故设像元的横向尺寸和纵向尺寸分别为 $dx$ 和 $dy$ ，其单位则为 $mm/pixel$ 。

将实际的空间点离散化为相机的像素值（在实际编程的时候 $x$ 和 $y$ 可能为小数，需要取整），有：（注意：在部分参考资料中还加入了倾斜因子，该值通常较小，这里就省略了）

$u=\frac{x}{dx}+u_{0}$

$v=\frac{y}{dy}+v_{0}$

将上面的等式转换为矩阵形式并且升一个维度变为齐次形式，有：

$\begin{bmatrix} u\\ v \\ 1 \end{bmatrix}=\begin{bmatrix} \frac{1}{dx} & 0 &u_0 \\ 0 & \frac{1}{dx} & v_0\\ 0& 0 & 1 \end{bmatrix}\begin{bmatrix} x\\y \\1 \end{bmatrix}$

4.成像模型

将上面三个矩阵依次相乘，则有：

$Z^{C}\begin{bmatrix} x\\ y \\ 1 \end{bmatrix}=\begin{bmatrix} \frac{1}{dx}& 0& u_0\\ 0& \frac{1}{dy}& v_0\\ 0& 0& 1\\ \end{bmatrix}\begin{bmatrix} f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0 & 1& 0 \end{bmatrix}\begin{bmatrix} R & T\\ 0& \mathbf{1} \end{bmatrix}\begin{bmatrix} X^{W}\\ Y^{W}\\ Z^{W}\\ 1 \end{bmatrix}$

其中，坐标两个矩阵只与相机的参数相关，故也被称为相机内参矩阵 $K$ 。中间包含 $R$ 、 $T$ 的矩阵是世界坐标系到相机坐标系的变换矩阵，也被称为外参矩阵。 $Z^{C}$ 则是一个很重要，也很神奇的参数，在部分参考资料会将它写成 $s$ ，称为尺度因子。这个参数在三维重建、视觉测量等领域都非常重要。

根据上面的解释，我们可以把上式简化成：

$s\begin{bmatrix} u\\ v\\ 1 \end{bmatrix}=K\begin{bmatrix} R & T\\ 0&\boldsymbol{1} \end{bmatrix}\begin{bmatrix} X^{W}\\ Y^{W}\\ Z^{W}\\ 1 \end{bmatrix}$

其中

$K=\begin{bmatrix} \frac{f}{dx} & 0& u_0& 0\\ 0& \frac{f}{dy}& v_o& 0\\ 0& 0& 1& 0 \end{bmatrix}=\begin{bmatrix} f_x & 0& u_0& 0\\ 0& f_y& v_0& 0\\ 0& 0& 1& 0 \end{bmatrix}$

在部分资料中会将 $\begin{bmatrix} R & T\\ 0&\boldsymbol{1} \end{bmatrix}$ ，改写为 $\begin{bmatrix} R & T\end{bmatrix}$ 。故也写作

$Z^{C}\begin{bmatrix} x\\ y \\ 1 \end{bmatrix}=\begin{bmatrix} \frac{1}{dx}& 0& u_0\\ 0& \frac{1}{dy}& v_0\\ 0& 0& 1\\ \end{bmatrix}\begin{bmatrix} f& 0& 0\\ 0& f& 0\\ 0& 0 & 1\end{bmatrix}\begin{bmatrix} R & T\\ \end{bmatrix}\begin{bmatrix} X^{W}\\ Y^{W}\\ Z^{W}\\ 1 \end{bmatrix}$