深度学习学习笔记（二）

weixin_51431157

已于 2023-03-30 19:11:32 修改

阅读量160

点赞数

分类专栏：吴恩达深度学习文章标签： python 机器学习深度学习

于 2023-03-01 21:43:53 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_51431157/article/details/129277771

版权

吴恩达深度学习专栏收录该内容

8 篇文章

订阅专栏

第一门课第二周

文章目录

神经网络的编程基础
一、二分类(Binary Classification)
二、逻辑回归(Logistic Regression)
三、逻辑回归的代价函数（Logistic Regression Cost Function）
四、梯度下降法（Gradient Descent）--梯度消失(梯度弥散)、梯度爆炸
五、m 个样本的梯度下降
六、logistic 损失函数的解释
总结

一、二分类

举一个简单的猫识别例子：输入一张图片，如果通过算法识别这张图片有猫，则输出y=1，若识别结构结果不是猫，则输出y=0。

输入一张RGB图片（三个分别代表红绿蓝的矩阵，假设像素格式为5*4*3）

将图片的三个矩阵像素值转换为符合x输入的值（n行1列的向量）

训练集格式：

x: 输入数据，维度为（n,1） y:输出结果，取值为0或1

$X= [x^{(1)},x^{(2)},...,x^{(m)}]$ 表示所有的训练数据集的输入值,维度为n*m（m为样本数）

$Y= [y^{(1)},y^{(2)},...,y^{(m)}]$ 表示训练集的输出值，维度为1*m

二、逻辑回归

预测值yhat如何得到0或1的值？

采用sigmoid函数作为激活函数， $y\hat{} = g(z)$ , $g(z) = \frac{1}{1+e^{-z}}$ , $z = w^{T}*x + b$

当z非常大时，yhat=1;当z非常小时，yhat=0。

剩下所需做的是学习合适的参数w和b,使预测值yhat尽可能等于真实值y。

三、逻辑回归的代价函数

损失函数又叫做误差函数，衡量预测输出值和实际值有多接近,用来衡量算法的运行情况

$L(y\hat,y) = -ylog(y\hat)-(1-y)log(1-y\hat)$

以上为单个样本的损失函数，在m个样本上需要求对m的平均，得到代价函数J

为什么不使用平方差来表示损失函数？

因为大多数情况下可能有多个局部最优，而不是有一个全局最优

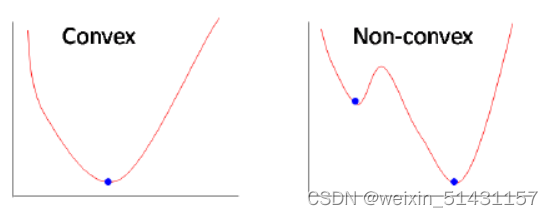
凸函数条件：损失函数两阶导数大于等于零在定义域内恒成立，经对两损失函数求导可得平方差损失函数为非凸，log损失函数为凸函数，具体求导步骤可参考：为什么不用平方误差（MSE）作为Logistic回归的损失函数？_为什么逻辑回归不能用mse_拉风小宇的博客-优快云博客

当y=1时，单个样本损失函数为L=-log(yhat),要使得L尽可能小，则需要yhat尽可能大，由sigmoid函数可知，yhat会接近于1；若预测错误，yhat预测为0，则损失L趋于无穷大，会极大地惩罚错误分类，而平方差预测错误的损失较小，惩罚力度较小。

当y=0时，单个样本损失函数为L=-log(1-yhat),要使得L尽可能小，则需要yhat尽可能小，由sigmoid函数可知，yhat会接近于0；同理，预测错误时，平方差损失函数惩罚力度小。

四、梯度下降法

原理：一种优化算法，该算法从任一点开始，沿该点梯度的反方向（梯度方向为导数上升的方向）运动一段距离，再沿新位置的梯度反方向运行一段距离 ...... 如此迭代。解一直朝下坡最陡的方向运动，希望能运动到函数的全局最小点。

目的：在你测试集上，通过最小化代价函数（成本函数）𝐽(𝑤, 𝑏)来训练的参数𝑤和b

（找到代价函数J位于最低点对应的参数w和b）

采用随机初始化的方法来初始化参数𝑤和b

梯度下降的步骤是在初始点按照曲线上最陡峭的方向迭代，直至最低点（即对应全局最优解）

下图迭代四次至最优解

参数w和b的更新：
假定在二维空间内，横轴表示w,纵轴表示J(w)， $\frac{\partial J}{\partial w}$ 表示向下走的长度,引入学习率 $\alpha$ （控制步长，表示迭代的快慢），迭代公式为

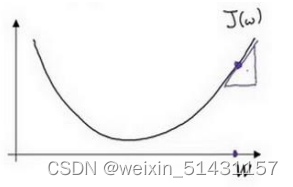
对参数b同理，迭代公式为：

梯度消失(梯度弥散)、梯度爆炸

靠近输出层的隐藏层梯度大（梯度下降的步骤是在初始点按照曲线上最陡峭的方向迭代，直至最低点），参数更新快，所以很快就会收敛;
靠近输入层的隐藏层梯度小，参数更新慢，几乎就和初始状态一样，随机分布。

梯度消失(梯度弥散)、梯度爆炸产生原因：激活函数导数与权重m的累乘

如果权重w设置的过大，随着网络层数的不断加深，最终梯度将以指数形式增加（梯度爆炸）
如果激活导数值小于1，随着网络层数的不断加深，最终梯度将以指数形式减少（梯度消失）

梯度消失与梯度爆炸_zxucver的博客-优快云博客

五、m个样本的梯度下降

需要使用到两个for循环来实现（1.遍历m个样本；2.遍历所有特征值（w1,w2,w3...wn））

z = 0   #初始化z为0
for i in range(n_x)：   #n_x个特征w    
    z += w[i]*x[i]
z += b

这样显示的for对算法很低效，向量化的技术解决for循环

z = np.dot(w,x) + b

实验两种方法对维度为（1000000,1）的两个向量的乘法运算：

import random
import time
import numpy as np
a = np.array([1,2,3,4,5,6,7,8,9,10])
print(a)
a = np.random.rand(1000000)
b = np.random.rand(1000000)

tic = time.time()
#向量化
c = np.dot(a,b)
toc = time.time()
print('向量化运算时间为'+str(1000*(toc - tic))+'ms')

#显式for循环
c = 0
tic = time.time()
for i in range(1000000):
    c += a[i] * b[i]
toc = time.time()
print('for循环运算时间' + str(1000*(toc - tic)) + 'ms')

[ 1  2  3  4  5  6  7  8  9 10]
向量化运算时间为0.9987354278564453ms
for循环运算时间402.22883224487305ms

可见向量化运算比显示for循环运算快四百多倍

六、logistic 损失函数的由来

根据条件概率，即算法的输出𝑦^（预测值）是给定训练样本 𝑥 条件下 𝑦 等于 1 的概率P（y|x）=y^,

则定训练样本 𝑥 条件下 𝑦 等于 0 的概率P（y|x）=1 - y^

合并得：

取对数得：-L(y^,y) = ylog(y^) + (1-y)log(1-y^)

因为要最小化代价函数，所以加上负号，得：L(y^,y) = -ylog(y^) - (1-y)log(1-y^)

总结

1、平方误差（MSE）的损失函数不是凸函数，log损失函数为凸函数。

2、梯度下降的步骤是在初始点按照曲线上最陡峭的方向迭代，直至最低点。

3、通过 numpy 内置函数和避开显式的循环(loop)的方式进行向量化，从而有效提高代码速度。