小白也能学会的深度学习3

2.1 二分类

在这个章节，我们会学习一些实现深度学习的重要技巧。例如有一个包含x个样本的训练集，你很可能习惯于用一个 for 循环来遍历训练集中的每个样本，但是当实现一个神经网络的时候，我们通常不直接使用 for 循环来遍历整个训练集。

首先我们先来看一下什么是二分类

二分类（Binary Classification）是机器学习中的一种基本任务，目标是从给定的输入数据中预测两个可能的结果之一。

假如你有一张图片作为输入，比如这只猫，如果识别这张图片为猫，则输出标签 1 作为结果；如果识别出不是猫，那么输出标签 0 作为结果。现在我们 可以用字母y来表示输出的结果标签，如下图所示：

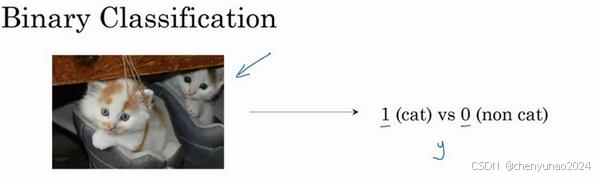
通常二分类代表的是一类问题，那么怎么解决二分类问题呢？

解决二分类问题的方法有很多，常见的包括但不限于：

逻辑回归（Logistic Regression）
支持向量机（Support Vector Machine, SVM）
决策树（Decision Tree）
随机森林（Random Forest）
神经网络（Neural Networks）

2.2今天我们首先来看一下逻辑回归

逻辑回归（Logistic Regression）也是一种分类算法，主要用于预测一个事件发生的概率。

 

符号比较难打，同时这个确实对于后续的理解很重要，所以我这里给你贴一下。

对于二元分类问题来讲，给定一个输入特征向量x，它可能对应一张图片，你想识别这 张图片识别看它是否是一只猫或者不是一只猫的图片，你想要一个算法能够输出预测，你只能称之为y^，也就是你y的估计。更正式地来说，你想让 y^ 表示y 等于 1 的一 只猫可能性或者是机会，前提条件是给定了输入特征x。换句话来说，如果x是我们在上个视频看到的图片，你想让y^ 来告诉你这是一只猫的图片的机率有多大。

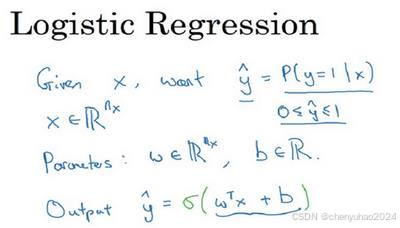
逻辑回归通过将线性回归的结果映射到一个0到1之间的值来实现分类。这个值是由Sigmoid函数（或Logistic函数）的非线性变换完成的。我们通常都使用z来表示wx+b的值。X是一个n下标x维的向量（相当于有x个特征的特征向量）。我们用w来表示逻辑回归的参数，这也是一个维向量（因为w实际上是特征权重，维度与特征向量相同），参数里面还有b,这是一个实数（表示偏差）。所以给出输入x以及参数w和b之后，我们怎样产生输出预测值)，一件你可以尝试却不可行的事是让夕=wx+b。

逻辑回归的输出是一个介于0和1之间的概率值，表示某个样本属于正类（通常标记为1）的概率。具体来说：

如果输出的概率大于0.5，则预测该样本属于正类。
如果输出的概率小于等于0.5，则预测该样本属于负类（通常标记为0）。

其中 z 是线性组合的结果，形式为：
z=β0​+β1​x1​+β2​x2​+⋯+βn​xn​  类似于加权平均数的概念。
这里，β0​,β1​,…,βn​ 是模型参数，x1​,x2​,…,xn​ 是输入特征。

也就是说，这里的x'维度向量越多，算出的β参数越多，对于z的估值就越精确。但是这里就会有一个问题，算力的消耗太大，损失太大，效率不高。那怎么优化呢？我们下一篇讲。感谢您的观看