高等数学（第六章：二重积分）

---

一、二重积分的对称性与比大小

1. 二重积分的概念

2. 二重积分的性质

3. 二重积分的对称性

1）奇偶对称

若 D 关于 x = a 对称，则 ∬_D (x-a) dxdy = 0 ；若 D 关于 y = b 对称，则 ∬_D (y-b) dxdy = 0 。

【例题】：设 D：x² + y² ≤ 2·x ，则 I = ∬_D (2·x+3·y) dxdy = ?

【解析】：D 为 (x-1)² + y² ≤ 1 ，可知 D 关于 x = 1 和 y = 0 对称，即 ∬_D (x-1) dxdy = ∬_D y dxdy = 0 ，有：I = ∬_D (2·x+3·y) dxdy = ∬_D 2·(x-1) dxdy + ∬_D 3·y dxdy + ∬_D 2 dxdy = ∬_D 2 dxdy = 2·π 。

学会分割区域 D 很重要！

例如：

• 设 D 是 xOy 平面上以 A(1,1) , B(-1,1) , C(-1,-1) 为顶点的三角形区域，D₁ 是 D 在第一象限的部分，则 I = ∬_D [x·y + cos(x)·sin(y)] dxdy = 2·∬_D1 [cos(x)·sin(y)] dxdy 。（用 y = -x 分割区域 D）

• 设平面 D = {(x,y) | x³ ≤ y ≤ 1 , -1 ≤ x ≤ 1} ，f(x) 是定义在 [-a,a]（a ≥ 1）上的任意连续函数，则 ∬_D [(x+1)·f(x) + (x-1)·f(-x)]·sin(y) dxdy = 0 。（用 y = -x³ , y ≥ 0 分割区域 D）

2）轮换对称

【总结】：

① 将区域 D 中的 x,y 与 f(x,y) 中的 x,y 同时对调，值不变。
即：∬_D(x,y) f(x,y) dσ = ∬_D(y,x) f(y,x) dσ 天然成立

② 若区域 D 关于 y = x 对称，将被积函数的 x 与 y 对调，值不变。
即：∬_D f(x,y) dσ = ∬_D f(y,x) dσ

• 进一步的，I = ∬_D f(x,y) dσ = ∬_D f(y,x) dσ = (1/2)·∬_D [f(x,y) + f(y,x)] dσ 。

• 更进一步的，
  若 f(x,y) = f(y,x) ，则 ∬_D f(x,y) dσ = 2·∬_D1 f(x,y) dσ
  若 f(x,y) = -f(y,x) ，则 ∬_D f(x,y) dσ = 0 。

4. 二重积分比大小

积分区域控制了被积函数的大小。

① 积分区域相同，比较被积函数的大小；

② 积分区域不同，比较被积函数的大小（不同积分区域的 x,y 取值不同）。

【方法】：

• 比 1 大，越平方越大，越根号越小；

• 比 1 小，比 0 大，越平方越小，越根号越大。

【例题】：设 I₁ = ∬_D cos√(x²+y²) dσ 、I₂ = ∬_D cos(x²+y²) dσ 、I₁ = ∬_D cos(x²+y²)² dσ ，其中 D = {(x,y) | x²+y² ≤ 1} ，则它们之间的大小关系为？
答案：I₃ > I₂ > I₁ 。

5. 二重积分定义

lim_n→∞ (1/n²)·∑_i=1ⁿ∑_j=1ⁿ f[(i/n),(j/n)] = ∫₀¹dx·∫₀¹ f(x,y) dy 。

6. 二重积分的换元

二、二重积分作图定限

1. 积分换系（直角坐标⇔极坐标）

极坐标与直角坐标互换很重要！因此需要掌握如何画出极坐标与直角坐标的积分区域。

• 极坐标表示：x = r·cosθ ；y = r·sinθ ；tanθ = y/x 。

• ∬_D f(x,y) dσ = ∫_α^βdθ · ∫_r1^r2 f(r·cosθ , r·sinθ) r·dr（需要确定 θ 角度和 r 上下限）。

• r = secθ（r·cosθ = 1）、r = cscθ（r·sinθ = 1）表示线；r = cosθ 、r = sinθ（两边同乘 r）表示圆；θ = π/4 表示直线 y = x。

• 当被积函数或积分区域出现了 x²+y² 或 x/y 这样的式子可以考虑利用极坐标。

极坐标角度定限问题：当积分区域手画不出来，没法从图形上来确定角度的上下限时，可以直接从积分区域边界曲线的表达式来确定上下限。

2. 积分换序

1）直角坐标

① x 型区域：

② y 型区域：

③ 直角坐标系的换序问题：

2）极坐标

① θ 型区域：

② r 型区域：

③ 极坐标下的换序问题：

二重积分换序的应用：

• 定积分（或反常积分）转换成二重积分，然后换序计算。

• 对被积函数逆用牛顿莱布尼茨公式产生一重积分，从而原定积分（或反常积分）转换成二重积分，然后换序计算。

• 对等式或不等式中的变量积分，产生二重积分，然后换序计算。

三、二重积分计算总结

1. 求直极综合二重积分

【做题步骤】：

• 第一步：画出积分区域 D ；

• 第二步：根据积分区域 D 和被积函数，看是否能根据偶倍奇零进行初步化简；

• 第三步：选择积分方法。

1）利用对称性（奇偶对称+轮换对称）

• 奇偶对称：若 D 关于 x = a 对称，则 ∬_D (x-a) dxdy = 0 ；若 D 关于 y = b 对称，则 ∬_D (y-b) dxdy = 0 。

• 轮换对称：将区域 D 中的 x,y 与 f(x,y) 中的 x,y 同时对调，值不变；若区域 D 关于 y = x 对称，将被积函数的 x 与 y 对调，值不变。

2）利用广义极坐标

关于 dxdy 的变换：dxdy → |∂(x,y)/∂(u,v)|dudv 。

• 偏心圆 dxdy → r·drdθ（平移变换 + 极坐标变换）；

• 椭圆 dxdy → abr·drdθ（伸缩变换 + 极坐标变换）。

下面举几个例子：

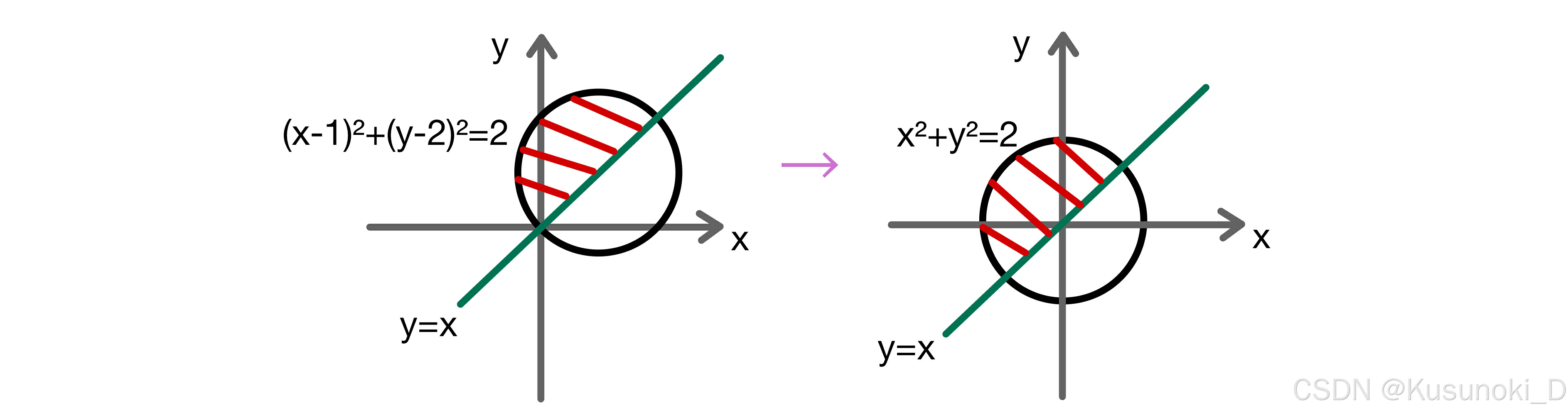
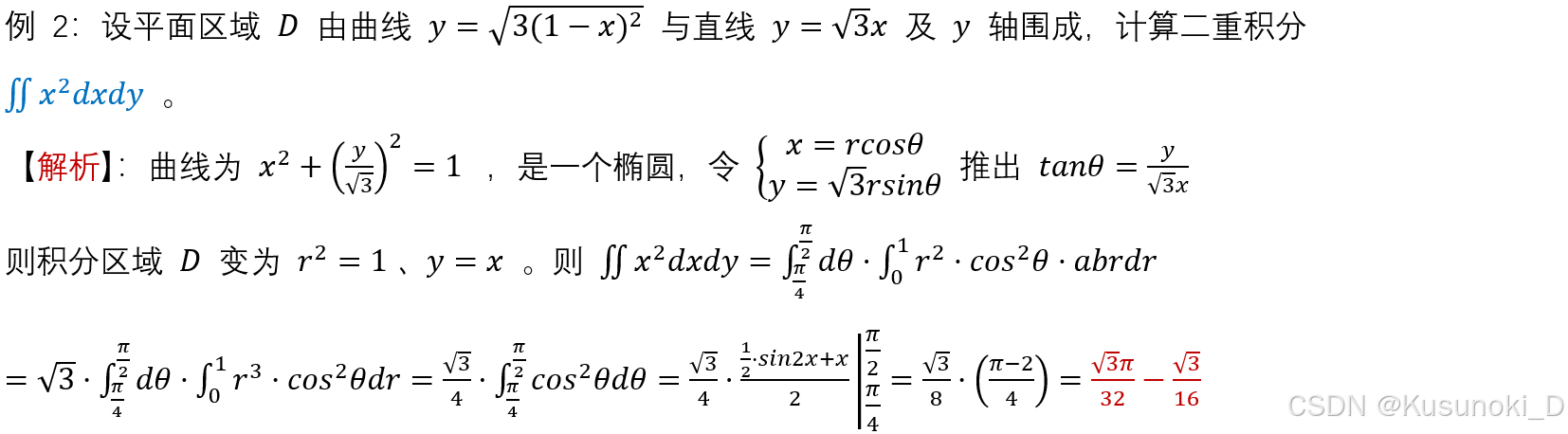
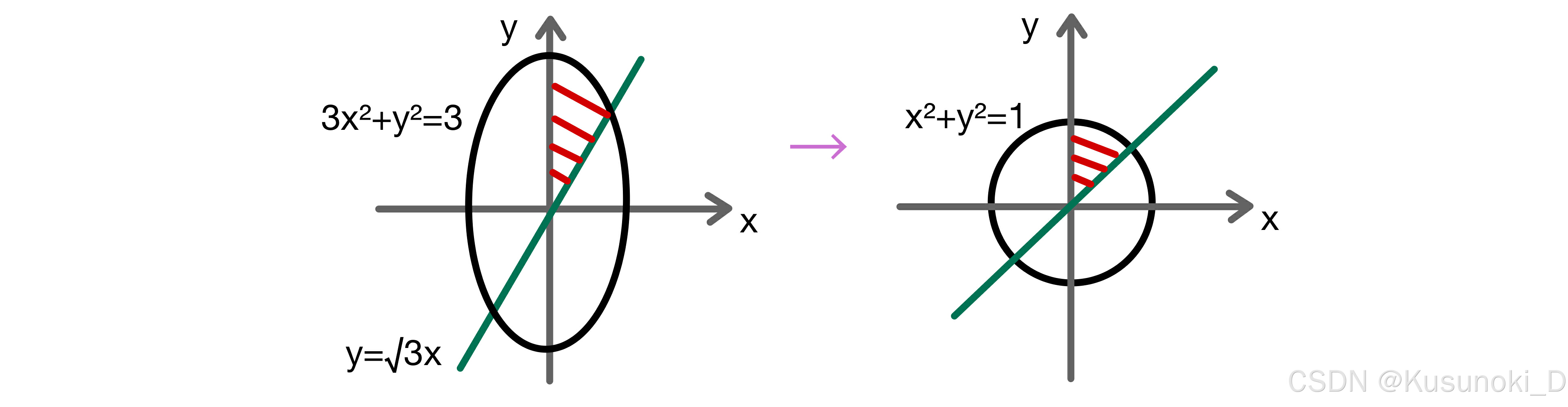
3）利用极坐标换序

把 θ 视为横坐标变量 x ，把 r 视为纵坐标变量 y ，把极坐标下的换序问题转变成直角坐标系的换序问题。

2. 求绝对值函数二重积分

设 D₂ = D - D₁ ，则有 ∬_D₂ - ∬_D₁ = ∬_D - ∬_D₁ - ∬_D₁ = ∬_D - 2·∬_D₁ 。

3. 求最值函数二重积分

例题：

• 计算 ∬_D max{xy,1} dxdy ，其中 D = {(x,y)|0≤x≤2,0≤y≤2} 。【答案：19/4 + ln2】
  ① D₁：0≤x≤2,0≤y≤2 且 y≥(1/x) ；
  ② D₂：0≤x≤2,0≤y≤2 且 y<(1/x) ；
  ∬_D max{xy,1} dxdy = ∬_D₁ xy dxdy + ∬_D 1 dxdy 。

• 计算 I = ∬_D max{x,y}·|y-x²| dxdy ，其中 D = {(x,y)|0≤x≤1,0≤y≤1} 。【答案：11/40】
  ① D₁：0≤x≤1,0≤y≤1 且 y≥x ；
  ② D₂：0≤x≤1,0≤y≤1 且 x²≤y<x ；
  ③ D₃：0≤x≤1,0≤y≤1 且 y<x² ；
  ∬_D max{x,y}·|y-x²| dxdy = ∬_D₁ y·(y-x²) dxdy + ∬_D₂ x·(y-x²) dxdy + ∬_D₃ x·(x²-y) dxdy 。

4. 求分段函数二重积分

5. 求取整函数二重积分

【例题】：设 D：0≤x≤2,0≤y≤2 ，计算 ∬_D [1+x+y] dxdy ，其中 [1+x+y] 表示不超过 1+x+y 的最大整数。

【解析】：在 0≤x≤2,0≤y≤2 的范围内，有 0≤x+y≤4 ，若：

• 令区域 D₁ 为 -x ≤ y < 1-x ，则 [1+x+y] = 1 ；

• 令区域 D₂ 为 1-x ≤ y < 2-x ，则 [1+x+y] = 2 ；

• 令区域 D₃ 为 2-x ≤ y < 3-x ，则 [1+x+y] = 3 ；

• 令区域 D₄ 为 3-x ≤ y < 4-x ，则 [1+x+y] = 4 。

则有：∬_D [1+x+y] dxdy = ∬_D₁ 1 dxdy + ∬_D₂ 2 dxdy + ∬_D₃ 3 dxdy + ∬_D₄ 4 dxdy = (1/2) + 2·(3/2) + 3·(3/2) + 4·(1/2) = 10 。

6. 求符号函数二重积分

符号函数 sgn(x)：x < 0 时 sgn(x) = -1 ；x = 0 时 sgn(x) = 0 ；x > 0 时 sgn(x) = 1 。

7. 求参数方程二重积分

【思路】：先在直角坐标下化成累次积分。

【拓展】：

逆用格林公式求二重积分

四、二重积分综合题

1. 二重积分求极限

1）二重积分中值定理

设函数 f(x,y) 在有界闭区域 D 上连续，则在 D 上至少存在一点 (ξ,η) ，使得 ∬_D f(x,y) dσ = f(ξ,η)·∬_D 1 dσ = f(ξ,η)·S_D 。

注：椭圆 x²/a² + y²/b² = 1 的面积为 πab 。

2）洛必达求导（0/0 型或 ∞/∞ 型）

举几个求导的例子：

• φ(t) = ∫₁^t du · ∫₀^u² arctan(1+x) dx ，则 φ’(t) = ？
  把 ∫₀^u² arctan(1+x) dx 看成 g(u) ，有 φ’(t) = g(t) = ∫₀^t² arctan(1+x) dx

• φ(t) = ∫₁^t dy · ∫_y^t f(x) dx ，则 φ’(t) = ？
  先换序，再求导：φ(t) = ∫₁^t dx · ∫₁^x f(x) dy ⇒ φ’(t) = (t-1)·f(t) 。

• φ(t) = ∫₀^t dx · ∫_t^x e^-y² dy ，则 φ’(t) = ？
  先换序，再求导：φ(t) = -∫₀^t dy · ∫₀^y e^-y² dx ⇒ φ’(t) = -t·e^-t² 。

3）交换积分次序

∫dx·∫dy ⇔ ∫dy·∫dx ；∫dθ·∫dr ⇔ ∫dr·∫dθ 。必要时对积分进行换元。

2. 二重积分是一个数

模型题：设 f(x,y) = g(x,y) + ∬_D f(u,v) dudv ，求 f(x,y) 的表达式。

【思路】：

• 令 A = ∬_D f(u,v) dudv（A 是一个数），有 f(x,y) = g(x,y) + A ；

• （两边同时积分）则 ∬_D f(x,y) dxdy = ∬_D g(x,y) dxdy + A·∬_D 1 dxdy = A ；

• 由此，只要解出 ∬_D g(x,y) dxdy 和 ∬_D 1 dxdy 就可以得到 A 的值，从而由 f(x,y) = g(x,y) + A 得到 f(x,y) 的表达式。

3. 利用分部积分法

模型题：设 f(x) = ∫_c^x g(t) dt ，求 I = ∫_a^b x·f(x) dx 。

【思路】：

• （分部积分法）I = ∫_a^b x·f(x) dx = (1/2)·∫_a^b f(x) dx² = (1/2)·[x²·f(x)|_a^b - ∫_a^b x²·f’(x) dx] ；

• （化简）得到 I = (1/2)·{[b²·f(b) - a²·f(a)] - ∫_a^b x²·g(x) dx} ，从而将二重积分转换成了一重积分，只需要计算出 ∫_a^b x²·g(x) dx 的值即可。

该类型的题目还可以使用二重积分换序的方法：∫ dx · ∫ dt ⇒ ∫ dt · ∫ dx 。

4. 雅可比换元法

雅可比换元：∬_D f(x,y) dxdy = ∬_D f(u,v)·|J| dudv 。

下面给出一道利用雅可比进行换元的例题：

5. 二重积分证明题

重要不等式：|∬_D f(x,y) dxdy| ≤ ∬_D |f(x,y)| dxdy 。一些常用的不等式需要熟记！

6. 二重积分结合题