一. 选择

1. 利用二重积分不等式性质
- B
利用二重积分不等式性质:函数大小+父函数递减
2. 二重积分定义的形式(1. 积分形式,2.被积函数)
交换积分次序(极坐标到直角坐标)
- 对:
先由极坐标:θ和r的取值范围,可直接化为直角坐标的上下限的表达式。
画图,定先后积分次序。
二. 填空题

1. 根据被积函数(看成一元)找到正负的边界
- 通过被积函数的的正负来划分不同的积分区域
2. 画对积分区域的步骤
- 把握复合函数的范围
- 画图像时别跳步
2. 交换积分次序
2.1. 当前积分不好积分时
对
2.2. 极坐标系看成直角坐标系进行积分
- 变换积分次序
注意这不是极坐标系,是直角坐标系,进而简化积分。
- 变换坐标
5.1. 技巧是:可以将极坐标将θ看成x,r看成y
5.2. 注意求反函数时,θ的值(由sinx的图像可知)
0到π的arcsinx图像
广义极坐标ing(不要求)
- 广义极坐标(ing)
极坐标下的二重积分(面积与体积)
积分区域可由曲线满足的意义来决定
- 求面积
- 由r可得出θ的符合范围
- 极坐标变换公式:θ和r的变化区间。
由定义:限定(截取)为积分区域、被截的为被积函数
- 求截面体积
圆柱面是限定区域,
因为是关于x、y的积分,所以分离出z。
限定部分有上下两部分,由对称性分成4份。
极坐标:为圆柱面。
形心求导公式
- 形心坐标公式
面积
- 形心
心型线公式:
三. 解答题

1. 不同区域下的积分
- 不同x看成整体积分
2. 关于y=x对称与不好积分变换极坐标
- 抓住积分特点:
2.1. 关于y=x对称,xy的互换性
2.2. 不好积分:变为极坐标积分
tanx积分公式
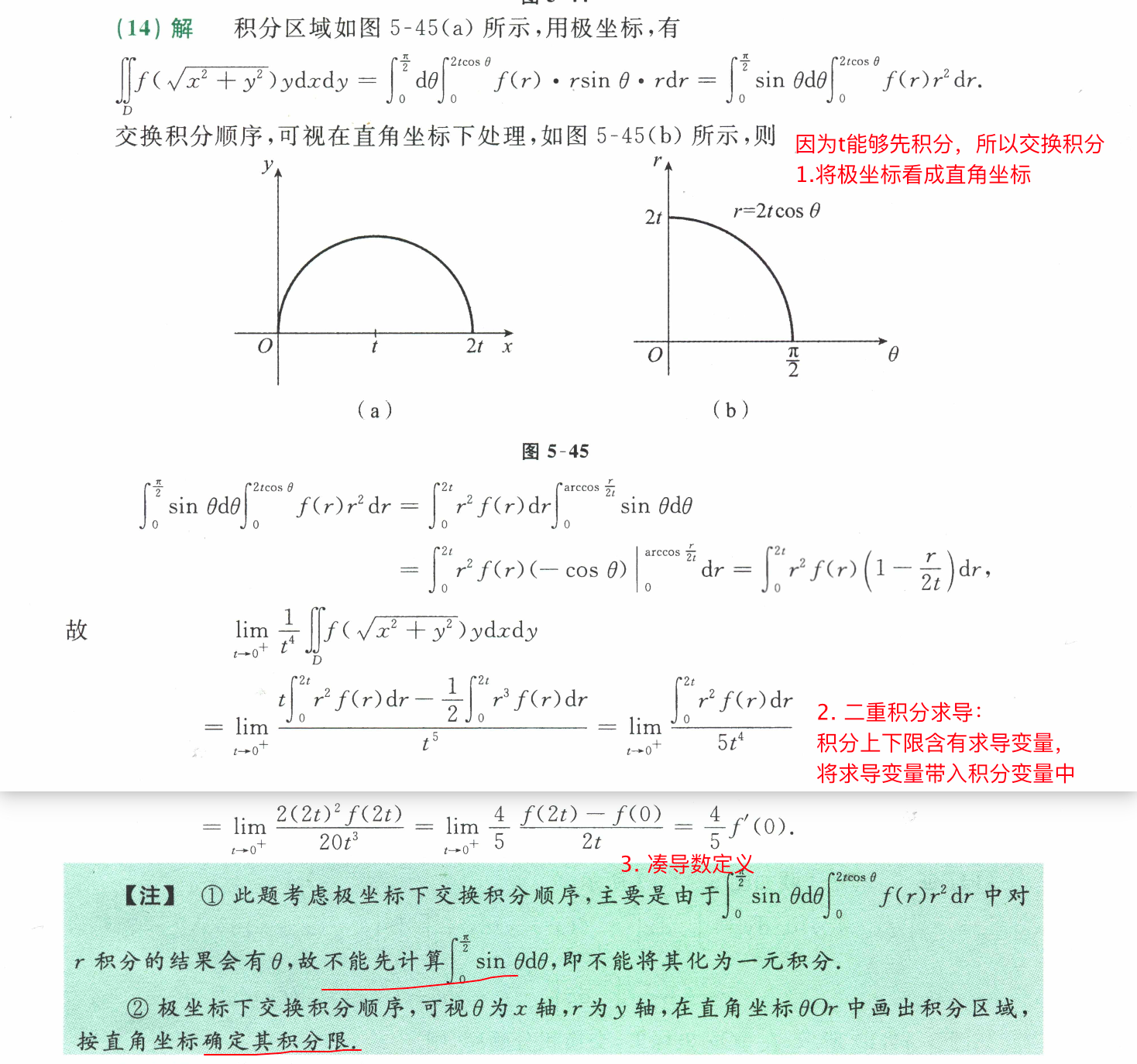
3. 二重积分求导:求导变量替换到第二个积分限中
- 对二重积分求导
- 交换积分次序
1.1 规整1:求导时,x不能在积分上下限中出现
1.2. 规整2对t求导,首次积分上下限中不能有t,- 求导时:
2.1. 首次积分y替换为t
2.2. 求导时被积函数不能有t,需进行变换
- 利用一元积分求导公式
补充题:
被积函数不能含有变上限参数,所以要交换积分次序
分清楚积分变量与求导变量
- 对于积分可以将其他变量的式子提出来
- 对于(对y)求导:积分限中要含有对应变量(y)
交换积分次序
- 对
注意对边界点的验证
二重积分求导、微分方程
- 对
5.1. 化成极坐标系
5.2. 容易看到θ和r比较容易分离,然后分别积分,再洛必达。下图方法比较复杂
6. 二重积分与微分方程

- 二重积分与一阶线性微分方程
将x看成常数、积分中值定理+多元微分定义
8.1. 将x看成常数
8.2. 交换积分次序:求导参数(x)放到一侧积分,用于简化求导
8.3. 利用积分中值定理:x看成常数
8.4. 微分展开+积分中值定理的定义
- (对) 设二重积分是一个数
几何应用:质心、形心
- 质心公式
极坐标变直角坐标
二重积分求导的公式
凑求导定义
四. 拓展题
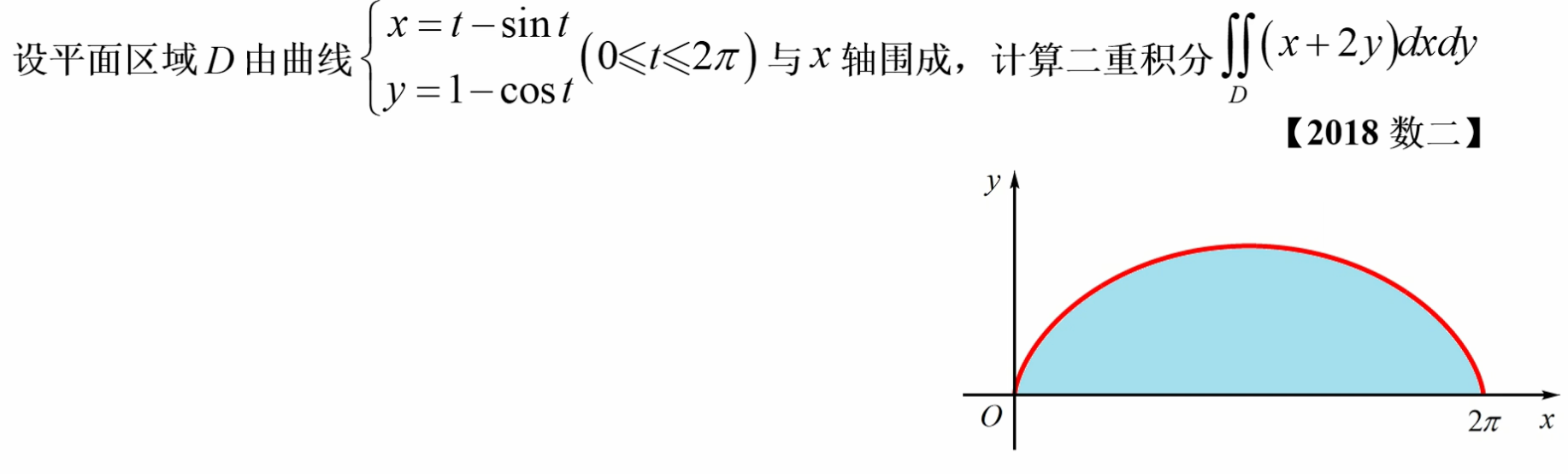
直接带入y(x)
三角函数积分公式






























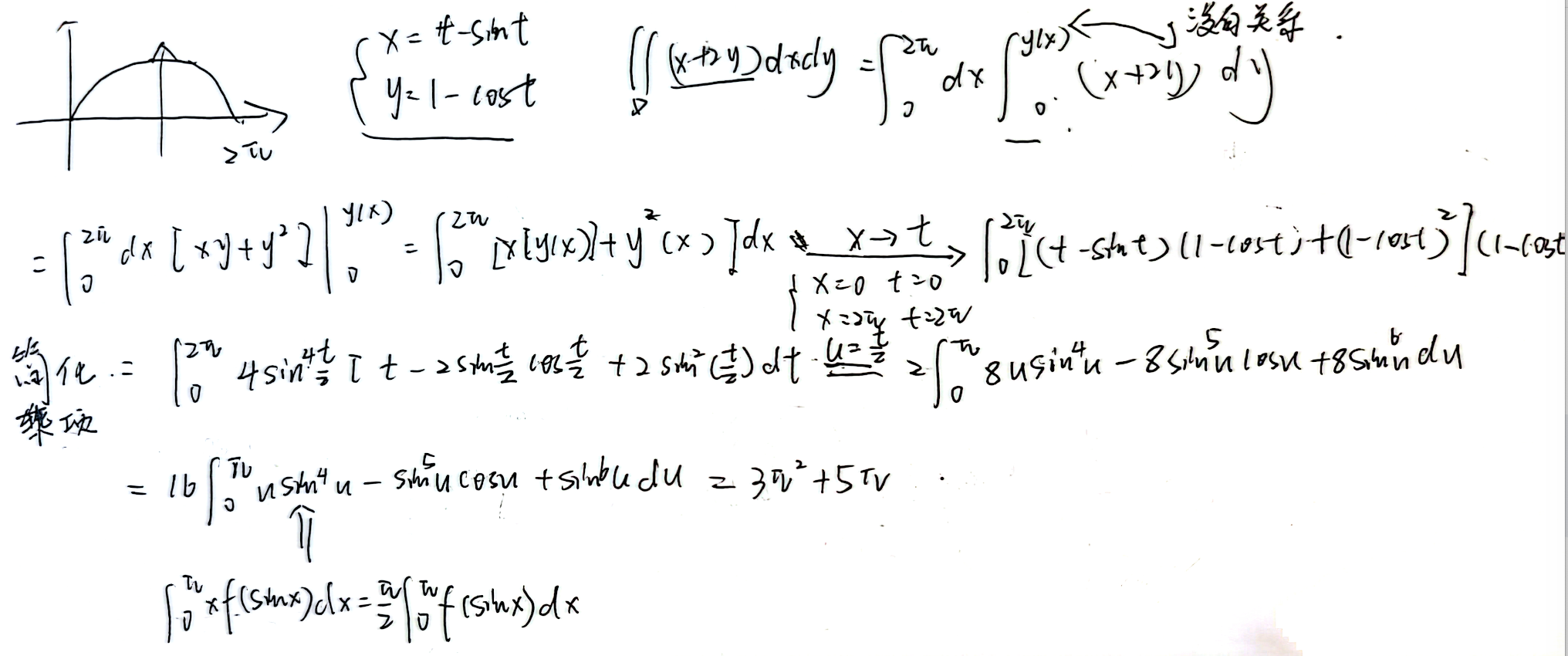
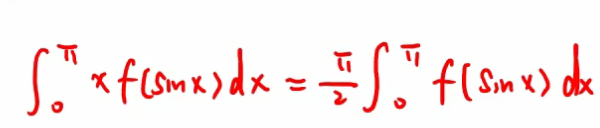

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










