练习一:用栈实现队列:. - 力扣(LeetCode)
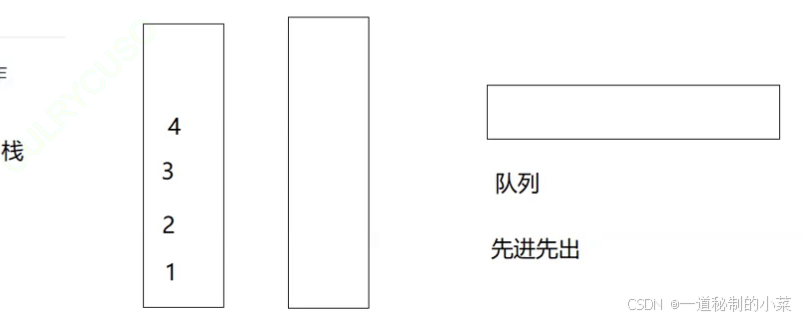
假设当前有4个数据插入栈中(插入顺序为1,2,3,4),此时如果想按照队列出数据,我们应该把1pop!
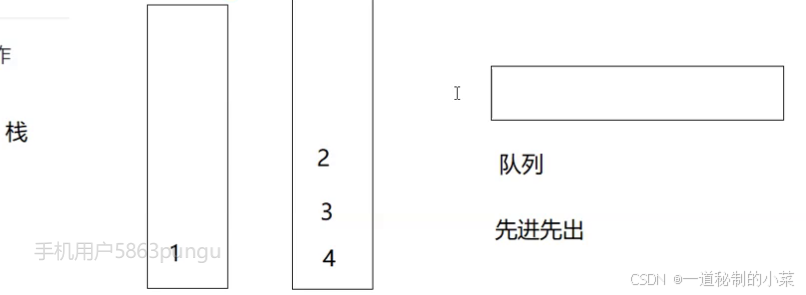
我们将数据导入另一个空栈,然后再将1pop!
此时发现第二个栈的顺序是对的,不需要再重新导入第一个栈中!(栈的数据倒一圈就翻过拉了!)
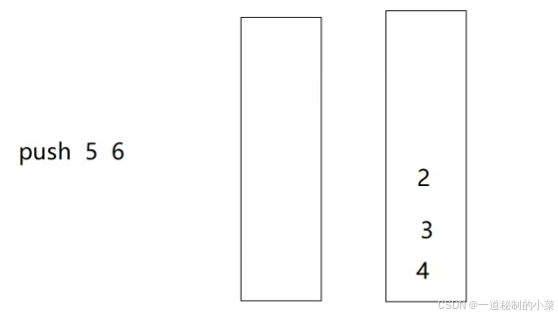
此时如果有数据需要push,不需要倒数据,直接将其插入到第一个栈中即可!
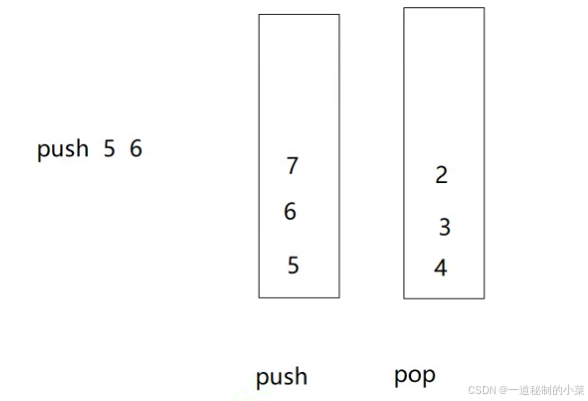
- 左边的栈一直入数据;
- 右边的栈一直出数据;
- 右边的栈的数据是左边的栈倒过来的!(右边的数据出空了就可以再从左边的导入!)
练习二:循环队列
拓展知识点:如何用数组实现链表?

整个数组是用一个大的结构体数组,其中每个元素都是一个小数组,元素中分别对应值和下一个元素的下标。(实际使用没有太大优势)
对于循环队列来说,我们可以使用数组来实现,也可以使用链表来实现;
大部分的同学可能认为链表来实现比较方便,但是其实链表实现的时候会出现很多大坑;
使用链表来实现循环队列:
1. 空链表的情况
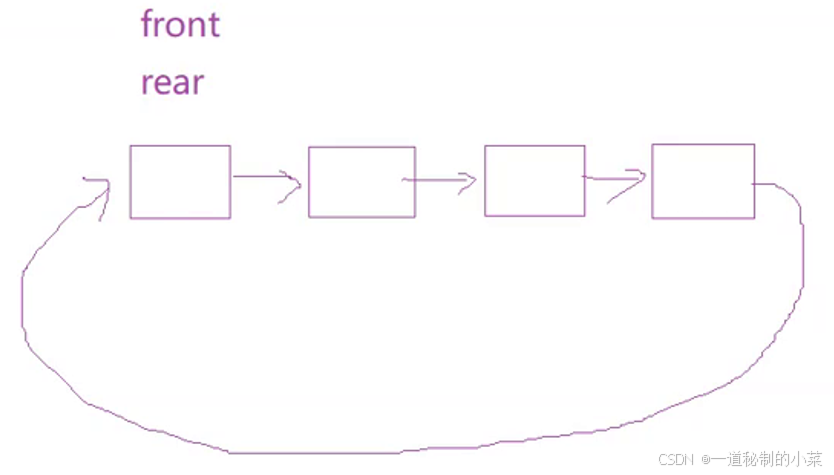
对于空的循环队列有上面这种情况:front - 队列的头 ; rear - 队列的尾
且最开始链表的头和尾指在同一位置;
2. 插入一个数据
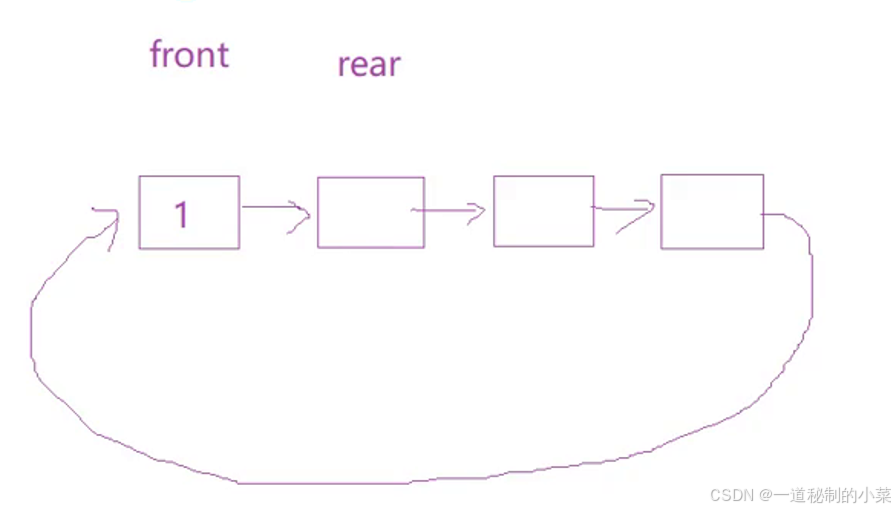
插入数据时,此时头不变,尾指向插入元素的下一个位置;
pop的时候相反:尾rear不变,头head向后移!
3. 当队列元素满时
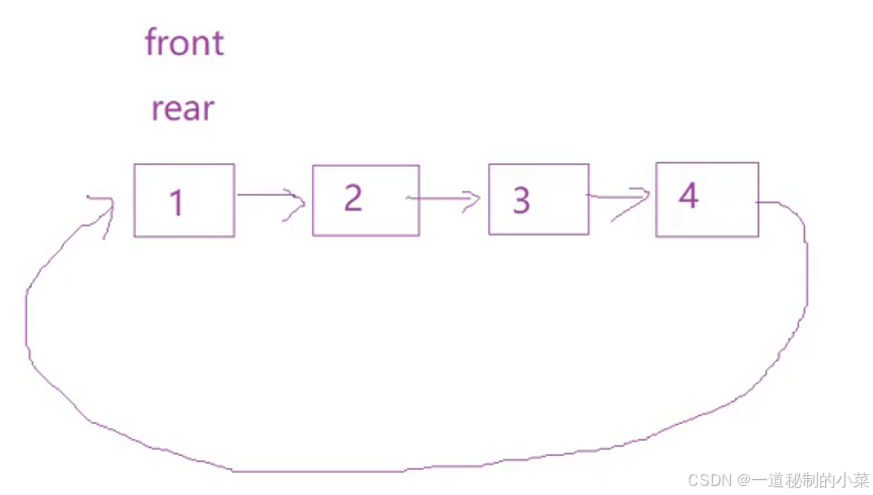
此时头和尾都指向同一个位置;
此时就会出现比较尴尬的情况:
头和尾都指向同一个位置的时候不能分辨是空队列还是满队列;
解决方法一:增加一个size
size不为空的时候说明队列满了;为空说明时空队列;
解决方案二:增加一个位置(不存数据)
空队列:
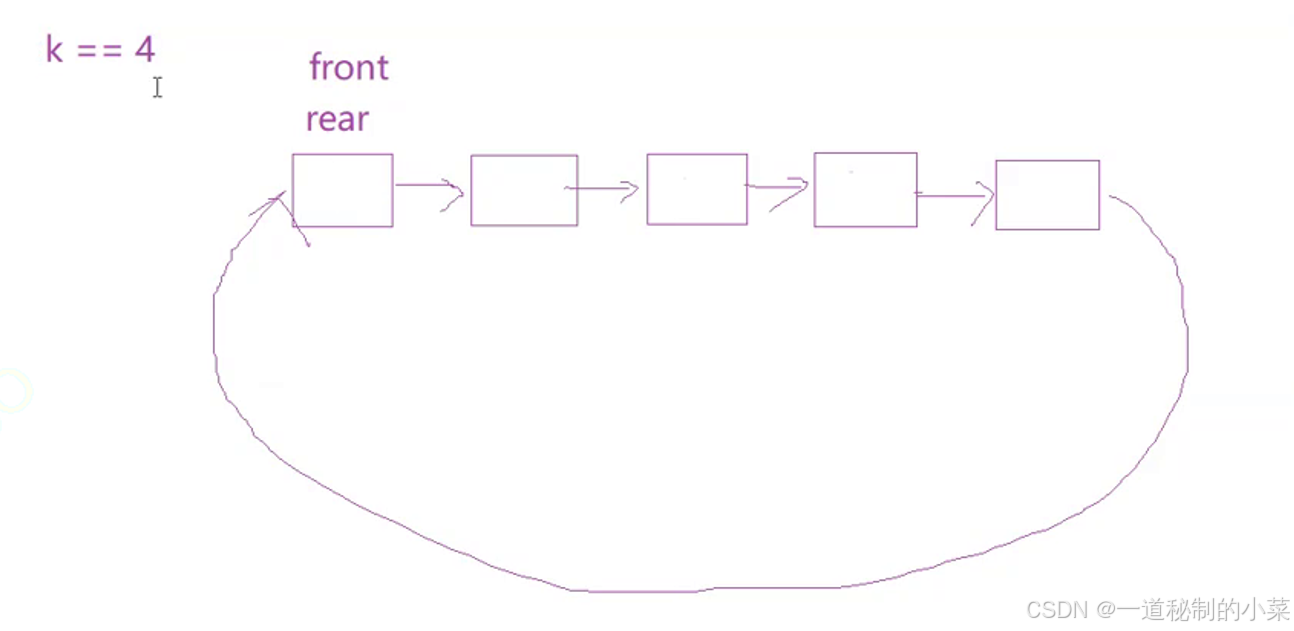
满队列:
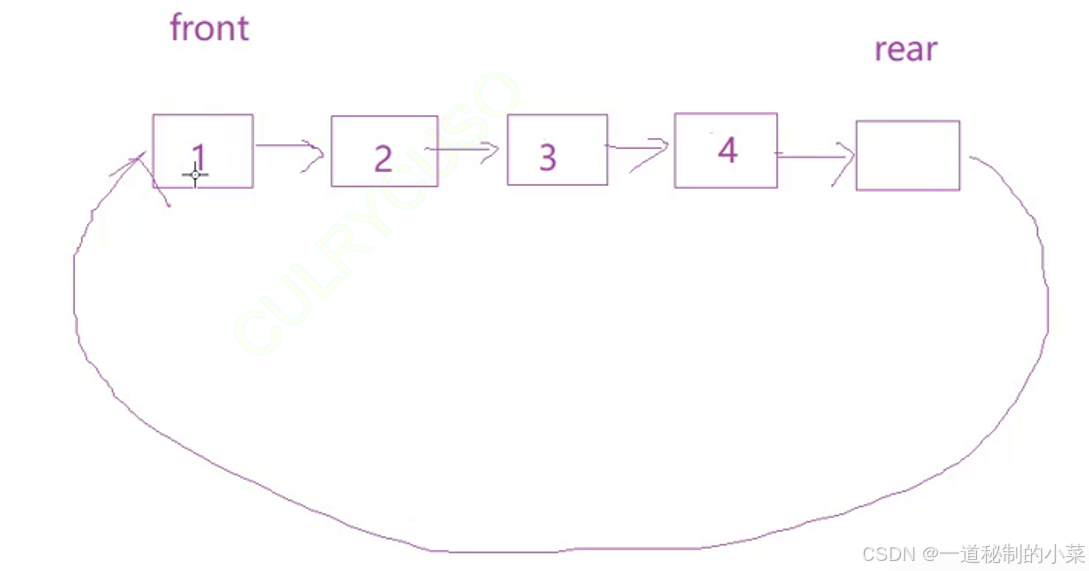
此时空队列的情况为head和rear在同一位置;
满队列的情况为rear的下一个位置是head;
但是对于这两种解决方法,使用单链表实现还有一个很大的弊端:找尾rear / 尾元素非常麻烦!
使用数组来实现循环队列:
我们可以跟上面的链表一样,每次多开一个空间,这个空间不存元素;
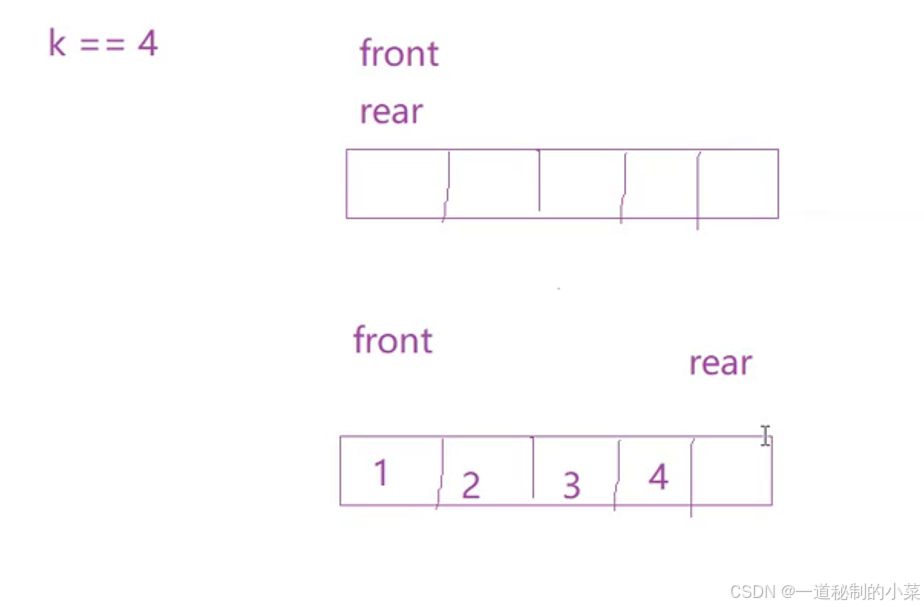
需要注意的是:如果下标在k+1的位置,需要进行 模 一下再继续进行;
接下来我们尝试使用数组来实现:
演示代码如下所示:
typedef struct {
int *a;
int front;
int rear;
int k;
} MyCircularQueue;
// 初始化队列
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue* obj = (MyCircularQueue*) malloc(sizeof(MyCircularQueue));
obj->a = (int*)malloc(sizeof(int) * (k+1));
obj-> front = 0;
obj-> rear = 0;
obj->k = k;
return obj;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->front == obj->rear;
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return (obj->rear+1) % (obj->k + 1) == obj->front;
}
// 插入元素
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if (myCircularQueueIsFull(obj))
return false;
obj->a[obj->rear] = value;
obj->rear++;
obj->rear %= (obj->k + 1);
return true;
}
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if (myCircularQueueIsEmpty(obj))
return false;
obj->front++;
obj->front %= (obj->k + 1);
return true;
}
int myCircularQueueFront(MyCircularQueue* obj) {
if (myCircularQueueIsEmpty(obj))
return -1;
else
return obj->a[obj->front];
}
int myCircularQueueRear(MyCircularQueue* obj) {
if (myCircularQueueIsEmpty(obj))
return -1;
return obj->a[(obj->rear-1 + obj->k+1) % (obj->k+1)];
}
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->a);
free(obj);
}树的存储方式:
如何定义一个树的结构?
左孩子右兄弟法则:

树分为结构里面有两个节点,分别只存第一个孩子和兄弟节点;
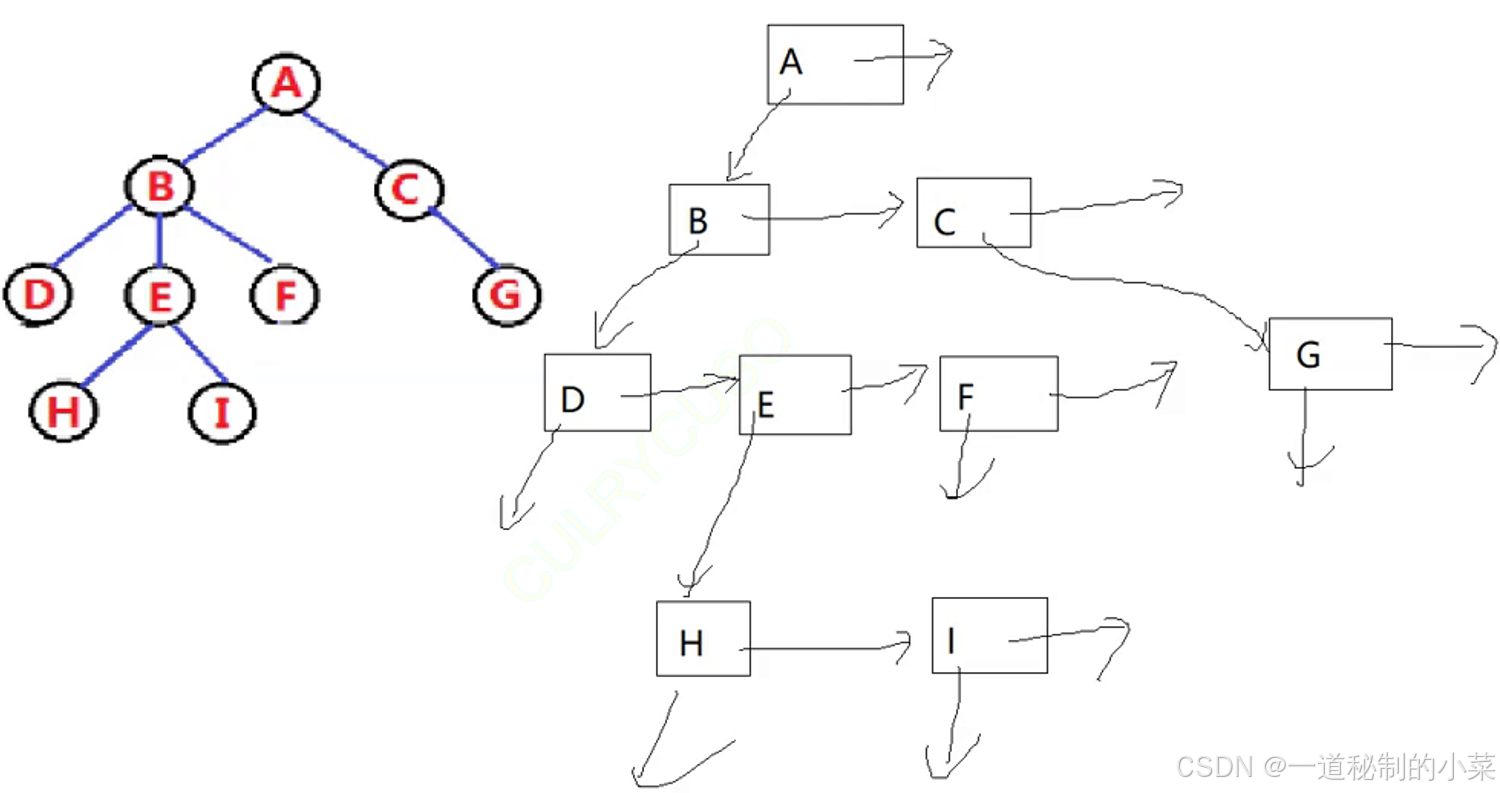 树的实际应用:
树的实际应用:
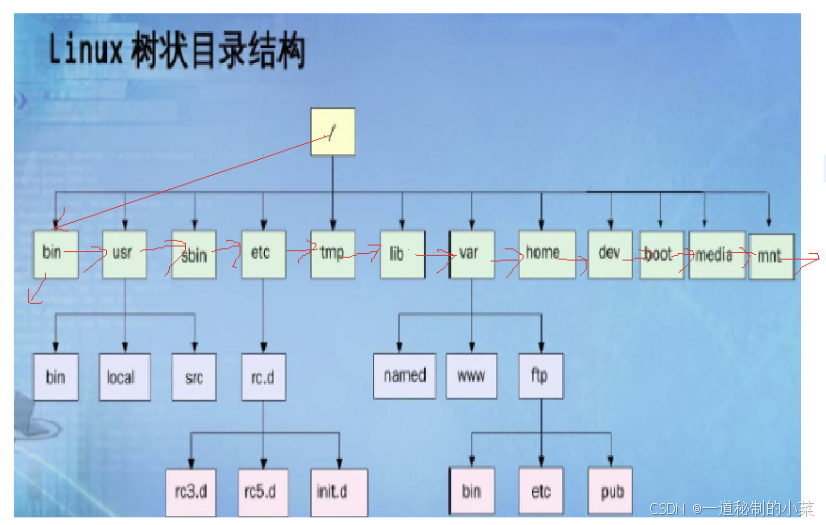
这里我们点击目录,实际上就是先展示第一个孩子节点,然后孩子节点依次展示兄弟节点;
新建目录实际上是在兄弟节点后面进行push;
二叉树
1. 概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空(空树);
- 由一个根节点加上两可别称为左子树和右子树的二叉树组成;
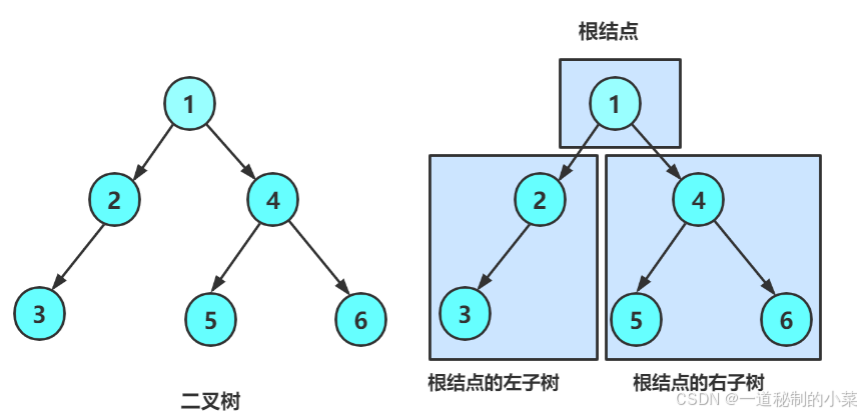
二叉树的一些特点:
- 二叉树不存在度大于2的结点;
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树有序的树;
2. 满二叉树和完全二叉树
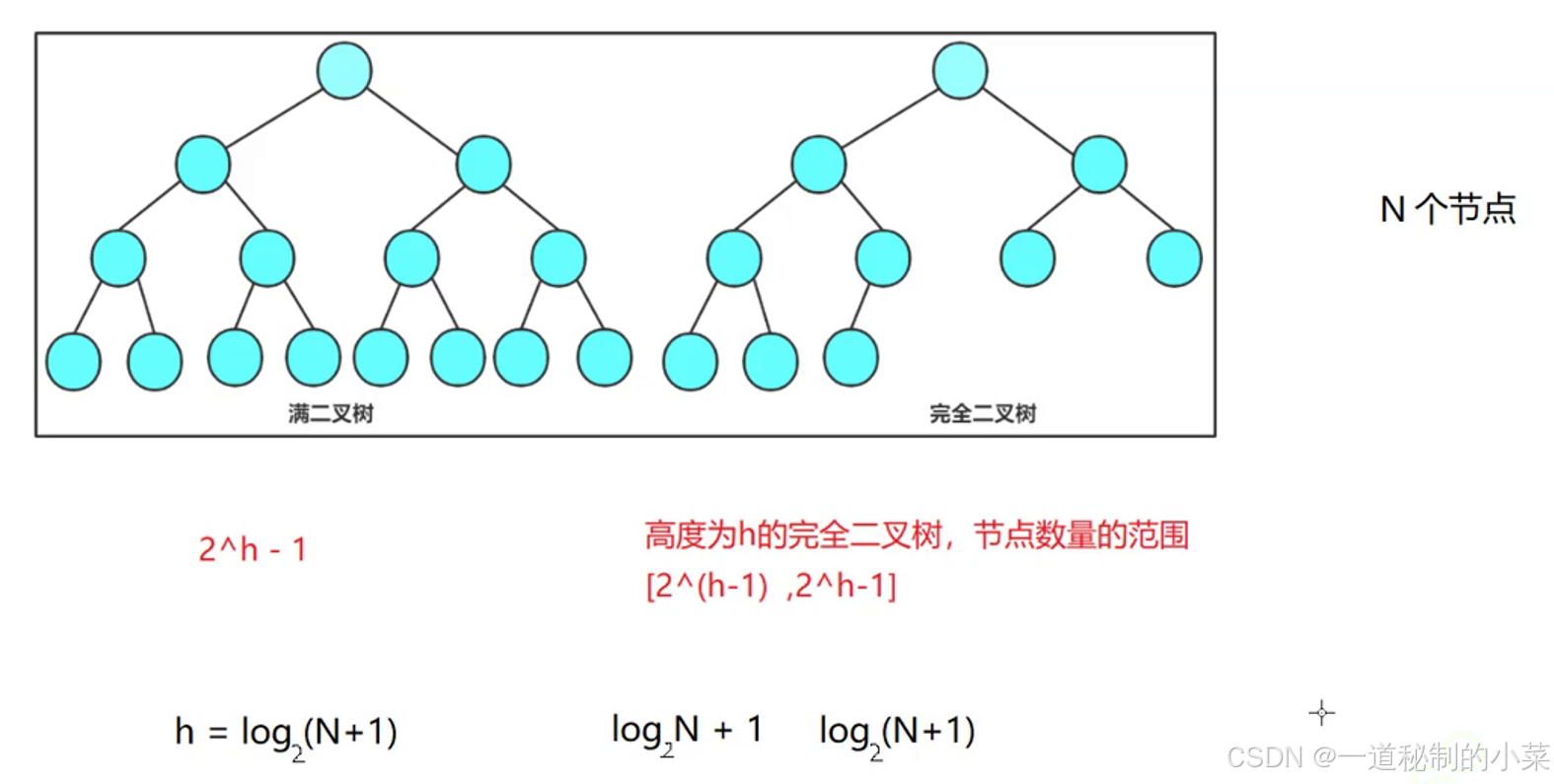
满二叉树:一个二叉树,如果每一层的结点数都达到最大值,则这个二叉树就是满二叉树;如果一个二叉树层数为K,且结点总数为2^k-1;
完全二叉树:假如我们的树有K层结构,满足前K-1曾都是满二叉树,最后一层要求从左到右是连续的,满足上面两个条件即为完全二叉树;完全二叉树的效率非常高!
满二叉树是特殊的完全二叉树!
结论:
- 1. 高度为H的完全二叉树,节点的数量范围为[2^(h-1) , 2^(h)-1];
- 二叉树性质:对任何一颗二叉树T,如果叶子数(度为0的结点个数)为n0, 度为2的结点数为n2,则n0 = n2+1;
- 完全二叉树的N1(度为1的结点个数)的结点个数要不为1,要不为0;

解题思路:



问题:如果已知结点的个数为N,那么满二叉树的高度和完全二叉树的高度分别为多少?
3. 二叉树的存储结构
二叉树一般可以使用两种结构进行存储:顺序结构和链式结构
1. 顺序结构
- 顺序结构存储是使用数组来进行存储,一般来说数组存储只适合表示完全二叉树,因为不是完全二叉树的话会存在空间上的浪费;
- 一般来说现实使用中只有堆才会使用数组来进行存储;
- 二叉树的顺序存储在物理上是一个数组,在逻辑上是一颗二叉树;
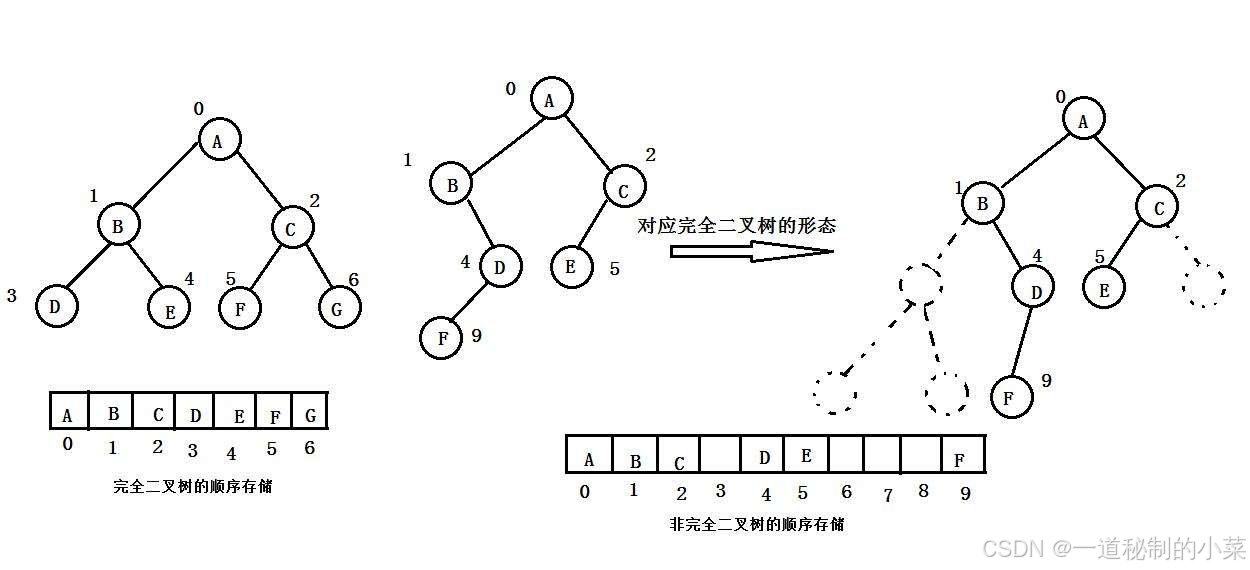
- 上图中二叉树形式是二叉树的逻辑结构;
- 下面的数组形式是物理结构;
- 可以看出非完全二叉树存在空间上的浪费;
对于二叉树来说,二叉树的值在数组中的父子下标的关系为:
- parent = (child - 1) / 2;
- leftchild = 2 * praent + 1;
- rightchild = 2* parent + 2;
关于链式存储我们后面讲二叉树的存储方式的时候再详细讲解;





















 801
801

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










