基于Python3的数据结构与算法 - 05 堆排序

目录

一、堆排序之树的基础知识

1. 树的定义

2. 树的一些概念

二、堆排序二叉树的基本知识

1. 二叉树的定义

2. 二叉树的存储方式（表达方式）

2.1 顺序存储方式

三、堆

1. 堆的定义

2. 堆的向下调整性质 

四、堆排序的过程 

1. 建造堆

五、时间复杂度

六、内置模块

---

一、堆排序之树的基础知识

1. 树的定义

1. 树是一种数据结构  比如：目录结构
2. 数是一种可以递归定义的数据结构
3. 树是由n个节点组成的集合：

• 如果n = 0，那这是一棵空树；
• 如果n > 0，那存在1个节点作为树的根节点，其他节点可以分为m个集合，每个集合本身优势一棵树。

2. 树的一些概念

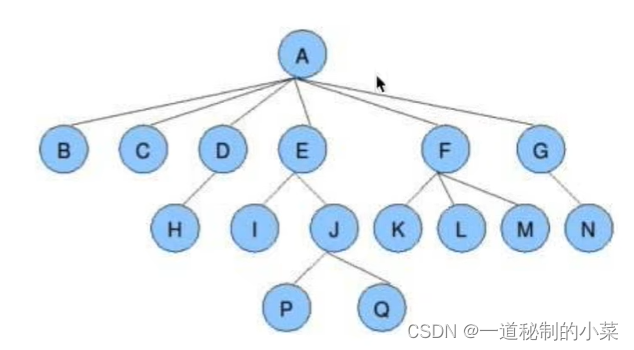
1. 根节点、叶子节点：根节点如下图的A；叶子节点：不能分叉的节点为叶子节点（BCHIKLMNPQ）
2. 树的深度(即结构共有几层，如下图树的结构有4层，A为第1层，P,Q为第4层)
3. 树的度（即在树中，那个节点的分叉数最多，如下图中的A，树的度为6）
4. 孩子节点/父节点（如E节点中，E是I的父节点；I是E的子节点）
5. 子树（整个树中的一部分，例如EIJQO即为子树。）

二、堆排序二叉树的基本知识

1. 二叉树的定义

二叉树：度不超过2的树，即每个节点最多有两个孩子节点，且两个孩子节点被区分为左孩子节点和右孩子节点。

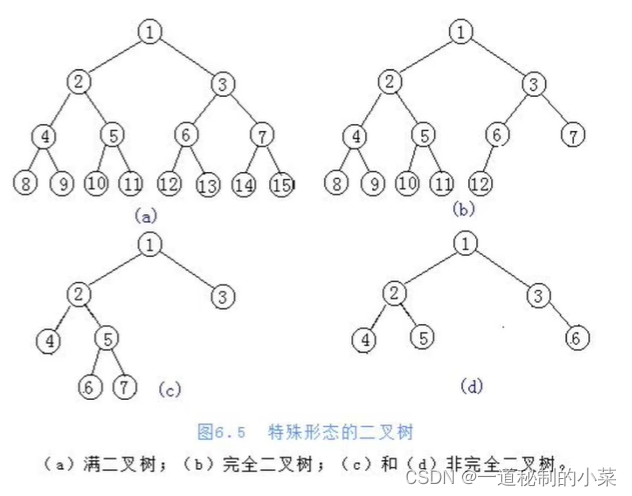
满二叉树：一个二叉树，如果每一层的结点数都达到最大值，则这个二叉树就是满二叉树。

完全二叉树：叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。（从满二叉树最后一层拿走几个节点；即相对于满二叉树，最下面一层可以不满，但必须从左到右依次排过来）

2. 二叉树的存储方式（表达方式）

• 链式存储方式
• 顺序存储方式（堆排序，用列表来存）

2.1 顺序存储方式

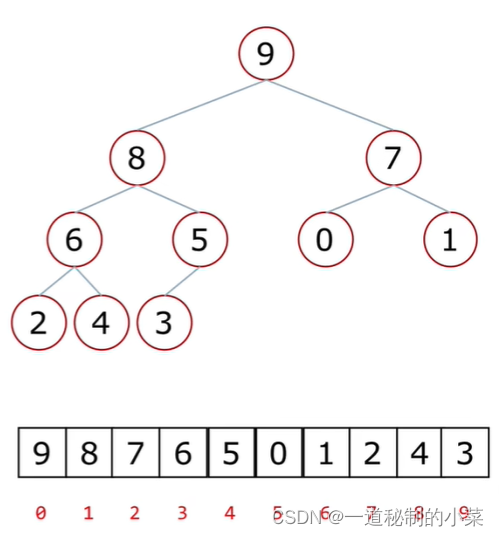
观察上图父节点 和孩子节点的编号下标的关系

1. 父节点与左孩子节点的编号下标的关系：

•  0-1  1-3  2-5  3-7  4-9
•  i → 2i+1

2. 父节点与右孩子节点的编号下标的关系：