1.连续函数的卷积

1.1 将图1中的两个函数的表达式写出
x(t)={1, 0<t<3T0,其他
x(t)=
\begin{cases}
1, & \ 0<t<3T\\
0, &其他
\end{cases}
x(t)={1,0, 0<t<3T其他
h(t)={t2T,0<t<2T0,其他
h(t)=
\begin{cases}
\cfrac t{2T} , &0<t<2T\\
0, &其他
\end{cases}
h(t)=⎩⎨⎧2Tt,0,0<t<2T其他
1.2 分类讨论
情况1情况1情况1
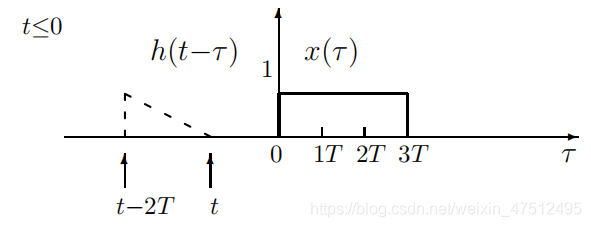
显然y(t)=0。显然 y(t)=0。显然y(t)=0。
情况2情况2情况2
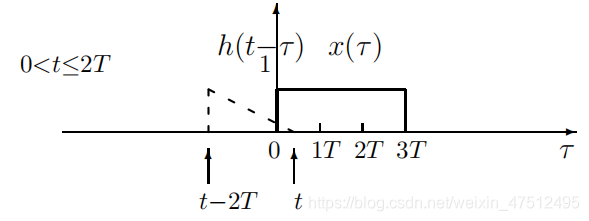
y(t)=∫0tx(τ)h(t−τ)dτ=12T∫0t(t−τ)dτ=t24Ty(t)=\int_0^tx(\tau)h(t-\tau)d{\tau}=\cfrac1{2T}\int_0^t(t-\tau)d\tau=\cfrac {t^2}{4T}y(t)=∫0tx(τ)h(t−τ)dτ=2T1∫0t(t−τ)dτ=4Tt2
注意看两个函数重叠部分,此时t<0时卷积结果为0,所以积分下限为0,积分上限为不断移动的函数h(t−τ)注意看两个函数重叠部分,{此时t<0时}卷积结果为0,所以积分下限为0,积分上限为不断移动的函{数h(t-\tau)}注意看两个函数重叠部分,此时t<0时卷积结果为0,所以积分下限为0,积分上限为不断移动的函数h(t−τ)
情况3情况3情况3
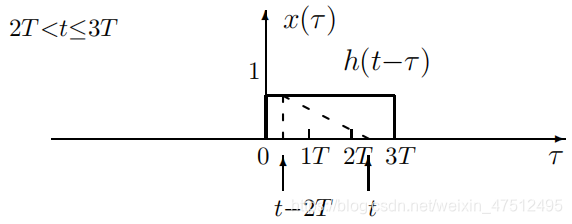
y(t)=∫t−2Ttx(τ)h(t−τ)dτ=12T∫t−2Tt(t−τ)dτ=Ty(t)=\int_{t-2T}^tx(\tau)h(t-\tau)d{\tau}=\cfrac1{2T}\int_{t-2T}^t(t-\tau)d{\tau}=Ty(t)=∫t−2Ttx(τ)h(t−τ)dτ=2T1∫t−2Tt(t−τ)dτ=T
情况4情况4情况4
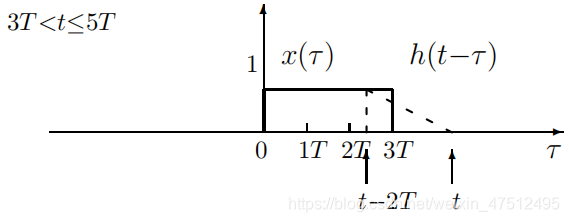
y(t)=∫t−2T3Tx(τ)h(t−τ)dτ=12T∫t−2T3T(t−τ)dτ=14T(−5T2+6tT−t2)y(t)=\int_{t-2T}^{3T}x(\tau)h(t-\tau)d{\tau}=\cfrac1{2T}\int_{t-2T}^{3T}(t-\tau)d{\tau}=\cfrac1{4T}(-5T^2+6tT-t^2)y(t)=∫t−2T3Tx(τ)h(t−τ)dτ=2T1∫t−2T3T(t−τ)dτ=4T1(−5T2+6tT−t2)
情况5情况5情况5
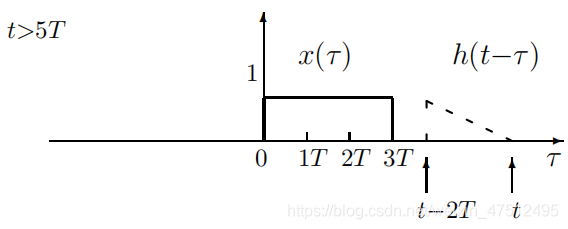
y(t)=0。y(t)=0。y(t)=0。
此外连续函数卷积还可以借助傅里叶变换、拉普拉斯变换、卷积的各种性质求解。此外连续函数卷积还可以借助傅里叶变换、拉普拉斯变换、卷积的各种性质求解。此外连续函数卷积还可以借助傅里叶变换、拉普拉斯变换、卷积的各种性质求解。
2.离散函数的卷积
2.1 表格法(Papierstreifenmethode)

当数列fn,hn和yn的长度分别为Lf,Lh和Ly时,那么Ly=Lf+Lh−1。当数列f_n,h_n和y_n的长度分别为L_f,L_h和L_y时,那么L_y=L_f+L_h-1。当数列fn,hn和yn的长度分别为Lf,Lh和Ly时,那么Ly=Lf+Lh−1。
2.2 借助冲激信号
Dirac−Implus δk(n)={1,n=00,其他
Dirac-Implus\ \delta_k(n)=
\begin{cases}
1, & n=0\\
0, &其他
\end{cases}
Dirac−Implus δk(n)={1,0,n=0其他
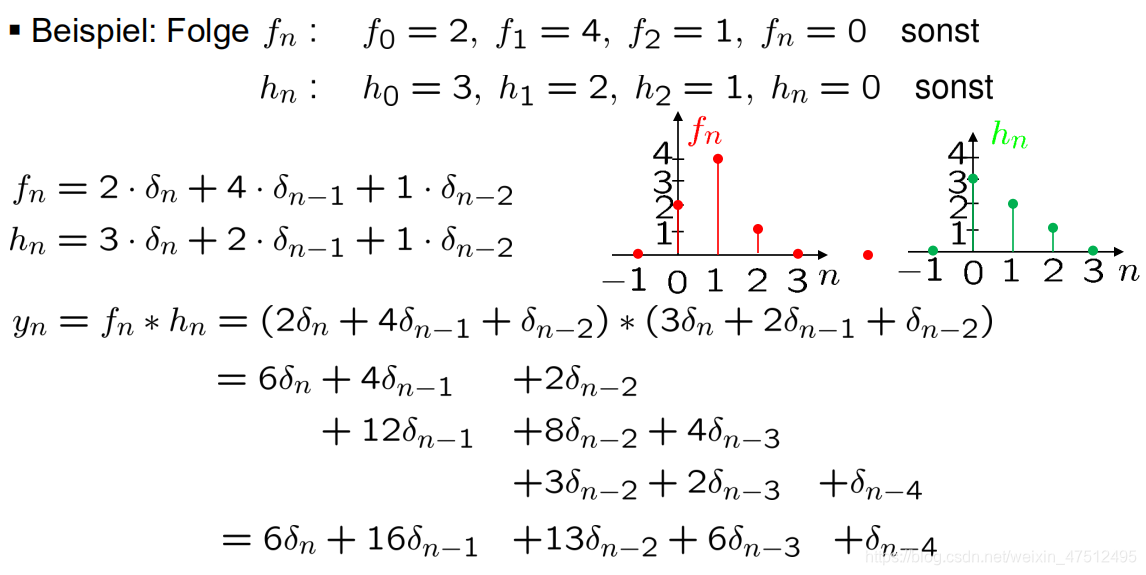
2.3 借助Z变换
单边Z变换,F(z)=单边Z变换,F(z)=单边Z变换,F(z)=∑n=0∞\sum_{n=0}^\infty∑n=0∞ fnz−nf_nz^{-n}fnz−n
Z{δ(n)}=1,延迟定理Z{fn−k}=z−k[F(z)+Z\{\delta(n)\}=1,延迟定理Z\{f_{n-k}\}=z^{-k}[F(z)+Z{δ(n)}=1,延迟定理Z{fn−k}=z−k[F(z)+∑m=1kf−mzm\sum_{m=1}^kf_{-m}z^m∑m=1kf−mzm]
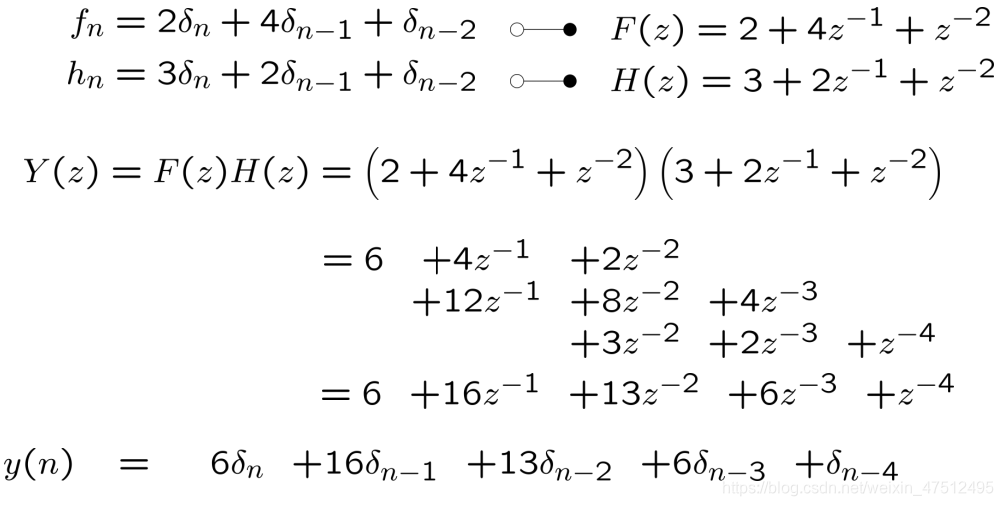
总结:设数列fn和hn分别通过连续信号f(t)和h(t)理想采样获得y(t)=f(t)∗h(t)≠yn=fn∗hn,因为在连续卷积中,采样点之间的函数值也会影响结果。总结:设数列f_n和h_n分别通过连续信号f(t)和h(t)理想采样获得y(t)=f(t)\ast h(t)\neq y_n=f_n\ast h_n,因为在连续卷积中,采样点之间的函数值也会影响结果。总结:设数列fn和hn分别通过连续信号f(t)和h(t)理想采样获得y(t)=f(t)∗h(t)=yn=fn∗hn,因为在连续卷积中,采样点之间的函数值也会影响结果。
2.3 循环卷积(Zyklische Faltung)
通常所说的卷积都为线性卷积(Lineare Faltung)两个函数的循环卷积是由他们的周期延伸所来定义的。通常所说的卷积都为线性卷积(Lineare\ Faltung)两个函数的循环卷积是由他们的周期延伸所来定义的。通常所说的卷积都为线性卷积(Lineare Faltung)两个函数的循环卷积是由他们的周期延伸所来定义的。周期延伸意思是把原本的函数平移某个周期T的整数倍后再全部加起来,所产生的新函数。循环卷积要借周期延伸意思是把原本的函数平移某个周期 T 的整数倍后再全部加起来,所产生的新函数。循环卷积要借周期延伸意思是把原本的函数平移某个周期T的整数倍后再全部加起来,所产生的新函数。循环卷积要借
助离散傅里叶变换(DFT)助离散傅里叶变换(DFT)助离散傅里叶变换(DFT)
x(n)∘—∙XDFT(k)x(n){\circ—\bullet} X_{DFT}(k)x(n)∘—∙XDFT(k)
ΔΩ=2πNWN=e−j2πN\Delta\Omega=\cfrac{2\pi}N \qquad\qquad\qquad\qquad W_N=e^{-j\cfrac{2\pi}N}ΔΩ=N2πWN=e−jN2π
XDFT(k)=∑n=0N−1x(n)e−jΔΩk⋅n=∑n=0N−1x(n)WNkn 只在k=0,1,...,N−1定义X_{DFT}(k)=\sum_{n=0}^{N-1}x(n)e^{-j\Delta\Omega k\cdot n}=\sum_{n=0}^{N-1}x(n)W_N^{kn} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 只在k=0,1,...,N-1定义XDFT(k)=∑n=0N−1x(n)e−jΔΩk⋅n=∑n=0N−1x(n)WNkn 只在k=0,1,...,N−1定义
























 4047
4047

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








