Python优化算法08——粘液霉菌算法

参考链接：http://www.alimirjalili.com/SMA.html

                  https://tinyurl.com/Slime-mould-algorithm.

---

这个优化算法是2020年提出来的，还算比较新的算法，上面两个链接都有源码。

本着能用的代码就是好代码的原则，我把人家的代码搬了过来组合了一下，测试后可以使用...

直接上代码

---

粘液霉菌算法（SMA）

这一段是定义优化算法一般的功能

from numpy import where, clip, logical_and, ones, array, ceil
from numpy.random import uniform, choice
from copy import deepcopy
from numpy import abs, zeros, log10, where, arctanh, tanh

class Root:
    """ This is root of all Algorithms """

    ID_MIN_PROB = 0         # min problem
    ID_MAX_PROB = -1        # max problem

    ID_POS = 0              # Position
    ID_FIT = 1              # Fitness

    EPSILON = 10E-10

    def __init__(self, obj_func=None, lb=None, ub=None, problem_size=50, verbose=True):
        """
        Parameters
        ----------
        obj_func : function
        lb : list
        ub : list
        problem_size : int, optional
        batch_size: int, optional
        verbose : bool, optional
        """
        self.obj_func = obj_func
        if (lb is None) or (ub is None):
            if problem_size is None:
                print("Problem size must be an int number")
                exit(0)
            elif problem_size <= 0:
                print("Problem size must > 0")
                exit(0)
            else:
                self.problem_size = int(ceil(problem_size))
                self.lb = -1 * ones(problem_size)
                self.ub = 1 * ones(problem_size)
        else:
            if isinstance(lb, list) and isinstance(ub, list) and not (problem_size is None):
                if (len(lb) == len(ub)) and (problem_size > 0):
                    if len(lb) == 1:
                        self.problem_size = problem_size
                        self.lb = lb[0] * ones(problem_size)
                        self.ub = ub[0] * ones(problem_size)
                    else:
                        self.problem_size = len(lb)
                        self.lb = array(lb)
                        self.ub = array(ub)
                else:
                    print("Lower bound and Upper bound need to be same length. Problem size must > 0")
                    exit(0)
            else:
                print("Lower bound and Upper bound need to be a list. Problem size is an int number")
                exit(0)
        self.verbose = verbose
        self.epoch, self.pop_size = None, None
        self.solution, self.loss_train = None, []

    def create_solution(self, minmax=0):
        """ Return the position position with 2 element: position of position and fitness of position
        Parameters
        ----------
        minmax
            0 - minimum problem, else - maximum problem
        """
        position = uniform(self.lb, self.ub)
        fitness = self.get_fitness_position(position=position, minmax=minmax)
        return [position, fitness]

    def get_fitness_position(self, position=None, minmax=0):
        """     Assumption that objective function always return the original value
        :param position: 1-D numpy array
        :param minmax: 0- min problem, 1 - max problem
        :return:
        """
        return self.obj_func(position) if minmax == 0 else 1.0 / (self.obj_func(position) + self.EPSILON)

    def get_sorted_pop_and_global_best_solution(self, pop=None, id_fit=None, id_best=None):
        """ Sort population and return the sorted population and the best position """
        sorted_pop = sorted(pop, key=lambda temp: temp[id_fit])
        return sorted_pop, deepcopy(sorted_pop[id_best])

    def amend_position(self, position=None):
        return clip(position, self.lb, self.ub)

    def amend_position_random(self, position=None):
        return where(logical_and(self.lb <= position, position <= self.ub), position, uniform(self.lb, self.ub))

    def update_sorted_population_and_global_best_solution(self, pop=None, id_best=None, g_best=None):
        """ Sort the population and update the current best position. Return the sorted population and the new current best position """
        sorted_pop = sorted(pop, key=lambda temp: temp[self.ID_FIT])
        current_best = sorted_pop[id_best]
        g_best = deepcopy(current_best) if current_best[self.ID_FIT] < g_best[self.ID_FIT] else deepcopy(g_best)
        return sorted_pop, g_best

下面是两种不同的SMA算法的类

class BaseSMA(Root):
    """
        Modified version of: Slime Mould Algorithm (SMA)
            (Slime Mould Algorithm: A New Method for Stochastic Optimization)
        Notes:
            + Selected 2 unique and random solution to create new solution (not to create variable) --> remove third loop in original version
            + Check bound and update fitness after each individual move instead of after the whole population move in the original version
    """
    ID_WEI = 2

    def __init__(self, obj_func=None, lb=None, ub=None, problem_size=50, verbose=True, epoch=750, pop_size=100, z=0.03):
        Root.__init__(self, obj_func, lb, ub, problem_size, verbose)
        self.epoch = epoch
        self.pop_size = pop_size
        self.z = z

    def create_solution(self, minmax=0):
        pos = uniform(self.lb, self.ub)
        fit = self.get_fitness_position(pos)
        weight = zeros(self.problem_size)
        return [pos, fit, weight]

    def train(self):
        pop = [self.create_solution() for _ in range(self.pop_size)]
        pop, g_best = self.get_sorted_pop_and_global_best_solution(pop, self.ID_FIT, self.ID_MIN_PROB)      # Eq.(2.6)

        for epoch in range(self.epoch):

            s = pop[0][self.ID_FIT] - pop[-1][self.ID_FIT] + self.EPSILON  # plus eps to avoid denominator zero

            # calculate the fitness weight of each slime mold
            for i in range(0, self.pop_size):
                # Eq.(2.5)
                if i <= int(self.pop_size / 2):
                    pop[i][self.ID_WEI] = 1 + uniform(0, 1, self.problem_size) * log10((pop[0][self.ID_FIT] - pop[i][self.ID_FIT]) / s + 1)
                else:
                    pop[i][self.ID_WEI] = 1 - uniform(0, 1, self.problem_size) * log10((pop[0][self.ID_FIT] - pop[i][self.ID_FIT]) / s + 1)

            a = arctanh(-((epoch + 1) / self.epoch) + 1)                        # Eq.(2.4)
            b = 1 - (epoch + 1) / self.epoch

            # Update the Position of search agents
            for i in range(0, self.pop_size):
                if uniform() < self.z:  # Eq.(2.7)
                    pos_new = uniform(self.lb, self.ub)
                else:
                    p = tanh(abs(pop[i][self.ID_FIT] - g_best[self.ID_FIT]))    # Eq.(2.2)
                    vb = uniform(-a, a, self.problem_size)                      # Eq.(2.3)
                    vc = uniform(-b, b, self.problem_size)

                    # two positions randomly selected from population, apply for the whole problem size instead of 1 variable
                    id_a, id_b = choice(list(set(range(0, self.pop_size)) - {i}), 2, replace=False)

                    pos_1 = g_best[self.ID_POS] + vb * (pop[i][self.ID_WEI] * pop[id_a][self.ID_POS] - pop[id_b][self.ID_POS])
                    pos_2 = vc * pop[i][self.ID_POS]
                    pos_new = where(uniform(0, 1, self.problem_size) < p, pos_1, pos_2)

                # Check bound and re-calculate fitness after each individual move
                pos_new = self.amend_position(pos_new)
                fit_new = self.get_fitness_position(pos_new)
                pop[i][self.ID_POS] = pos_new
                pop[i][self.ID_FIT] = fit_new

            # Sorted population and update the global best
            pop, g_best = self.update_sorted_population_and_global_best_solution(pop, self.ID_MIN_PROB, g_best)
            self.loss_train.append(g_best[self.ID_FIT])
            if self.verbose:
                print("> Epoch: {}, Best fit: {}".format(epoch + 1, g_best[self.ID_FIT]))
        self.solution = g_best
        return g_best[self.ID_POS], g_best[self.ID_FIT], self.loss_train


class OriginalSMA(Root):
    """
        The original version of: Slime Mould Algorithm (SMA)
            (Slime Mould Algorithm: A New Method for Stochastic Optimization)
        Link:
            https://doi.org/10.1016/j.future.2020.03.055
    """

    ID_WEI = 2

    def __init__(self, obj_func=None, lb=None, ub=None, problem_size=50, verbose=True, epoch=750, pop_size=100, z=0.03):
        Root.__init__(self, obj_func, lb, ub, problem_size, verbose)
        self.epoch = epoch
        self.pop_size = pop_size
        self.z = z

    def create_solution(self, minmax=0):
        pos = uniform(self.lb, self.ub)
        fit = self.get_fitness_position(pos)
        weight = zeros(self.problem_size)
        return [pos, fit, weight]

    def train(self):
        pop = [self.create_solution() for _ in range(self.pop_size)]
        pop, g_best = self.get_sorted_pop_and_global_best_solution(pop, self.ID_FIT, self.ID_MIN_PROB)      # Eq.(2.6)

        for epoch in range(self.epoch):

            s = pop[0][self.ID_FIT] - pop[-1][self.ID_FIT] + self.EPSILON       # plus eps to avoid denominator zero

            # calculate the fitness weight of each slime mold
            for i in range(0, self.pop_size):
                # Eq.(2.5)
                if i <= int(self.pop_size / 2):
                    pop[i][self.ID_WEI] = 1 + uniform(0, 1, self.problem_size) * log10((pop[0][self.ID_FIT] - pop[i][self.ID_FIT]) / s + 1)
                else:
                    pop[i][self.ID_WEI] = 1 - uniform(0, 1, self.problem_size) * log10((pop[0][self.ID_FIT] - pop[i][self.ID_FIT]) / s + 1)

            a = arctanh(-((epoch + 1) / self.epoch) + 1)                        # Eq.(2.4)
            b = 1 - (epoch + 1) / self.epoch

            # Update the Position of search agents
            for i in range(0, self.pop_size):
                if uniform() < self.z:                                          # Eq.(2.7)
                    pop[i][self.ID_POS] = uniform(self.lb, self.ub)
                else:
                    p = tanh(abs(pop[i][self.ID_FIT] - g_best[self.ID_FIT]))    # Eq.(2.2)
                    vb = uniform(-a, a, self.problem_size)                      # Eq.(2.3)
                    vc = uniform(-b, b, self.problem_size)
                    for j in range(0, self.problem_size):
                        # two positions randomly selected from population
                        id_a, id_b = choice(list(set(range(0, self.pop_size)) - {i}), 2, replace=False)
                        if uniform() < p:  # Eq.(2.1)
                            pop[i][self.ID_POS][j] = g_best[self.ID_POS][j] + vb[j] * (
                                        pop[i][self.ID_WEI][j] * pop[id_a][self.ID_POS][j] - pop[id_b][self.ID_POS][j])
                        else:
                            pop[i][self.ID_POS][j] = vc[j] * pop[i][self.ID_POS][j]

            # Check bound and re-calculate fitness after the whole population move
            for i in range(0, self.pop_size):
                pos_new = self.amend_position(pop[i][self.ID_POS])
                fit_new = self.get_fitness_position(pos_new)
                pop[i][self.ID_POS] = pos_new
                pop[i][self.ID_FIT] = fit_new

            # Sorted population and update the global best
            pop, g_best = self.update_sorted_population_and_global_best_solution(pop, self.ID_MIN_PROB, g_best)
            self.loss_train.append(g_best[self.ID_FIT])
            if self.verbose:
                print("> Epoch: {}, Best fit: {}".format(epoch + 1, g_best[self.ID_FIT]))
        self.solution = g_best
        return g_best[self.ID_POS], g_best[self.ID_FIT], self.loss_train

定义问题参数，可以定义任意自己想优化的问题，寻找最小值

#from SMA import BaseSMA, OriginalSMA
#from numpy import sum, pi, exp, sqrt, cos
import numpy as np

## You can create whatever function you want here
def func_sum(solution):
    return np.sum(solution ** 2)

def func_ackley(solution):
    a, b, c = 20, 0.2, 2 * np.pi
    d = len(solution)
    sum_1 = -a * np.exp(-b * np.sqrt(np.sum(solution ** 2) / d))
    sum_2 = np.exp(np.sum(np.cos(c * solution)) / d)
    return sum_1 - sum_2 + a + np.exp(1)

## You can create different bound for each dimension like this
# lb = [-15, -10, -3, -15, -10, -3, -15, -10, -3, -15, -10, -3, -15, -10, -3, -100, -40, -50]
# ub = [15, 10, 3, 15, 10, 3, 15, 10, 3, 15, 10, 3, 15, 10, 3, 20, 200, 1000]
# problem_size = 18
## if you choose this way, the problem_size need to be same length as lb and ub

## Or bound is the same for all dimension like this
lb = [-100]
ub = [100]
problem_size = 100
## if you choose this way, the problem_size can be anything you want


## Setting parameters
obj_func = func_ackley
verbose = True
epoch = 100
pop_size = 50

开始使用两种SMA进行测试

第一种基础的SMA

md1 = BaseSMA(obj_func, lb, ub, problem_size, verbose, epoch, pop_size)
best_pos1, best_fit1, list_loss1 = md1.train()
# return : the global best solution, the fitness of global best solution and the loss of training process in each epoch/iteration
print(md1.solution[0])
print(md1.solution[1])
#print(md1.loss_train)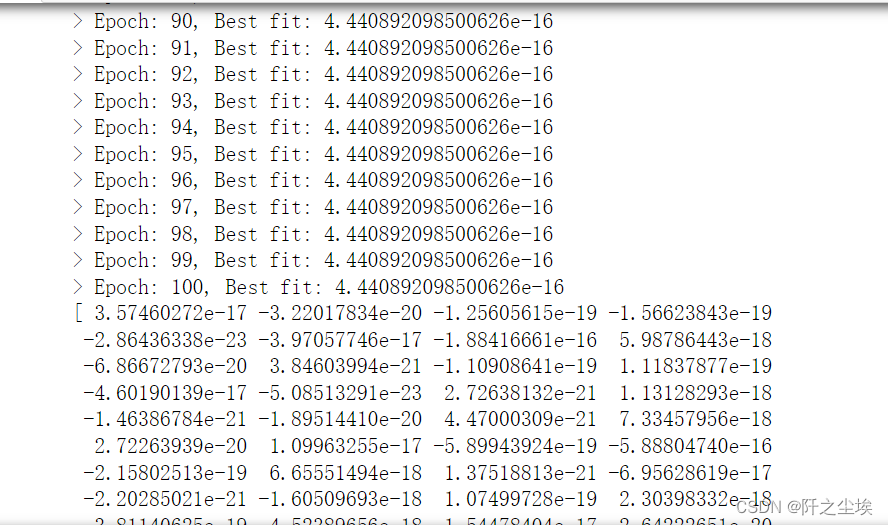

 verbose开着的话会显示每轮迭代的损失的大小，md1.solution[0]打印最优的X，md1.solution[1]打印最优的y值。

md1.loss_train可以返回每轮迭代的损失y的变化，是一个数组，画图什么很方便。

---

第二种SMA

md2 = OriginalSMA(obj_func, lb, ub, problem_size, verbose, epoch, pop_size)
best_pos2, best_fit2, list_loss2 = md2.train()
# return : the global best solution, the fitness of global best solution and the loss of training process in each epoch/iteration
print(best_pos2)
print(best_fit2)
#print(list_loss2)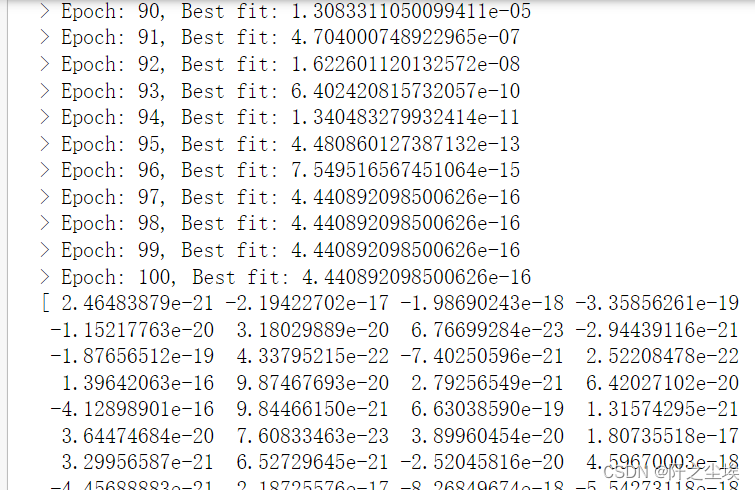

 返回值都差不多，但是这种SMA 的运行时间有点略微的长，想来是更加复杂点。

---

如有兴趣研究原理的同学可以进下面的链接，是这篇算法的论文的链接。

Paper:https://doi.org/10.1016/j.future.2020.03.055