#训练2# 3-最短工期

题目

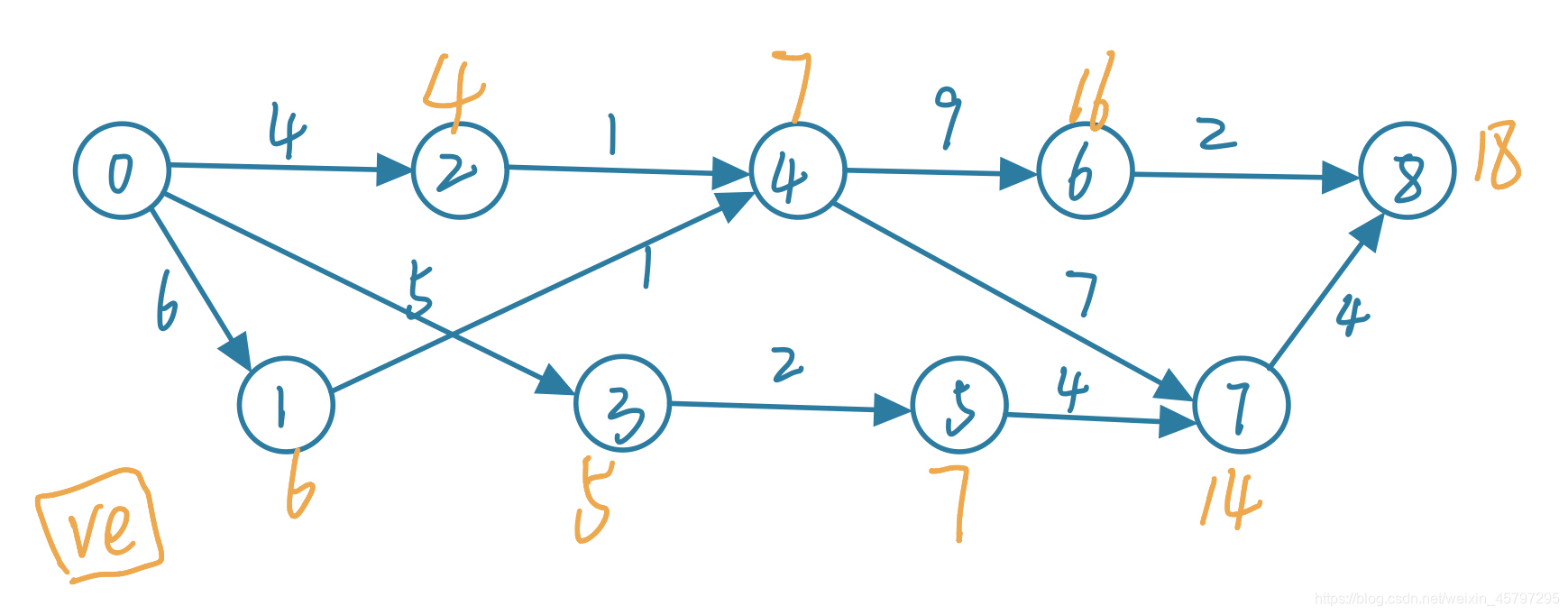
思路

拓扑排序~
拓扑排序的实现可以用到一个栈（记录有哪几个点被标记过，判断是否有环），一个队列（找顺序的）
因为在排序的过程中，需要不断地用到from和to的信息，所以用结构体来存储的话，并不方便；用vector跟便于查找（当然也可以sort一下？？），感觉自己stl用的还不熟练灵活（/_ \）

代码

#include <iostream>
#include <cstring>
#include <stack>
#include <algorithm>
#include <queue>
#define MAXX 10100
using namespace std;
vector<pair<int,int>> road[MAXX];
int in[MAXX],ve[MAXX];
int n,m;

bool topsort()
{
    queue<int> q;
    stack<int> st;
    for (int i = 0; i < n; ++i)
    {
        if (in[i] == 0)
            q.push(i);
    }
    while (!q.empty() )
    {
        int from = q.front();
        q.pop();
        st.push(from);
        for (int i = 0; i < road[from].size(); ++i)
        {
            int to = road[from][i].first;
            in[to]--;
            if (in[to] == 0)
                q.push(to);
            if (ve[from] + road[from][i].second > ve[to])
                ve[to] = ve[from]+road[from][i].second;
        }
    }
    if (st.size()==n)
        return true;
    return false;
}

int main()
{
    cin>>n>>m;
    while (m--)
    {
        int a,b,c;
        cin>>a>>b>>c;
        road[a].push_back(make_pair(b,c));
        in[b]++;
    }
    int ans = -1;
    if (topsort())  //如果是有向无环图
    {
        for (int i = 0; i < n; ++i)
        {
            //cout<<ve[i]<<' ';
            ans = max(ans,ve[i]);
        }
        cout<<ans<<endl;
    }
    else
        cout << "Impossible" << endl;
    return 0;
}

注意

这是一份完整的可以求关键路径的代码

#include<iostream>
#include<string>
#include<vector>
#include<queue>
#include<stack>
using namespace std;
const int MAXV = 105;
vector<pair<int, int> > g[MAXV];//图,first为后继点，second为边长
int n, m;
int indegree[MAXV] = { 0 };//每个点的入度
int ve[MAXV] = { 0 };//最早发生时间
int vl[MAXV];
stack<int> toporder;//入度为0的点出队时依次进栈
int criticalpath() {//计算最晚发生时间和输出关键活动，返回关键路径长度，适用于汇点确定且唯一的情况
	fill(vl, vl + n, ve[n - 1]);//vl数组初始化为汇点的ve值
	//直接使用toporder出栈即为逆拓扑序列，求解vl数组
	while (!toporder.empty()) {
		int u = toporder.top();
		toporder.pop();
		for (int i = 0; i < g[u].size(); i++) {
			int v = g[u][i].first;//u的后继结点
			//用u的所有后继结点v的vl值来更新vl[u]
			if (vl[v] - g[u][i].second < vl[u]) {
				vl[u] = vl[v] - g[u][i].second;
			}
		}
	}
	//上面计算最晚发生时间，下面输出关键活动
	//遍历邻接表的所有边，计算活动的最早发生时间与最迟开始时间
	for (int u = 0; u < n; u++) {
		for (int i = 0; i < g[u].size(); i++) {
			int v = g[u][i].first, w = g[u][i].second;
			//e活动最早开始时间，l活动最晚发生时间
			int e = ve[u], l = vl[v] - w;
			//e==l说明，活动u->v是关键活动
			if (e == l)cout << u << "->" << v << endl;
		}
	}
	return ve[n - 1];//返回关键路径长度
}
bool toplogicalsort() {
	queue<int> q;
	for (int i = 0; i < n; i++) {//入度为0的点进队
		if (indegree[i] == 0)q.push(i);
	}
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		toporder.push(u);
		for (int i = 0; i < g[u].size(); i++) {
			int v = g[u][i].first;//记录此后继结点
			indegree[v]--;//后继点入度减1
			if (indegree[v] == 0)q.push(v);//后继点入度为0时入队
 
			if (ve[u] + g[u][i].second > ve[v])//最早发生时间取最大值
				ve[v] = ve[u] + g[u][i].second;
		}
	}
	if (toporder.size() == n)return true;//如果有n个结点，说明是有向无环图
	else return false;
}
int main() {
	cin >> n >> m;
	int a, b, c;
	while (m--) {
		cin >> a >> b >> c;
		g[a].push_back(make_pair(b, c));
		indegree[b]++;
	}
	if (toplogicalsort()) {//有多个终点时
		int k = 0;
		for (int i = 0; i < n; i++)
			k = max(k, ve[i]);
		cout << k << endl;
	}
	else cout << "Impossible" << endl;
	//criticalpath();计算最晚发生时间，输出关键路径，返回关键路径长度
}