拓扑排序

1. 用顶点表示活动的网络（AOV）

在干工程的时候，比如施工过程、生产过程、程序流程，都会把一个大工程分为好几个小工程，一步一步来，当小工程完成后，大工程也就完成了~

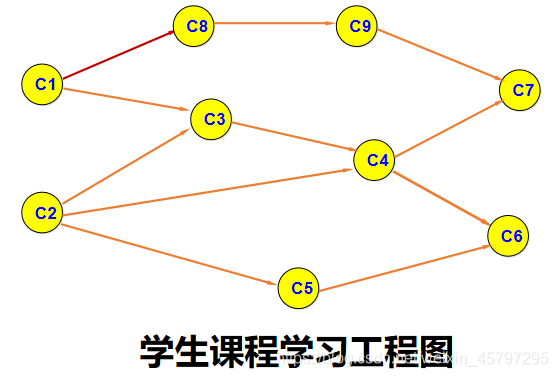
可以用一个有向图来存储这些过程，在这种有向图中，用顶点表示活动，用有向边$<Vi,Vj>$表示活动Vi 必须先于活动Vj 进行。这种有向图叫做顶点表示活动的AOV网络 (Activity On Vertices)

//注意：AOV网络中不能出现有向环
*用拓扑排序检测有向环

1.1 拓扑排序

把一个非线性的关系转换成为线性关系，是一个有向无环图

1.1.1 基本思想

1. 在有向无环图中，找到入度为0的节点，输出，并删除此节点和此节点的出度（使用queue）
2. 依次找到所有符合节点
3. 判断所有节点是否都已输出，全部输出则结束
   

1.1.2 题目

1.确定比赛排名
2.老板发红包

2. 用边表示活动的网络（AOE）

//就是AOV网络上，边有了权值

2.1 概念

如果在无有向环的带权有向图中, 用有向边表示一个工程中的活动 (Activity), 用边上权值表示活动持续时间 (Duration), 用顶点表示事件 (Event), 则这样的有向图叫做用边表示活动的网络, 简称 AOE ( Activity On Edges ) 网络

2.2 关键路径

• 完成整个工程所需的时间 == 从起点到终点的最长路径，也叫关键路径
• 要找出关键路径，必须找出关键活动, 即不按期完成就会影响整个工程完成的活动。
• 关键路径上的所有活动都是关键活动。因此, 只要找到了关键活动, 就可以找到关键路径。
  与关键活动有关的几个量：
  ① 事件V_i最早开始时间$Ve[i]$，注意这里是在整个工程里的，从前往后推
  ② 事件V_i最迟开始时间$Vl[i]$，从后往前推
  如果，最早开始时间 == 最迟开始时间，那么就是关键活动
  以上面的图片为例，求关键路径：
  

2.3 题目

有两类，一类是直接输出时间的，一类是要输出关键路径的
1. 最短工期