Ceres中LocalParameterization参数Jacobian矩阵计算过程

Ceres中有一些变量实际的自由度比自身维度要低。例如四元数维度为4，其实际自由度为3。对于这类变量，Ceres在优化这类变量时，会定义一个LocalParameterization（新版为Manifold）来更新变量。
这类变量有两种空间，一种是流形空间Manifold（GlobalSize)，另一种是切空间Tangent(LocalSize)。例如四元数为Manifold空间维度为4，Tangent空间为3。Ceres在Evaluate函数中定义了一个jacobian矩阵（定义为J1),然后再LocalParameterization中ComputeJacobian函数中又定义了一个jacaobian矩阵(定义为J2)。其中J1是残差对Manifold变量求导，J2是Manifold是对Tangent变量求导。根据链式法则，J1*J2是残差实际更新的jacobian矩阵。

以四元数为例，QuaternionParameterization 的方法 bool ComputeJacobian(const double* x, double* jacobian) 计算得到一个 4x3 的矩阵。这些由 ComputeJacobian 计算得到的矩阵在 ceres 代码中被称作 “global_to_local”，含义是 Manifold 上变量对 Tangent Space 上变量的导数。在 ceres::CostFunction 处提供 residuals 对 Manifold 上变量的导数:$$\frac{\partial e}{\partial X^G}$$

乘以Manifold 上变量对 Tangent Space 上变量的导数$$\frac{\partial X^G}{\partial X^L}$$

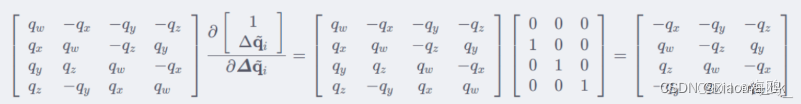
根据链式法则变成残差对 Tangent Space 上变量的导数,这个导数就是最终用于计算梯度的jacobian矩阵:$$\frac{\partial e}{\partial X^L}=\frac{\partial e}{\partial X^G}\frac{\partial X^G}{\partial X^L}$$。
上述一些基础概念以及公式推导的一些细节可以参考下述三个链接：
[ceres-solver] From QuaternionParameterization to LocalParameterization
vins estimator PoseLocalParameterization
【Ceres】（二）LocalParameterization参数化