第12章 几何图元
矩形边界框 矩形边界框的限制是:边必须垂直于坐标轴,称为AABB(axially aligned bounding box轴对齐矩形边界框)
OOB oriented bounding box(方向矩形边界框)
AABB表示方法
-
首先AABB满足一下条件
xmin<=x<=xmaxx_{min}<=x<=x_{max}xmin<=x<=xmax
ymin<=y<=ymaxy_{min}<=y<=y_{max}ymin<=y<=ymax
zmin<=z<=zmaxz_{min}<=z<=z_{max}zmin<=z<=zmax
pmin=[xmin,ymin,zmin]p_{min}=[x_{min},y_{min},z_{min}]pmin=[xmin,ymin,zmin]
pmax=[xmax,ymax,zmax]p_{max}=[x_{max},y_{max},z_{max}]pmax=[xmax,ymax,zmax] -
中心点c
c=(pmin+pmax)/2c=(p_{min}+p_{max})/2c=(pmin+pmax)/2 -
尺寸向量,包含了矩形的长、宽、高
s=pmax−pmaxs=p_{max}-p_{max}s=pmax−pmax -
半径向量
r=pmax−c=s/2r=p_{max}-c=s/2r=pmax−c=s/2
计算AABB
- 计算AABB只要计算出pmin和pmaxp_{min}和p_{max}pmin和pmax就可以通过上面的公式算出有用的信息
- pmin和pmaxp_{min}和p_{max}pmin和pmax如何计算?只需要将pmin和pmaxp_{min}和p_{max}pmin和pmax设为无穷大和无穷小,然后通过遍历所有点,通过比较扩展pmin和pmaxp_{min}和p_{max}pmin和pmax
代码后面补
AABB和边界球
- 首先计算边界球比AABB编程上复杂的多
- 边界球只有一个自由度:半径,而AABB有三个自由度:长、宽、高,并且边界球对于方向并不敏感,比如一个棍子,处于不同方向,此时边界球是相同的,但是AABB却是不同的
AABB变换
- 当物体移动后,AABB也需要进行变换,AABB有pmin和pmaxp_{min}和p_{max}pmin和pmax,我们只需要计算出移动后的pmin和pmaxp_{min}和p_{max}pmin和pmax,点变换如下图
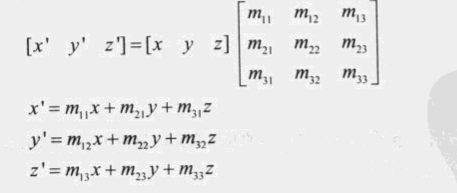
- 所以需要求出x’,y’,z’的最大值和最小值即可,举例比如x’最小值,当m11>0m_{11}>0m11>0时使用xminx_{min}xmin计算最小值,使用xmaxx_{max}xmax计算最大值,其他同理,具体代码如下
代码后面补
平面
- 平面的2种记法,其中n为法向量垂直于平面,
法向量指向的方向是平面的正方向(我们看向平面正面,法向量将指向我们)
ax + by + cz = d
p · n = d
如何计算出n法向量呢?
取平面上3个点(不在同一条线上,且顺时针),叉乘公式是sin在同一条直线的话叉乘结果为0,顺时针是因为左手坐标系顺时针的法向量是正面组成e1e_1e1和e2e_2e2向量,使用e1e_1e1叉乘e2e_2e2可以得到法向量,但是这不是单位向量,所以需要除以模,最后公式为
e1×e2∣e1×e2∣e_1\times e_2 \over |e_1\times e_2|∣e1×e2∣e1×e2
计算点集的最佳平面法向量
希望从一组3个以上的点集出平面方程,因为上面说了,可能出现在一条直线上,或者没有顺时针,下面有计算公式可以计算出最佳的的法向量如下

代码后面补
点到平面的距离
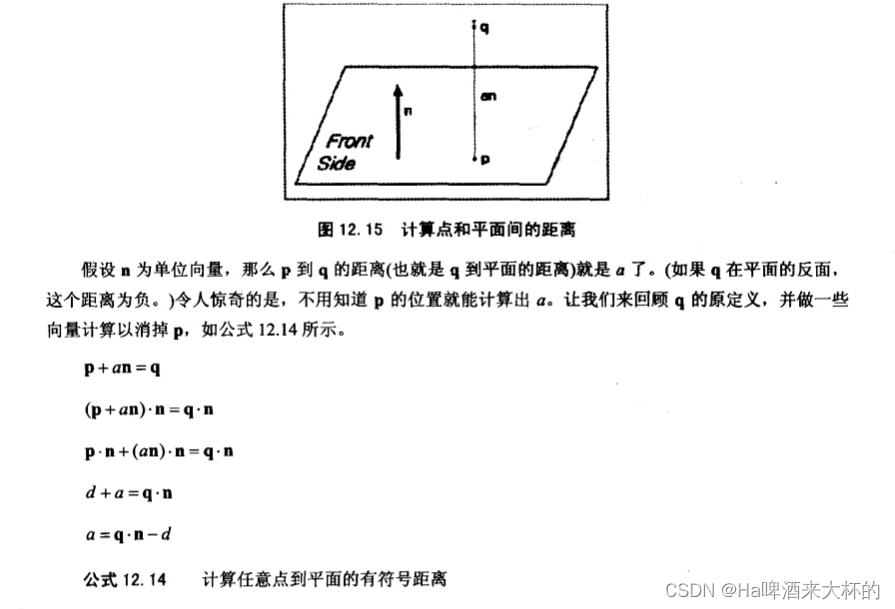
三角形
-
三角形面积
低乘高除以2,不知道h高,可以使用海伦公式计算
s=l1+l2+l32s = {l_1 + l_2 + l_3 \over 2}s=2l1+l2+l3
h=s(s−l1)(s−l2)(s−l3)2h = { \sqrt[2]{s(s-l_1)(s-l_2)(s-l_3)}}h=2s(s−l1)(s−l2)(s−l3) -
还有一种更加简洁的公式
A=∣∣e1×e2∣∣2A = { ||e_1 \times e_2|| \over 2}A=2∣∣e1×e2∣∣
A=(y1−y3)(x2−x3)+(y2−y3)(x3−x1)2A = { (y_1-y_3)(x_2-x_3)+(y_2-y_3)(x_3-x_1) \over 2}A=2(y1−y3)(x2−x3)+(y2−y3)(x3−x1)
重心坐标空间
定义:有一个坐标空间与三角形平面相关联且独立于三角形所在的3D坐标空间重心坐标三角形所在平面的任意点都能表示为顶点的加权平均值,这个权就称为重心坐标(b1,b2,b3)(b1, b2, b3)(b1,b2,b3)- b1+b2+b3=1b1+b2+b3 = 1b1+b2+b3=1
- 三角形3个顶点的重心坐标是单位向量
- 顶点的相对边上所有的点的重心坐标分量为0,v1顶点相对边上所有的重心坐标分量a1=0a1 = 0a1=0
- 该平面所有点都可以用重心坐标描述,该三角形内坐标在0~1之间,三角形外至少有一个分量为负,
重心坐标用和原来三角形大小相同的块铺满整个平面如下图
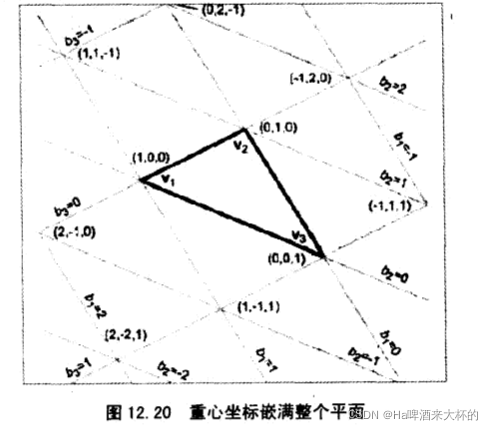
- 如何求得重心坐标呢?书中给了公式,如下图,注意P是这个平面内任意点

- 在3D中计算重心坐标更为复杂,因为p可能不在三角形平面中,这时是重心坐标是没有意义的,具体做法就是抛弃某一个分量,因为重心坐标计算最终就是计算三角形面积,垂直投影的面积是最大的,所以需要找到,最接近最大面积的投影,
这里可以通过检查平面法向量,看哪个分量值最大得到需要抛弃的分量
通过抛弃最大面积分量计算3D平面的重心坐标
代码后面补,这个不一定补
- 上面计算重心坐标很复杂,还有一种简单的方式计算重心坐标,根据上面计算三角形面积公式,可以知道三角形面积可以通过叉乘来计算
这里有个问题,叉乘的大小对顶点的顺序不敏感,总是正的,无法表示三角形外的重心坐标,因为三角形外的重心坐标总是有一个分量是负的,我们可以通过点乘,如下公式
c⋅n=∣∣c∣∣∣∣n∣∣cosθc·n = ||c||||n|| cos\thetac⋅n=∣∣c∣∣∣∣n∣∣cosθ首先让叉乘结果c点乘单位法向量n
c⋅n=∣∣c∣∣∗1∗(±1)c·n = ||c||*1*(±1)c⋅n=∣∣c∣∣∗1∗(±1)因为单位法向量和叉乘结果平行但是方向可能相反 相同时cos=1,不同时cos=-1
此时叉乘大小拥有了正负,具体推导如下图


三角形特殊点
重心是三角形的最佳平衡点,计算公式如下
G=v1+v2+v32G = {v_1+v_2+v_3\over2}G=2v1+v2+v3内心是三角形内切圆的圆心,与三条边l1、l2、l3l_1、l_2、l_3l1、l2、l3的距离相同,计算公式如下,p是周长
C=l1v1+l2v2+l3v3pC = {l_1v_1+l_2v_2+l_3v_3\over p}C=pl1v1+l2v2+l3v3
内心坐标快速计算公式如下
C=(l1p,l2p,l3p)C = ({l_1\over p},{l_2\over p},{l_3\over p})C=(pl1,pl2,pl3)
内心半径计算公式如下
R=ApR = {A\over p}R=pA
内心解决了寻找与三条边相切的圆外心是三角形外接圆圆心,是各个边垂直平分线的交点,计算思路可以通过重心坐标来计算
计算推导后面推
多边形
多边形有很多,复杂多边形有洞,可以通过在复杂多边形添加缝来将复杂多边形变为简单多边形三角形分解和扇形分解多边形可以分解为三角形,这样所有三角形操作都可以应用于此








 本文介绍了几何图元的基础概念,包括轴对齐矩形边界框(AABB)和方向矩形边界框(OBB)的表示方法及其计算过程。此外,还详细讲解了平面、三角形的性质及计算方法,如三角形面积计算、重心坐标空间的概念及其应用。
本文介绍了几何图元的基础概念,包括轴对齐矩形边界框(AABB)和方向矩形边界框(OBB)的表示方法及其计算过程。此外,还详细讲解了平面、三角形的性质及计算方法,如三角形面积计算、重心坐标空间的概念及其应用。
















 805
805

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








