浅谈DFS序

DFS序是什么

定义：树的dfs序是一个序列(可以类比前序序列等)，顾名思义，就是在按照dfs时搜到的顺序得到的序列

比如说，来张图

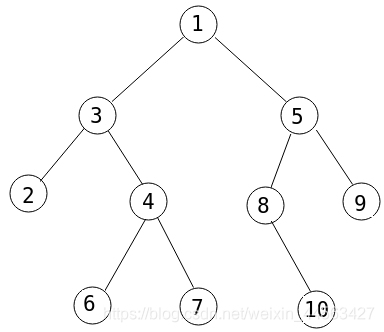
上面这棵树的dfs序为：1 3 2 4 6 7 5 8 10 9

为什么是DFS序

大家可能在想把一棵树转化成一个序列有什么用，在回答这一问题之前，我们先看看dfs序它有什么有用的性质。可以发现，节点$u$的子树在dfs序中为一段连续的区间，那利用dfs序就可以把对子树的操作转化为对区间的操作。对于子树，我们可能没有很有效的数据结构能够快速对其修改、查询等只是本蒟蒻没有，但是对于区间，我们可以用线段树、树状数组等数据结构其他也不会来快速修改、查询，前提是我们知道每个节点$u$的子树在dfs序上的区间的左右端点，左右端点其实很好求，左端点是第一次访问该点时记录，右端点是从该点离开时记录

代码

dfs序的思想很容易理解，代码也很短但是加上线段树就有点长

解释一下下面的变量都是个啥：

• $vis[i]$表示节点$i$是否被访问过
• $dfn[]$为dfs序
• $l[i],r[i]$为左右端点，代表节点$i$的子树在dfs序上的区间

// 直接拿vector存双向边，懒得写前向星，节点编号和区间从0开始的话请将len初始为-1
void dfs(int u) {
	vis[u] = 1;
	dfn[++len] = u;
	l[u] = len;
	int sz = g[u].size();
	for (int i = 0; i < sz; i++)
		if(!vis[g[u][i]])
			dfs(g[u][i]);
	r[u] = len;
}

例题

• POJ 3321 Apple Tree

  题意：给一棵有$n$个节点带权值的树和$m$次操作，节点权值一开始都是1，每次操作要么将一个节点的值取反，要么询问节点$u$的子树的权值和

  思路：板子题，用dfs序转化为单点修改+区间查询，树状数组就能做，又快又好写空间还小

• HDU_5692 Snacks

  题意：给一棵$n$个节点带权值的树和$m$次操作，每次操作要么修改一个点的权值，要么询问从根节点0开始经过节点$u$的路径中的权值和最大(不能往回走)

  思路：利用dfs序转化为区间操作，建一棵线段树，线段树的每个节点存储到达区间内的节点的路径的权值最大值，对于修改操作，相当于区间加，只不过加数是$val-$原来权值；询问就是求询问区间最大；别忘了打懒标记，不打可能超时

  模拟一下可能会好理解一些，还是上面那张图

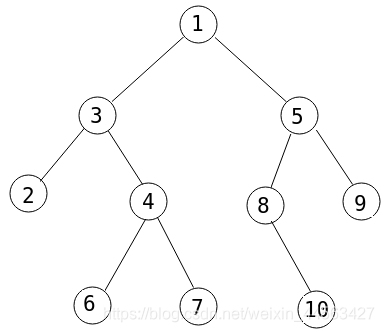
用dfs序建出的线段树如下(图中的标号不是下标

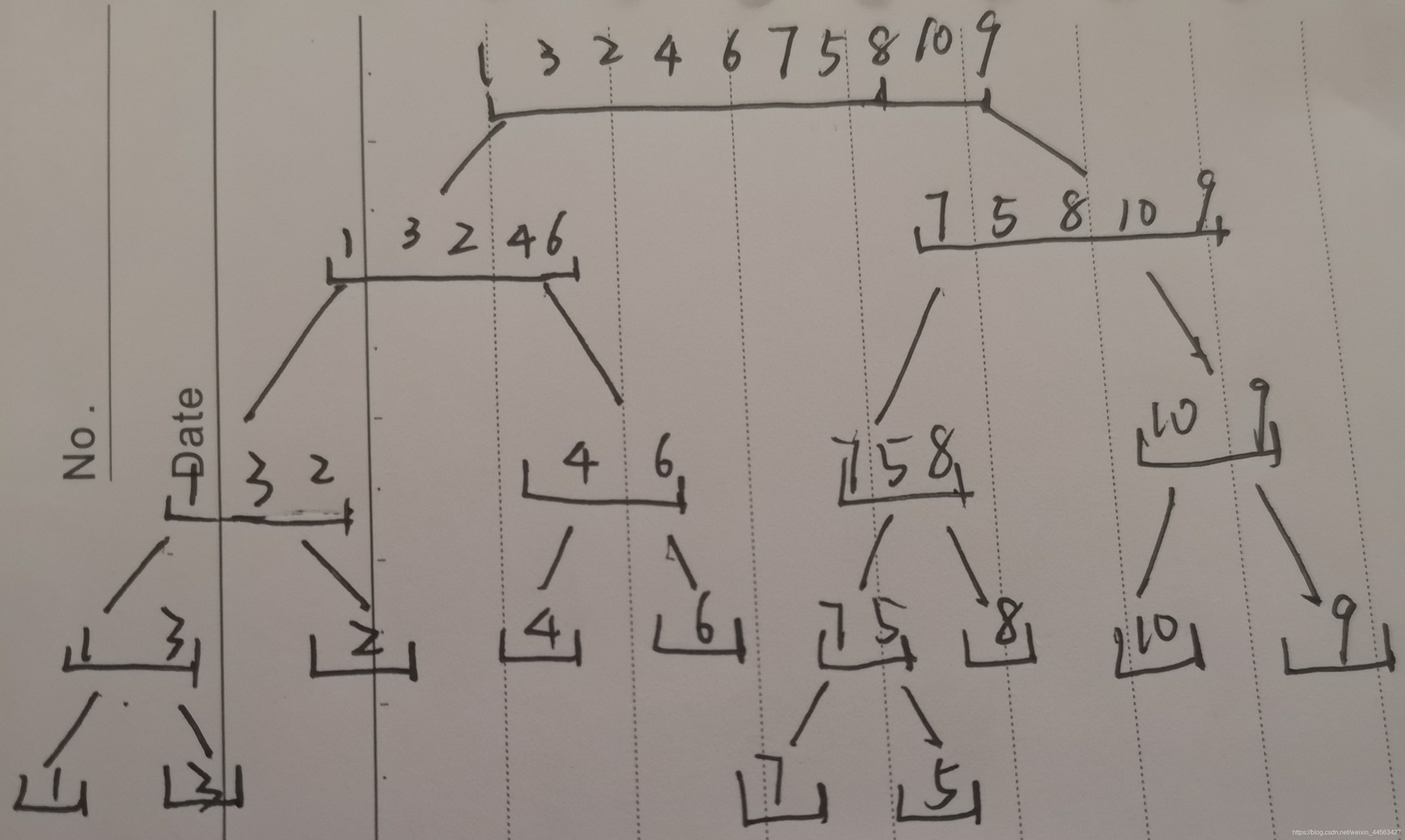
比如要修改节点4的权值，节点4的区间(从0开始)为$[3,5]$，从根节点开始向下模拟；查询包含节点4的路径的最大值时，也是区间$[3,5]$，从根节点往下就行了

细节看代码

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#define ls (k << 1)
#define rs (ls | 1)
typedef long long ll;
const int N = 1e5 + 5;
const ll INF = 1e18;

inline ll max(ll x, ll y) { return x > y ? x : y; }

struct Node {
    int l, r;
    ll ma, lazy;
    Node() {}
    Node(int l, int r, ll ma=0L, ll lazy=0L) : l(l), r(r), ma(ma), lazy(lazy) {}
}node[N << 2];

struct Edge {
    int v, nxt;
}e[N << 1];

int n, m, x, y, len, cnt;
int dfn[N], left[N], right[N], head[N];
ll sum[N], num[N], val, ans; // num[i]为节点i的权值，sum为从0开始到节点i的权值和
bool vis[N];

inline void init() {
    for(int i = 0; i < n; i++)
        head[i] = -1, vis[i] = 0;
    len = -1;
    cnt = val = 0;
}

inline void add(int u, int v) {
    e[cnt] = Edge{v, head[u]};
    head[u] = cnt++;
}

void dfs(int u) {
    vis[u] = 1;
    int x = len + 1;
    dfn[++len] = u;
    left[u] = len;
    for(int i = head[u]; i != -1; i = e[i].nxt) {
        int v = e[i].v;
        if(!vis[v]) {
            sum[v] += sum[u];
            dfs(v);
        }
    }
    right[u] = len;
}

inline void update(int k) {
    node[k].ma = max(node[ls].ma, node[rs].ma);
}

inline void push(int k) {
    if(node[k].lazy) {
        node[ls].lazy += node[k].lazy;
        node[rs].lazy += node[k].lazy;
        node[ls].ma += node[k].lazy;
        node[rs].ma += node[k].lazy;
        node[k].lazy = 0;
    }
}

void build(int l, int r, int k) {
    node[k] = Node(l, r);
    if(l == r) {
        node[k].ma = sum[dfn[l]];
        return ;
    }
    int mid = (l + r) >> 1;
    build(l, mid, ls);
    build(mid + 1, r, rs);
    update(k);
}

void change(int k) {
    if(node[k].l >= x && node[k].r <= y) {
        node[k].lazy += val;
        node[k].ma += val;
        return ;
    }
    push(k);
    int mid = (node[k].l + node[k].r) >> 1;
    if(x <= mid) change(ls);
    if(y > mid) change(rs);
    update(k);
}

void query(int k) {
    if(node[k].l >= x && node[k].r <= y) {
        ans = max(ans, node[k].ma);
        return ;
    }
    push(k);
    int mid = (node[k].l + node[k].r) >> 1;
    if(x <= mid) query(ls);
    if(y > mid) query(rs);
}

int main() {
    int t, kase = 0;
    scanf("%d", &t);
    while(t--) {
        scanf("%d%d", &n, &m);
        init();
        for(int i = 0; i < n - 1; i++) {
            int u, v;
            scanf("%d%d", &u, &v);
            add(u, v); add(v, u);
        }
        for(int i = 0; i < n; i++) 
            scanf("%lld", &sum[i]), num[i] = sum[i];
        dfs(0);
        build(0, n - 1, 1);
        printf("Case #%d:\n", ++kase);
        while(m--) {
            int type, a;
            scanf("%d%d", &type, &a);
            x = left[a]; y = right[a];
            if(type) {
                ans = -INF;
                query(1);
                printf("%lld\n", ans);
            }
            else {
                ll val1;
                scanf("%lld", &val1);
                val = val1 - num[a];
                change(1);
                num[a] = val1;
            }
        }
    }
    return 0;
}