机器学习---朴素贝叶斯模型

机器学习—朴素贝叶斯模型

1.通俗解释：

朴素贝叶斯模型的基本思路就是利用贝叶斯的后验概率公式来推算当前属性下的数据样本属于哪一个类别。直白一点说，就是在特征属性为当前取值的条件下，该样本归属于那个类别的可能性最大，就把该样本判断为那个类别。从这样的描述中可以看出，实际上我们关注的就是条件概率。而根据贝叶斯定理，条件概率实际上与“类别本身的概率”和“在该类别条件下特征属性为当前取值的条件概率”这两者的乘积成正比，由于特征属性维度较高，朴素贝叶斯通过假设属性条件成立，简化了计算。这就是朴素贝叶斯模型的基本思路。

换个表达形式就会明朗很多，如下：

2.任务类型：

朴素贝叶斯模型一般用于处理分类问题。朴素贝叶斯模型架设了特征属性之间的条件独立性，虽然现实中的数据都不一定能够满足该假设，但是即便不满足假设，模型在很多场景的结果也是可以接受的。

3.贝叶斯公式和全概率公式

贝叶斯与全概率
1 条件概率公式:
P(A|B)代表事件B发生的情况下A发生的概率。
P(A|B)=P(AB)/P(B)
2 全概率公式
A代表结果，B代表原因。导致A发生的原因B可以细化为B1、B2…Bn 。其中B1----Bn事件互斥，不可能同时出现。
P(A)=P(AB1)+P(AB2)+…+P(ABn)
=P(A|B1)P(B1)+P(A|B2)P(B2)+…+P(A|Bn)P(Bn)
每一个B都可能导致A的发生。
这是解决A在某些情况下不好求解的问题。
3 贝叶斯公式
与全概率公式正好相反，是求解事情发生的原因概率 P(Bi|A)
P(Bi|A)=P(Bi)P(A|Bi)/P(A)
P(A)可以按照2中的全概率公式展开

4.生成式模型和判别式模型

机器学习都可以被归为这两类。生成式模型：朴素贝叶斯，混合高斯模型，马尔科夫随机场等，而判别式模型：SVM，决策树，逻辑斯蒂回归，k邻近等，两种类型模型各有千秋。
生成式模型：可以在样本数量大时更好地学习到真实分布情况，并且能反应出更多的数据信息，但是要想对联合分布进行准确的估计，就需要大量的训练数据，这也是生成式模型的缺点。
判别式模型：直接面向目标（找到分类边界）因此准确性较好，需要的样本数也比生成式模型少，但是，判别式模型无法反映联合概率分布等信息。

5.代码实现

from  sklearn.naive_bayes import GaussianNB
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
#本实验应用葡萄酒分类数据集（Wine）首先加载数据集，并打印相关信息。
#加载wine数据集
wine=load_wine()
wine_data=wine.data
wine_target=wine.target
wine_target_names=wine.target_names
wine_feat_names=wine.feature_names
#打印相关信息
print('测试类别：',wine_target_names)
print('特征信息：',wine_feat_names)
print('信息描述：',wine.DESCR)
#划分训练集和测试集，常规操作
X_train,X_test,y_train,y_test=train_test_split(wine_data,wine_target,test_size=0.3,random_state=2021)
print('训练集与测试集数量与特征信息',X_train.shape,X_test.shape)
#输出训练集三种类别的数量
print(sum(y_train==0),sum(y_train==1),sum(y_train==2))
#建立朴素贝叶斯模型，并进行训练
print('无先验概率')
clt=GaussianNB()
clt.fit(X_train,y_train)
print(clt)
y_pred_train=clt.predict(X_train)
y_pred_test=clt.predict(X_test)
train_acc=sum(y_train==y_pred_train)/len(y_train)*1.0
test_acc=sum(y_test==y_pred_test)/len(y_test)*1.0
print("Train Accuracy is :{:.2f}".format(train_acc))
print("Test Accuracy is :{:.2f}".format(test_acc))
#这里的先验概率是三个类别分别在整个数据集中所占的比例
print('设置先验概率')
clt1=GaussianNB(priors=[59/178,71/178,48/178])
clt1.fit(X_train,y_train)
print(clt1)
y_pred_train=clt1.predict(X_train)
y_pred_test=clt1.predict(X_test)
train_acc=sum(y_train==y_pred_train)/len(y_train)*1.0
test_acc=sum(y_test==y_pred_test)/len(y_test)*1.0
print("Train Accuracy is :{:.2f}".format(train_acc))
print("Test Accuracy is :{:.2f}".format(test_acc))
 #在测试集上的混肴矩阵
print('测试集在混肴矩阵上的表示')
con_mat=confusion_matrix(y_test,y_pred_test)
print(con_mat)

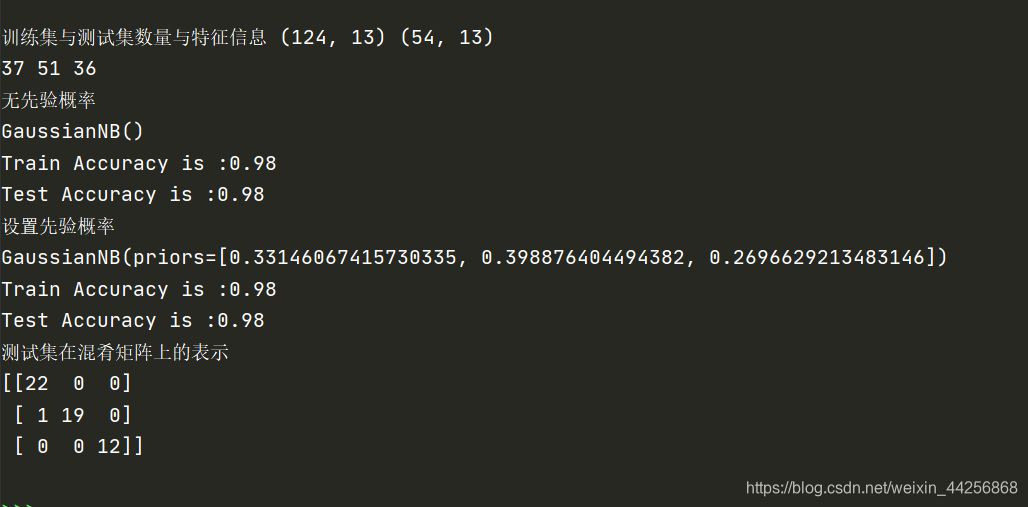
6.实验结果