机器学习-----曲面平铺：流形学习

机器学习-----曲面平铺：流形学习

1. 通俗解释：

流形学习是一种非线性降维的思路框架，利用流形学习原理的降维可以有不同的实现方法，例如Isomap(Isometric Mapping ,等距映射)和LLE（Locally Linear Embedding，局部线性嵌入）算法。流形学习的基本假设是，实际任务中的高维数据并不是在高维空间散乱分布的，而是分布在某个流形上。流形可以直观地被想象成高维空间中的一个曲面，流形学习就是将这样的曲面展平在较低维的空间，并保持数据点之间的距离和结构关系尽量不变。

2. 任务类型:

流形学习可以被用在很多非线性降维的任务，另外，如果降维到二维或三维，可以实现数据的可视化。由于流形学习可以保持样本之间的距离和结构关系尽量不变，因此可以帮助我们在二维或三维空间中直观地看到数据样本点之间的关系。

3. Isomap算法步骤

Isomap算法是基于样本之间的距离关系，利用图论方法计算样本之间的测地距离，并转换为低维坐标的流形学习的降维方法。基本步骤如下;

1. 通过k近邻找到局部欧氏空间近似，直接用欧氏距离计算出相邻样本间的距离。
2. 利用图论中的带权平均值进行建模。将样本看作图中的顶点，k邻域中的已经直接计算出距离的点由边连接，边的权重就是两点之间的距离。
3. 利用Floyd算法，更新所有样本点之间的最短路径，得到的结果即任意两点间的测地距离。
4. 利用MDS并结合特征值的个数选取，将距离转换成坐标的同时并降维。降维后的结果的样本间距离与原始数据在流形上的测地距离接近，从而实现了分布在流形上的数据降维。

4.LLE算法基本思路

LLE算法主要关注样本与近邻的局部结构。基本步骤如下：

1. 对每个样本数据，确定其近邻点。
2. 将线性表示系数作为优化变量，通过求解优化问题得到每个样本的局部线性表示。
3. 利用得到的局部线性表示系数矩阵，求解低维空间中重构的优化问题，从而保证降维后局部结构基本不变。具体实现时可以通过特征值分解的方法确定降维后的数据表示。

5.代码实现

from sklearn.datasets import make_swiss_roll
from sklearn.manifold import LocallyLinearEmbedding,Isomap
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
#利用生成器生成Swiss Roll数据集，共3000样本点
X,t=make_swiss_roll(n_samples=3000,noise=0.1,random_state=2021)
#作图显示Swiss Roll在三维空间中的分布
fig=plt.figure(figsize=(8,8))
ax=fig.add_subplot(111,projection='3d')
ax.scatter(X[:,0],X[:,1],X[:,2],c=t,cmap=plt.cm.jet)
ax.view_init(10,60)
ax.set_xlabel('x axis',fontdict={'family':'Times New Roman','size':20})
ax.set_ylabel('y axis',fontdict={'family':'Times New Roman','size':20})
ax.set_zlabel('z axis',fontdict={'family':'Times New Roman','size':20})
ax.set_title('Swiss Roll ',fontdict={'family':'Times New Roman','size':20})
fig.show()
#利用Isomap算法将原始数据降至二维，在计算邻域点时，认为最近的20个邻域点为直接可达
islomap_model=Isomap(n_components=2,n_neighbors=20)
islomap_model.fit(X)
X_islomap_reduce=islomap_model.fit_transform(X)
#作图显示降维后的结果
fig1=plt.figure(figsize=(8,4))
ax2=fig1.add_subplot(111)
ax2.scatter(X_islomap_reduce[:,0],X_islomap_reduce[:,1],c=t,cmap=plt.cm.jet)
ax2.set_xlabel('x axis',fontdict={'family':'Times New Roman','size':20})
ax2.set_ylabel('y axis',fontdict={'family':'Times New Roman','size':20})
ax2.set_title('Isomap result',fontdict={'family':'Times New Roman','size':40})
fig1.show()
#利用LLE算法将原始数据降至二维，在计算邻域结构时，认为最近的20个邻域点为直接可达
lle_model=LocallyLinearEmbedding(n_neighbors=20,n_components=2)
lle_model.fit(X)
X_lle_reduce=lle_model.fit_transform(X)
#作图显示降维后的结果
fig2=plt.figure(figsize=(8,4))
ax3=fig2.add_subplot(111)
print(X_lle_reduce[:,0],X_lle_reduce[:,1])
ax3.scatter(X_lle_reduce[:,0],X_lle_reduce[:,1],c=t,cmap=plt.cm.jet)
ax3.set_xlabel('x axis',fontdict={'family':'Times New Roman','size':20})
ax3.set_ylabel('y axis',fontdict={'family':'Times New Roman','size':20})
ax3.set_title('LLE result',fontdict={'family':'Times New Roman','size':40})
fig2.show()

6.实验结果

原始数据分布：

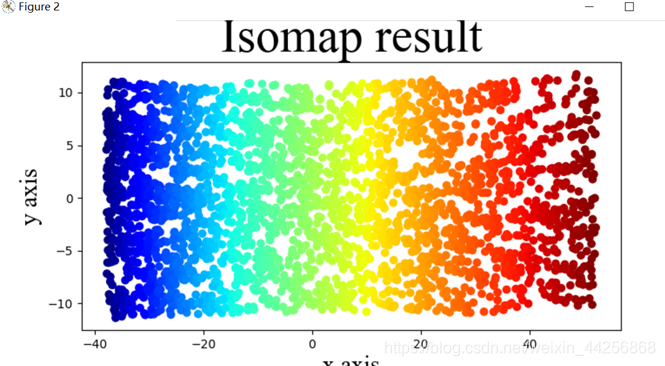
Isomap算法实现结果：

LLE算法实现结果：