欧拉角表示的姿态矩阵（313和312转序）

原创已于 2023-04-18 21:31:21 修改 · 6.5k 阅读

34 ·

CC 4.0 BY-SA版权

文章标签：

#矩阵

于 2022-08-17 21:06:04 首次发布

天文专栏收录该内容

2 篇文章

订阅专栏

本文介绍了基本旋转矩阵在惯性导航系统（PSINS）中的应用，包括绕x、y、z轴的逆时针旋转，并详细解析了313(ZXZ)和312(ZXY)转序方法，以及如何通过C矩阵计算姿态角。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、习惯约定

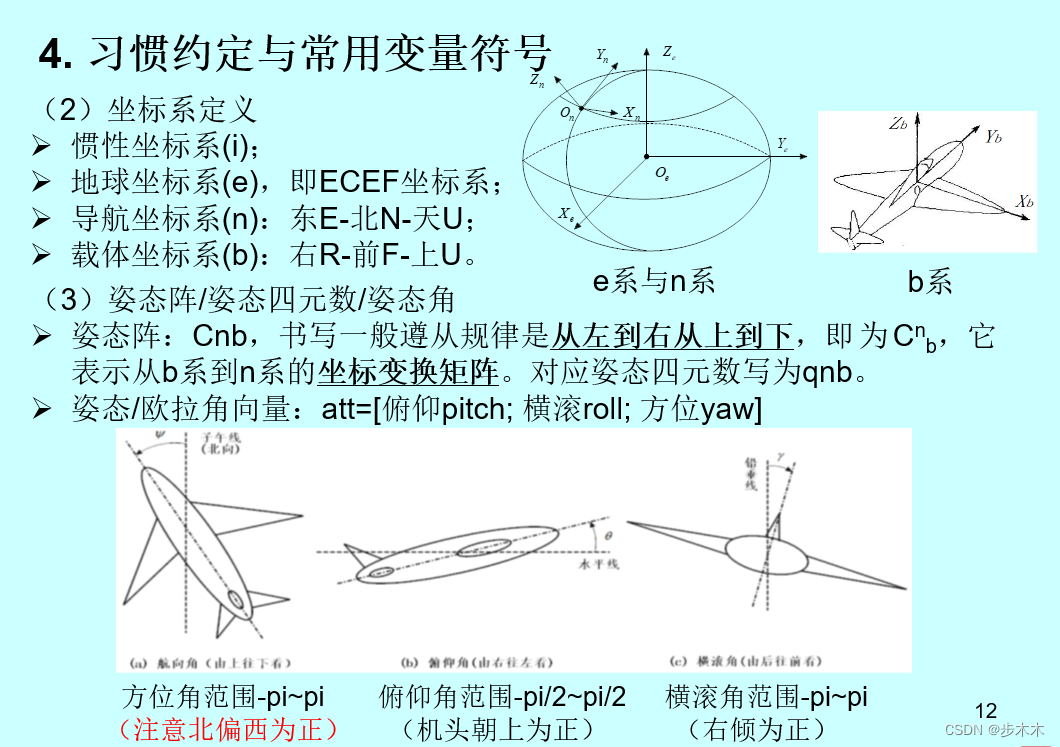
在这里插入图片描述
图片来自 PSINS（高精度捷联惯导算法） PSINS工具箱入门与详解.pptx

二、基本旋转矩阵

绕x轴逆时钟旋转 $\alpha$ 角度
$R_x(\alpha)=\begin{bmatrix} \ 1 & 0 & 0 \\ 0 & \cos \alpha & \sin \alpha \\ 0 & -\sin \alpha & \cos \alpha\end{bmatrix}$
绕y轴逆时钟旋转 $\alpha$ 角度
$R_y(\alpha)=\begin{bmatrix} \ \cos \alpha & 0 & -\sin \alpha \\ 0 & 1 & 0 \\ \sin \alpha & 0 & \cos \alpha\end{bmatrix}$
绕z轴逆时钟旋转 $\alpha$ 角度
$R_z(\alpha)=\begin{bmatrix} \cos \alpha & \sin \alpha & 0 \\ -\sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{bmatrix}$

三、313转序（ZXZ）

在这里插入图片描述

ZXZ转序如图所示，转角依次为： $\psi$ 、 $\theta$ 、 $\phi$ ，即绕 $z$ 轴转 $\psi$ 角，在绕 $x^{'}$ 轴转 $\theta$ 角，最后绕 $z^{''}$ 轴转 $\phi$ 角。

根据基本旋转矩阵，可得出姿态矩阵
$\begin{align} C &= R_z(\phi)R_x(\theta)R_z(\psi)\\ &= \begin{bmatrix} \cos \phi & \sin \phi & 0 \\ -\sin \phi & \cos \phi & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} \ 1 & 0 & 0 \\ 0 & \cos \theta & \sin \theta \\ 0 & -\sin \theta & \cos \theta\end{bmatrix} \begin{bmatrix} \cos \psi & \sin \psi & 0 \\ -\sin \psi & \cos \psi & 0 \\ 0 & 0 & 1 \end{bmatrix}\\ &= \begin{bmatrix} \cos\phi\cos\psi-\sin\phi\cos\theta\sin\psi & \cos\phi\sin\psi+\sin\phi\cos\theta\cos\psi & \sin\phi\sin\theta \\ -\sin\phi\cos\psi-\cos\phi\cos\theta\sin\psi & -\sin\phi\sin\psi+\cos\phi\cos\theta\cos\psi & \cos\phi\sin\theta \\ \sin\theta\sin\psi & -\sin\theta\cos\psi & \cos\theta \end{bmatrix} \end{align}$
$\begin{equation} \left\{ \begin{array}{lr} \psi=-\arctan\dfrac{C_{zx}}{C_{zy}} \\ \theta=\arccos{C_{zz}}\\ \phi=\arctan\dfrac{C_{xz}}{C_{yz}} \end{array} \right. \end{equation}$

四、312转序（ZXY）

在这里插入图片描述
ZXY转序如图所示，转角依次为： $\psi$ 、 $\phi$ 、 $\theta$ ，即绕 $z$ 轴转 $\psi$ 角，在绕 $x^{'}$ 轴转 $\phi$ 角，最后绕 $y^{''}$ 轴转 $\theta$ 角。

根据基本旋转矩阵，可得出姿态矩阵
$\begin{align} C &= R_y(\theta)R_x(\phi)R_z(\psi)\\ &=\begin{bmatrix} \ \cos \theta & 0 & -\sin \theta \\ 0 & 1 & 0 \\ \sin \theta & 0 & \cos \theta\end{bmatrix}\begin{bmatrix} \ 1 & 0 & 0 \\ 0 & \cos \phi & \sin \phi \\ 0 & -\sin \phi & \cos \phi\end{bmatrix} \begin{bmatrix} \cos \psi & \sin \psi & 0 \\ -\sin \psi & \cos \psi & 0 \\ 0 & 0 & 1 \end{bmatrix}\\ &= \begin{bmatrix} \cos\theta\cos\psi-\sin\theta\sin\phi\sin\psi & \cos\theta\sin\psi+\sin\theta\sin\phi\cos\psi & -\sin\theta\cos\phi \\ -\cos\phi\sin\psi & \cos\phi\cos\psi & \sin\phi \\ \sin\theta\cos\psi+\cos\theta\sin\phi\sin\psi & \sin\theta\sin\psi-\cos\theta\sin\phi\cos\psi & \cos\theta\cos\phi \end{bmatrix} \end{align}$
$\begin{equation} \left\{ \begin{array}{lr} \psi=-\arctan\dfrac{C_{yx}}{C_{yy}} \\ \theta=\arcsin{C_{yz}}\\ \phi=-\arctan\dfrac{C_{xz}}{C_{zz}} \end{array} \right. \end{equation}$