Floquet理论详解：周期线性系统的稳定性分析

Floquet理论详解：周期线性系统的稳定性分析

一、引言

在实际工程系统中，如电力电子控制系统、振动系统或通信调制系统，常常会遇到系数周期变化的线性系统。这些系统不能用常系数微分方程的传统方法进行稳定性分析。为此，Floquet理论应运而生。

Floquet理论是一种用于研究**线性周期时变系统（Linear Periodic Time-Varying Systems）**稳定性的重要数学工具。它提供了一种将周期微分方程转换为指数形式加周期函数的分解方法，极大地简化了系统分析

二、系统模型与基本解矩阵

我们考虑一个n维线性周期微分系统，其状态方程为：

$$\dot{x}(t)=A(t)x(t)\text{\hspace{1em}(1)}$$

其中：

• $x(t)\in {\mathbb{R}}^n$：系统状态向量；
• $A(t)\in {\mathbb{R}}^{n\times n}$：周期为 $T$ 的连续矩阵函数，即 $A(t+T)=A(t)$。

系统的解结构可通过构造基本解矩阵（Fundamental Matrix）来研究。

基本解矩阵定义：

矩阵函数 $\Phi (t)\in {\mathbb{R}}^{n\times n}$ 被称为系统（1）的基本解矩阵，若满足：

$$\frac{d}{dt}\Phi (t)=A(t)\Phi (t),\Phi (0)=I\text{\hspace{1em}(2)}$$

其中 $I$ 为单位矩阵。该矩阵的每一列构成系统的线性无关解，因此任意初值 $x(0)$ 的解可写为：

$$x(t)=\Phi (t)x(0)\text{\hspace{1em}(3)}$$

三、Floquet定理及其结构分解

Floquet定理指出：对于周期线性系统（1），其基本解矩阵 $\Phi (t)$ 可表示为：

$$\Phi (t)=P(t)e^{Rt}\text{\hspace{1em}(4)}$$

其中：

• $P(t)$ 是周期为 $T$ 的可逆矩阵函数，即 $P(t+T)=P(t)$；
• $R\in {\mathbb{C}}^{n\times n}$ 是常系数矩阵（可能是复数）。

推导简要说明：

将式(4)代入(2)中，有：

$$\dot{\Phi }(t)=\dot{P}(t)e^{Rt}+P(t)R{e}^{Rt}=A(t)P(t)e^{Rt}\Rightarrow \dot{P}(t)+P(t)R=A(t)P(t)\text{\hspace{1em}(5)}$$

这表明 $P(t)$ 应满足一个类似李雅普诺夫方程的非齐次微分关系，其周期性构造与常系数矩阵 $R$ 的引入相辅相成。

四、单周期矩阵与Floquet乘子

单周期矩阵定义：

令基本解矩阵在 $t=T$ 时为：

$$\Phi (T)=P(0)e^{RT}\text{\hspace{1em}(6)}$$

定义该矩阵为系统的单周期矩阵（Monodromy Matrix）：

$$M:=\Phi (T)\text{\hspace{1em}(7)}$$

该矩阵描述了系统一个周期内从状态 $x(0)$ 到 $x(T)$ 的映射关系。

Floquet乘子与Floquet指数：

设 ${\rho }_i$ 为 $M$ 的特征值，即：

$$M{v}_i={\rho }_i{v}_i\text{\hspace{1em}(8)}$$

称 ${\rho }_i$ 为Floquet乘子。设 ${\lambda }_i$ 为常系数矩阵 $R$ 的特征值，满足：

$${\rho }_i=e^{{\lambda }_{i}T},{\lambda }_i=\frac{1}{T}\ln {\rho }_i\text{\hspace{1em}(9)}$$

称 ${\lambda }_i$ 为Floquet指数。它揭示了解中指数增长或衰减的速率。

五、稳定性分析准则

系统的稳定性可通过Floquet乘子判断：

• 若所有Floquet乘子的模均小于1，即 $|{\rho }_i|<1$，系统渐近稳定；
• 若存在某个乘子满足 $|{\rho }_i|>1$，系统不稳定；
• 若所有 $|{\rho }_i|\le 1$，但存在模等于1的重根，需进一步判断系统是否临界稳定。

从物理角度来看：

• $|{\rho }_i|<1$：扰动随周期衰减；
• $|{\rho }_i|=1$：扰动维持不变（振荡）；
• $|{\rho }_i|>1$：扰动放大，导致不稳定。

六、Floquet理论应用流程

在工程实际中，使用Floquet理论进行稳定性分析的一般步骤如下：

1. 建立系统状态空间方程 $\dot{x}(t)=A(t)x(t)$，确认 $A(t)$ 为周期函数；
2. 计算一个周期的基本解矩阵 $\Phi (T)$，通常通过数值积分实现；
3. 构造单周期矩阵 $M=\Phi (T)$，并求其特征值；
4. 判断Floquet乘子的模，据此确定系统稳定性。

如图所示（见你提供的图3-1流程图），Floquet理论可嵌入VSG系统稳定性分析流程中，作为周期控制系统时域稳定性的判据。

七、示例与简要说明（复杂情形）

▶ 假设某系统的单周期矩阵为：

$$M=\left[\begin{array}{cc}0.7& -0.6\\ 0.6& 0.7\end{array}\right]$$

▶ 第一步：求 Floquet 乘子（即矩阵特征值）

特征方程为：

$$\det (M-\rho I)=0\Rightarrow \left|\begin{array}{cc}0.7-\rho & -0.6\\ 0.6& 0.7-\rho \end{array}\right|=0$$

$$(0.7-\rho {)}^2+0.6^2=0\Rightarrow (0.7-\rho {)}^2=-0.36\Rightarrow \rho -0.7=\pm j0.6\Rightarrow \rho =0.7\pm j0.6$$

▶ 第二步：分析 Floquet 乘子模长

$$|\rho |=\sqrt{0.7^2+0.6^2}=\sqrt{0.49+0.36}=\sqrt{0.85}\approx 0.922$$

▶ 第三步：稳定性分析

• 两个乘子是共轭复数对，表示系统存在周期性的振荡行为；
• 但乘子模长 $<1$，说明振荡是收敛的；
• 结论：系统是渐近稳定的，同时具有振荡衰减特性。

✅ 工程含义说明：

• 这种情形非常常见于含有电感/电容回路或控制器滞后环节的电力系统或VSG中；
• 振荡的频率取决于乘子的虚部（$j0.6$ 对应角频率 $\omega =\frac{\arg (\rho )}{T}$）；
• 稳定性取决于模值 $|\rho |<1$，即每周期状态“缩小”程度。

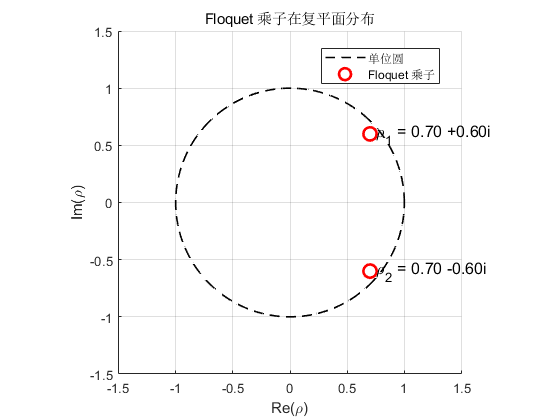
✅ 可视化辅助理解：

如果画在复平面中，这两个 Floquet 乘子分别位于单位圆内，形成一对对称点，轨迹绕原点旋转并收敛。

✅ 总结这个例子：

项目	值
单周期矩阵 $M$	$\left[\begin{array}{cc}0.7& -0.6\\ 0.6& 0.7\end{array}\right]$
Floquet 乘子	$0.7\pm j0.6$
模值	$\approx 0.922<1$
系统状态行为	振荡收敛、渐近稳定

八、总结

项目	含义
$\dot{x}(t)=A(t)x(t)$	周期线性微分系统
$\Phi (t)=P(t)e^{Rt}$	Floquet解结构分解
$\Phi (T)$	单周期矩阵（Monodromy矩阵）
${\rho }_i$	Floquet乘子：$\Phi (T)$ 的特征值
${\lambda }_i$	Floquet指数：${\lambda }_i=\ln ({\rho }_i)/T$
稳定性条件	所有 |${\rho }_i$| < 1 则系统稳定

Floquet理论将时变系统的分析“简化”为常系数系统的特征值问题，极大地扩展了我们分析周期控制系统稳定性的能力。它不仅具有理论价值，更在现代电力电子、电机控制、通信与导航系统中有广泛应用。

九、MATLAB分析代码

% Floquet Visualization in Complex Plane

clc; clear;

% -----------------------------
% 1. 定义单周期矩阵 M
M = [0.7, -0.6;
     0.6,  0.7];

% -----------------------------
% 2. 计算 Floquet 乘子（特征值）
rho = eig(M);

% -----------------------------
% 3. 绘制单位圆与 Floquet 乘子

theta = linspace(0, 2*pi, 500);
unit_circle = exp(1j*theta);

figure;
hold on; grid on; axis equal;

% 绘制单位圆
plot(real(unit_circle), imag(unit_circle), 'k--', 'LineWidth', 1.2);

% 绘制 Floquet 乘子
plot(real(rho), imag(rho), 'ro', 'MarkerSize', 10, 'LineWidth', 2);

% 设置坐标轴
xlim([-1.5, 1.5]);
ylim([-1.5, 1.5]);
xlabel('Re(\rho)');
ylabel('Im(\rho)');
title('Floquet 乘子在复平面分布');

% 标注每个乘子的数值
for i = 1:length(rho)
    text(real(rho(i)) + 0.05, imag(rho(i)), ...
        sprintf('\\rho_{%d} = %.2f %+.2fi', i, real(rho(i)), imag(rho(i))), ...
        'FontSize', 12);
end

legend('单位圆', 'Floquet 乘子', 'Location', 'best');