回溯算法 + 剪枝专题

       回溯算法，相比大家再熟悉不过了，全排列、八皇后、迷宫问题、人狼羊菜过河、人鬼渡河等问题都可用回溯算法解决，但我们如何解决这类问题呢?
       回溯实质上也是枚举，即可尝试所有情况，我们来看一张图:

       画的不是很标准，但勉强能看，这是一棵满 n 叉树，可以借用此模型来理解回溯算法，即层层深入，直到叶子节点(底层)才返回，返回上一父节点，继续进入下一节点，直至遍历完整棵满 n 叉树。
       代码架构如下:

#include <iostream>
#include <algorithm>
using namespace std;

int n, x[1024], cnt = 0;//x[]存放排列内容 

void OutPut()
{
	printf("%d :", ++cnt);
	for(int i = 1; i <= n; ++i) printf("%d ", x[i]);
	putchar('\n');
}

void Full_Permutation(int k)
{
	if(k > n) OutPut();
	else
	{
		for(int i = 1; i <= n; ++i)
		{
			x[k] = i; 
			Full_Permutation(k + 1);	
		} 
	}
}

int main()
{
	scanf("%d", &n);
	Full_Permutation(1);
	return 0;
}

       这是最简单也是最初的回溯模型，即无任何条件限制(没有剪枝)，但如果我们要输出全排列，即每个数字均不相同，这时需要进行剪枝，即在for循环下卡住对应的条件即每位数字不相等，与前面的数字一一比较即可。
       全排列(未优化)

void OutPut()
{
	printf("%d :", ++cnt);
	for(int i = 1; i <= n; ++i) printf("%d ", x[i]);
	putchar('\n');
}

//
if(Prune(k, i))//剪枝 
{
	x[k] = i; 
	Full_Permutation(k + 1);	
} 

       关键点来了，这我需要每次都与前面记录的数相比较，付出了$O(n)$级别的代价，那我能否在一开始采用一个一维数组记录它是否被纳入x[]数组中呢?
       答案当然可以

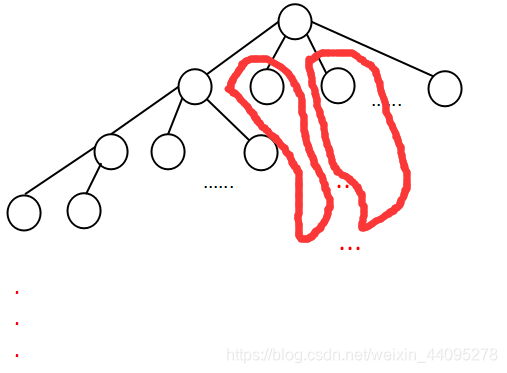
       我们来看一下我所框住的这两棵子树，注意你的标记数组为全局共享并不是那一颗子树所专有的，所以当你遍历完一棵子树时，理应释放，以供另另一个子树继续使用，否则全部都标记为1时(已占用)，按理如就只能得到一个值，因为已标记为1其它子树无法使用
       优化如下:

		if(Prune(i))//剪枝, 该数字是否被用 
		{
			x[k] = i;
			book[i] = 1; 
			Full_Permutation(k + 1);
			book[i] = 0;//全局数组共享，置 0 以便满n叉树的其它子树使用	
		}

       if()条件语句内即为剪枝，卡一个条件，它能否继续深入即是否满足我所设置的条件，我可以再举几个例子

纯净串、暗黑串:
#include <iostream>
#include <algorithm>
using namespace std;

int n, cnt = 0;
char x[1024]; 
//只限于A, B, C三类 
int Prune(int k, int i)
{
	if(k > 2 && x[k - 2] != x[k - 1] && x[k - 1] != i + 'A' && x[k - 2] != i + 'A') return 0;
	else
	{
		return 1;	
	} 
}

void OutPut()
{
	printf("%d :", ++cnt);
	for(int i = 1; i <= n; ++i) printf("%c", x[i]);
	putchar('\n');
}

void Full_Permutation(int k)
{
	if(k > n) OutPut();
	else
	{
		for(int i = 0; i <= 2; ++i)//A, B, C 
		if(Prune(k, i))//剪枝 
		{
			x[k] = i + 'A'; 
			Full_Permutation(k + 1);	
		} 
	}
}

int main()
{
	scanf("%d", &n);
	Full_Permutation(1);
	return 0;
}

八皇后问题:
#include <iostream>
#include <algorithm>
using namespace std;

int n, x[1024] = {0}, cnt = 0;
int a[1024] = {0}, b[1024] = {0}, c[1024] = {0}; 
//  优化方案 
int Prune(int k, int i)
{
	if(a[i] || b[k + i] || c[k - i + n]) return 0;
	else
	{
		return 1;
	}
}

void OutPut()
{
	printf("%d\n", ++cnt);
	for(int i = 1; i <= n; ++i)
	{
		for(int j = 1; j < x[i]; ++j)      printf("* ");
		printf("Q ");
		for(int j = x[i] + 1; j <= n; ++j) printf("* ");
		putchar('\n');
	}
	putchar('\n');
}

void Eight_queens(int k)
{
	if(k > n) OutPut();
	else
	{
		for(int i = 1; i <= n; ++i)
		if(Prune(k, i))//剪枝 
		{
			x[k] = i;
			a[i] = b[k + i] = c[k - i + n] = 1; 
			Eight_queens(k + 1);
			a[i] = b[k + i] = c[k - i + n] = 0; 
		} 
	}
}

int main()
{
	scanf("%d", &n);
	Eight_queens(1);
	return 0;
}

       最后来一个重头戏，走迷宫问题，我要求所给迷宫的从左上角 -> 右下角 的全部路径，同样也可以用回溯法解决，它只有四个方向，上、下、左、右，此时为满 4 叉树，在剪枝时注意:
       1.它不是墙壁
       2.它没有走过
       3.它没有出界
       在回溯处理时，回退的不仅路径，还有标记是否走过、和记录的坐标点，在到达右下角输出即可
       废话不多说，上代码:

#include <iostream>
#include <algorithm>
#include <cmath>
//给定一个r x c大小的矩阵, #代表墙, . 代表路, 求其最短路径 
int r, c;//矩阵大小
int num1[101], num2[101], total = 0;//存储数据
int wayr[4] = {0, 0, 1, -1}, wayc[4] = {1, -1, 0, 0};//进行移动
bool mark[101][101];//路径标记 
char maze[101][101];//迷宫 
bool check(int x, int y)//判断是否出局 
{
	if(x <= 0 || y <= 0 || x > r || y > c) return false;
	return true;
}

void println()//输出函数 
{
	printf("(1,1)");
	for(int i = 1; i <= total; ++i)
	{
		printf("->(%d, %d)", num1[i], num2[i]);	
	}
	putchar('\n');	
} 

void search(int x, int y)//搜索函数，用于遍历迷宫 
{
//	回溯
	for(int i = 0; i < 4; ++i)//i = 0、1、2、3 下、上、右、左四个方向
	{
		if(!mark[x + wayr[i]][y + wayc[i]] && check(x + wayr[i], y + wayc[i]) && maze[x + wayr[i]][y + wayc[i]] == '.')//判断是否走过、为墙、超过边界 
		{
			x += wayr[i];//行变换 
			y += wayc[i];//列变换
			++total;
			num1[total] = x;   //记录行号 
			num2[total] = y;   //记录列号 
			if(x == r && y == c) println();//已到右下角
			mark[x][y] = true; 
			search(x, y); 
			mark[x][y] = false;//回溯 
			--total;//行列号的记录回退
			x -= wayr[i];//行 回退 
			y -= wayc[i];//列 回退	
		}	
	} 
}

int main()
{
	scanf("%d %d", &r, &c);
	for(int i = 1; i <= r; ++i)
	for(int j = 1; j <= c; ++j)
	{
		if(j == 1)  scanf(" ");
		scanf("%c", &maze[i][j]);	
	}
	mark[1][1] = true;//标记起点，已走过 
	search(1, 1);
	return 0;	
} 
/*
5 4
.###
...#
##.#
#...
#...
*/

       当如果求其最短路径，则一次比较所得到的路径，找出最短的一个路径即可，这也是回溯算法的一个典型应用。