机器学习 - 基础算法 - 决策树

决策树算法概述

    决策树（decision tree）决策树属于解释性比较强的分类算法，可以理解我们要处理的数据就是树的根节点，数据的特征被看作每一个节点，每次决策会在特征节点产生新的分支并反复。这种迭代决策的方式有点像一套if else语句递归判断。

    选择礼物是否会喜欢，有几个属性：颜色、价格、大小。

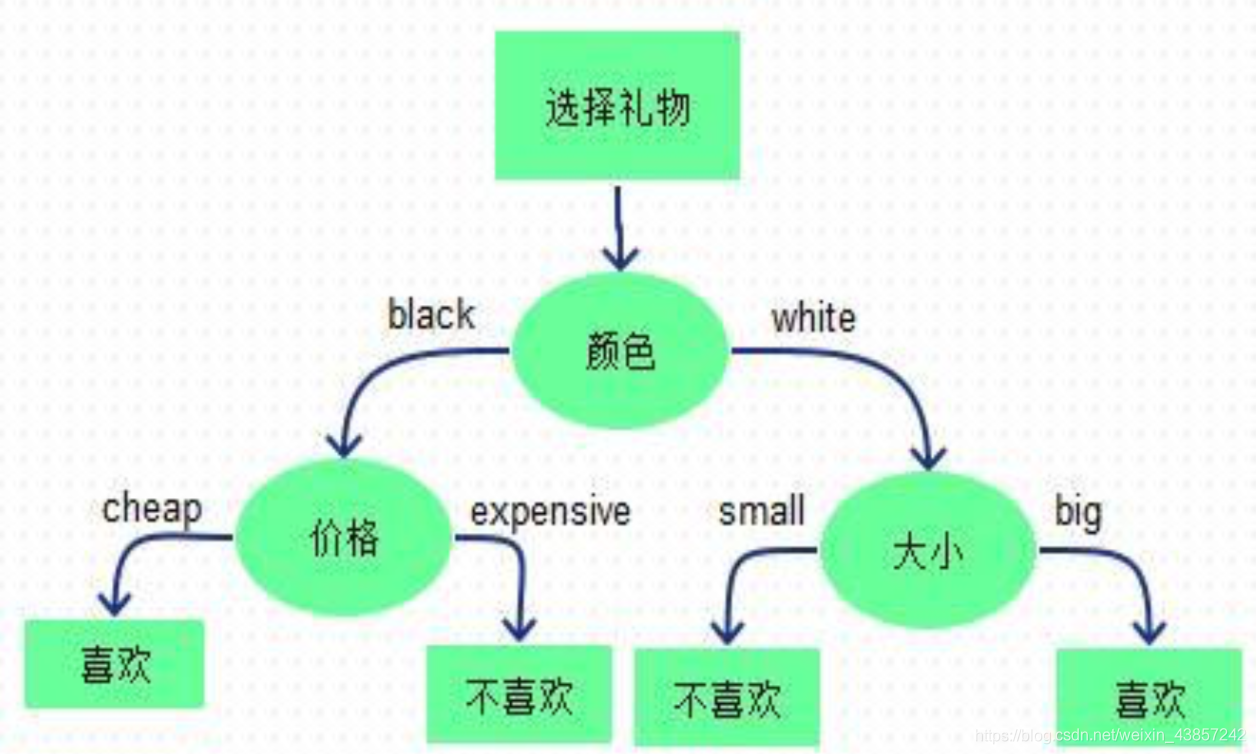
决策树流程

    训练模型救相当于就是在构建一个树，递归寻找衡量每个数据集划分特征的最优分类，如果一个数据集合中只有一种分类结果，则该集合最纯，即一致性好。

• 开始阶段（节点选择）
  从根结点(root node)开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征。

• 迭代阶段（决策树生成）
  由该特征的不同取值建立子节点，再对子结点递归地调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为止

• 完成阶段（决策树修剪）
  剪枝得到一个完整的决策树

节点特征选择

    节点的选择也就是特征的选择，必须是纯度高的这样对数据才会有良好的划分，一般评估信息纯度有几种算法：

ID3（信息增益）

ID3使用最大信息熵增益（Information Gain）来选择分割数据的特征。

• 信息增益 = 分类前的信息熵 - 分类后的信息熵
• 信息熵：熵在信息论中代表随机变量不确定度的度量，通过样本集合的不确定性度量样本集合的纯度，表示不确定度，均匀分布时，不确定度最大，此时熵就最大，分类后熵小。
• 熵越大，数据的不确定性越高
• 熵越小，数据的不确定性越低

信息增益：可以衡量某个特征对分类结果的影响大小，越大越好。

中X 表示的是随机变量，随机变量的取值为(x1,x2,…,xn) ，p({x_i}) 表示事件xi发生的概率，且有∑p(xi)=1 。信息熵的单位为bit。
举例来说，假设3个事件的发生概率分别是
$$\frac{1}{10}、\frac{2}{10}、\frac{7}{10}$$
那么他的信息熵根据公式可以得到H = 0.8018
$$H=-\frac{1}{10}log(\frac{1}{10})-\frac{2}{10}log(\frac{2}{10})-\frac{7}{10}log(\frac{7}{10})=0.8018$$

CART（GINI系数）

GINI系数随机从D中抽取两个样本，其类别标记不一致的概率作为纯度的判定，不一致的概率越大，纯度越低。

• 基尼系数越高，不确定性越高
• 基尼系数越低，不确定性越低

举例来说三个事件的发生概率分别为
$$\frac{1}{10}、\frac{2}{10}、\frac{7}{10}$$
那么GINI系数为G = 0.46
$$1-(\frac{1}{10}{)}^2-(\frac{2}{10}{)}^2-(\frac{7}{10}{)}^2=0.46$$

C4.5（信息增益比）

    在ID3算法的基础上，进行算法优化提出的一种算法(C4.5)；现在C4.5已经是特别经典的一种决策树构造算法；使用信息增益率来取代ID3算法中的信息增益，在树的构造过程中会进行剪枝操作进行优化；能够自动完成对连续属性的离散化处理；C4.5算法在选中分割属性的时候选择信息增益率最大的属性

决策树优缺点

• 优点
  • 计算复杂度不高，输出结果具有较好的可解释性。
  • 对中间值的缺失不敏感，可以处理不相关特征数据，
  • 可以解决多分类问题
• 缺点
  • 可能会产生过度匹配的问题（过拟合问题）

决策树算法模型的实际应用

#!/usr/bin/python
# -*- coding: utf-8 -*-

from sklearn import tree
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

"""
从sklearn自带的数据集读取数据
"""


def load_data():
    iris = load_iris()
    return iris


"""
使用决策树，设置超参数max_depth=5训练，并测试准确度
"""


def DTC():
    clf = tree.DecisionTreeClassifier(max_depth=5)
    clf.fit(x_train, y_train)
    print("准确度:", clf.score(x_test, y_test))


"""
画图，x,y是所需要的数据
"""

def plt_show(x, y):
    plt.scatter(x[:, 2], x[:, 3], c=y)
    plt.show()


x_train, x_test, y_train, y_test = train_test_split(load_data().data, load_data().target, test_size=0.3,
                                                    random_state=1)

DTC()
plt_show(x_test, y_test)

参考文献

• 机器学习 - 周志华 清华大学出版社

最后

    本人工作原因文章更新不及时或有错误可以私信我，另外有安全行业在尝试做机器学习+web安全的小伙伴可以一起交流