“不胜之胜”之分析

“不胜之胜”之分析

（一）面对“上帝”与“恶魔”的决策
在一个假设的场景下：一个行人在路上幸运地碰到了上帝，上帝给了他两个选择：第一，什么事情都不做，直接馈赠给他250元；第二，掷骰子，赌大小。如果他赢了，得到550元；反之，如果他赢了，他得倒贴50元。

这个行人继续走，却碰到了海怪。这位行人原来有1000元，但之前却不小心丢掉了50元，现在口袋里还有950元。这个海怪很仗义，还是给了他两个选择：第一，什么事情也不做，给海怪400元，让海怪放他过去；第二，掷骰子，赌大小。如果他赢了，海怪给他100元；反之，如果他输了，他就得交出900元。

这个行人将会怎么选？

如果从概率论的角度来讲，对于上帝给出的选择其期望值都是相同的，均为获得250元。对于海怪的选择也是相同，期望值均为失去400元。然而由于心理因素的干扰，比起得到更不愿意失去，行人的选择会具有倾向性。对于大部分人而言，在第一个场景里总是更倾向于选择第一种方案，而在第二个场景里面总是希望选择第二种方案。

（二）不胜之胜的胜利

在天行九歌第49集里，韩非邀请李斯人同玩一个游戏，两人各有一枚金币。两人同时展示手中硬币的正反，若硬币正反相同，则李斯（A）得金叶子（分数）；正反相异，则韩非（B）得金叶子（分数）。若同为正则李斯（A）得3片金叶子（分），若同为反则李斯（A）得1片金叶子（分），相异则韩非（B）得2片金叶子（分）。

现在分为四种情况来讨论这个问题：

情况一：AB均无决策偏好

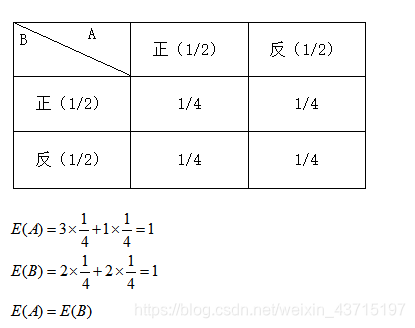
然而实际上A的决策偏好，更可能会输掉这场游戏。

相比较而言，对B而言出正反的权重相同，所以他出正反的几率是相同的；对A而言，正反却具有不同的权重，假设在花色相同的情况下，出正得到的分数更大，得到的收益更大。

情况二：所以A会在游戏中出现更多的出正的倾向，而打破了实际上的等概率的胜负。若假设A出正的概率上升为2/3，反为1/3；B正反的概率均为1/2。

情况三：如果B预料到A的这种倾向，也提高自己出反的几率，假设B调整自己出正的几率为1/3，反为2/3。

所以当A一旦有了想要以某种偏好来增大收益的倾向的时候，同样为理性决策人的B会调整自己的战略，而使得A失败的风险增高。

情况四：若B以为A会提高风险，而A实际上没有采取任何策略。A出正反的概率都为1/2，B出正的概率为1/3，反的概率为2/3。

当B选择增大出反的几率的策略后，增加了自己获胜的几率。

情况五：如果A已经预测到B的策略，通过增加自己出反的几率来应对。AB出正的概率均为1/3，反的概率为2/3。

对A而言还是输。

所以事实上在这个游戏里掌握主动权的始终是B。当把B采取了增加自己出反几率的策略后，A就已经处于劣势。

而如果B并没有意识到自己应该采取策略，A不采取策略的时候，这个游戏才能算得上公平。
对A而言，采取让自己增大出正的几率实际上是一种陷阱。尤其是在B深谙这个游戏精髓的情况下。
但基于第一个故事我们可以料想到，对于大部分人而言，都会犯这样的错误：在稳定的环境中，决策者不会选择风险大的决策；而在危机或者复杂性环境中，决策者则会像赌徒一般选择冒险的方式尽可能地去弥补可能失去的成本。A只要有一点分数上的落后，就必然会基于这种心理倾向而使用策略，掉入陷阱。

以上是理论分析，作为开着上帝视角，拿着放大镜看动漫的人，暂停统计了两局游戏里韩非和李斯的出硬币套路，列表如下：

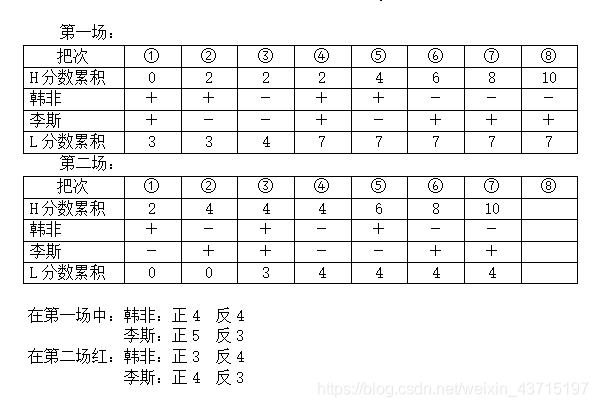
在第一场中有一个节点，第5把之后，李斯显然落后，为了追回得分，他会更加甘愿冒险，所以在最后一把中，求胜心切反而输了。
在第二场中暂且假设韩非采用了策略，李斯输得太快，第七把过后，胜负已见分晓。

韩非说，取胜的关键在于利用对手的贪念，对于李斯：出正，看似回报高终是输之；出反，看似回报低终是胜之。李斯说要选择赢面大的一方，韩非回应：胜与败或许早已注定。

这一集的小标题下面的话是：“规则的制定往往是用来掩盖游戏的本质，用来迷惑那些执着于胜负的人。”

（三）三姬分金论规则

在天行九歌第7集里有三姬分金的故事，本质上是海盗分金的演绎。

一艘行驶在大海上的三个海盗要分配100枚金币。第一个海盗提出分配方案，如果超过一半的人同意他的方案，就按照这个方案分配，否则就把他扔下船去喂鲨鱼，由第二的强盗提出新的分配方案，直到得到大多数人同意的方案。

第一个强盗应该提出什么样的分配方案呢？

第一个强盗会给自己99枚金币，给第二个强盗1枚金币，第三个强盗没有金币。第二个强盗会赞同第一个强盗的方案，因为如果第一个强盗被扔进了海里，由他提出方案时，无论他提出什么样的方案，第三个强盗都可能拒绝并把他扔进海里，而同意第一个强盗的方案，不仅不用承担被喂鲨鱼的风险，而且可以有一枚金币的收益。

如果是四个强盗在大海上分配这100枚金币。第一个强盗要怎么分呢？

第一个强盗给自己97枚金币，给第二个强盗0枚金币，给第三个强盗2枚金币，给第四个强盗1枚金币。

这样的分配方案，第二个强盗一定是拒绝的。如果第三个和第四个强盗也拒绝的话，则第一个强盗被扔下船去，回到三个强盗在船上分配金币的情形，第三个强盗只能得到1枚金币，而第四个强盗根本得不到金币。由于相比较下，这样的收益更多，第三个和第四个强盗就会同意第一个强盗的方案。这样四个人里面已经有三个人同意了，第二个人同意不同意就不重要了。

整个游戏的规则基础是少数服从多数。默认少数服从多数是一种公平，就是造成这种并不公平的分配的基石。少数服从多数更像是一种恃强凌弱，本质上与“强者可以随时改变规则，而弱者根本没有资格来制定规则”并无不同。而当一种游戏的规则通行时，往往只有规则的制定者能够获得最大的收益。