机器学习时间序列之KLMS,KRLS, QKLMS和MCC

手稿均来自Principe大佬, 硕士上过他的机器时间序列。大佬对kernel空间的LMS很有研究。

附上老师的首页

RKHS 希尔伯特核再生空间

Reproducing Kernel Hilbert Spaces

1. 希尔伯特空间是一个完备的内积空间
   
2. 线性泛函将希尔伯特空间映射到实数集，并且此泛函是连续,有界的, 此时就变成了RKHS
   

KLMS

1. 线性LMS的缺点，速度受到特征值(${\lambda }_{min}$)的控制
   
2. 神经网络和核函数滤波对比，核方法会模型会变大，但是满足凸优化，不需要正则化(KLMS)

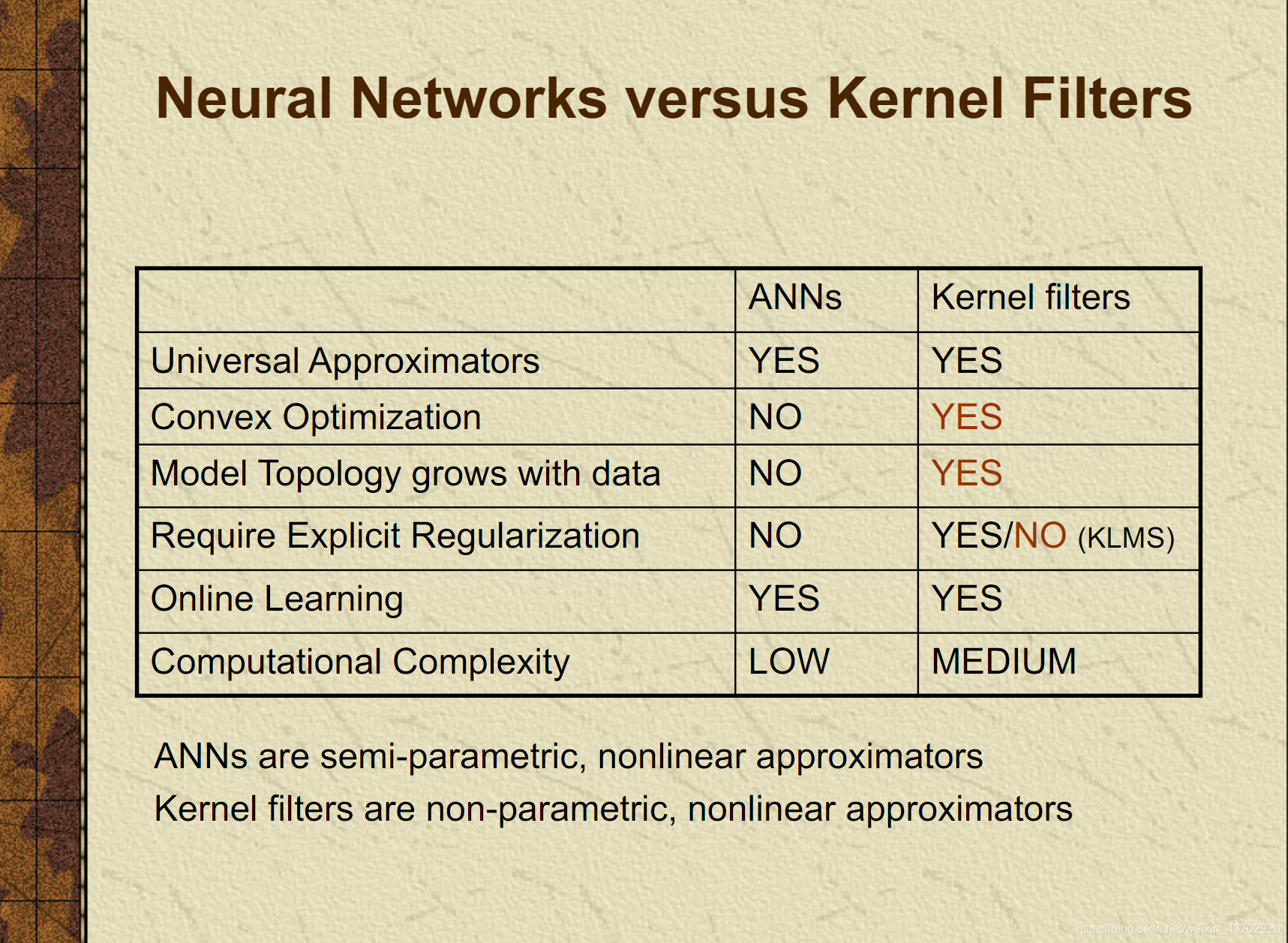
3.核方法

4. KLMS: w是不能直接算出来的，只能直接得到预测的函数f。衡量每次当前的数据点，与过去的点的误差*核函数之和。

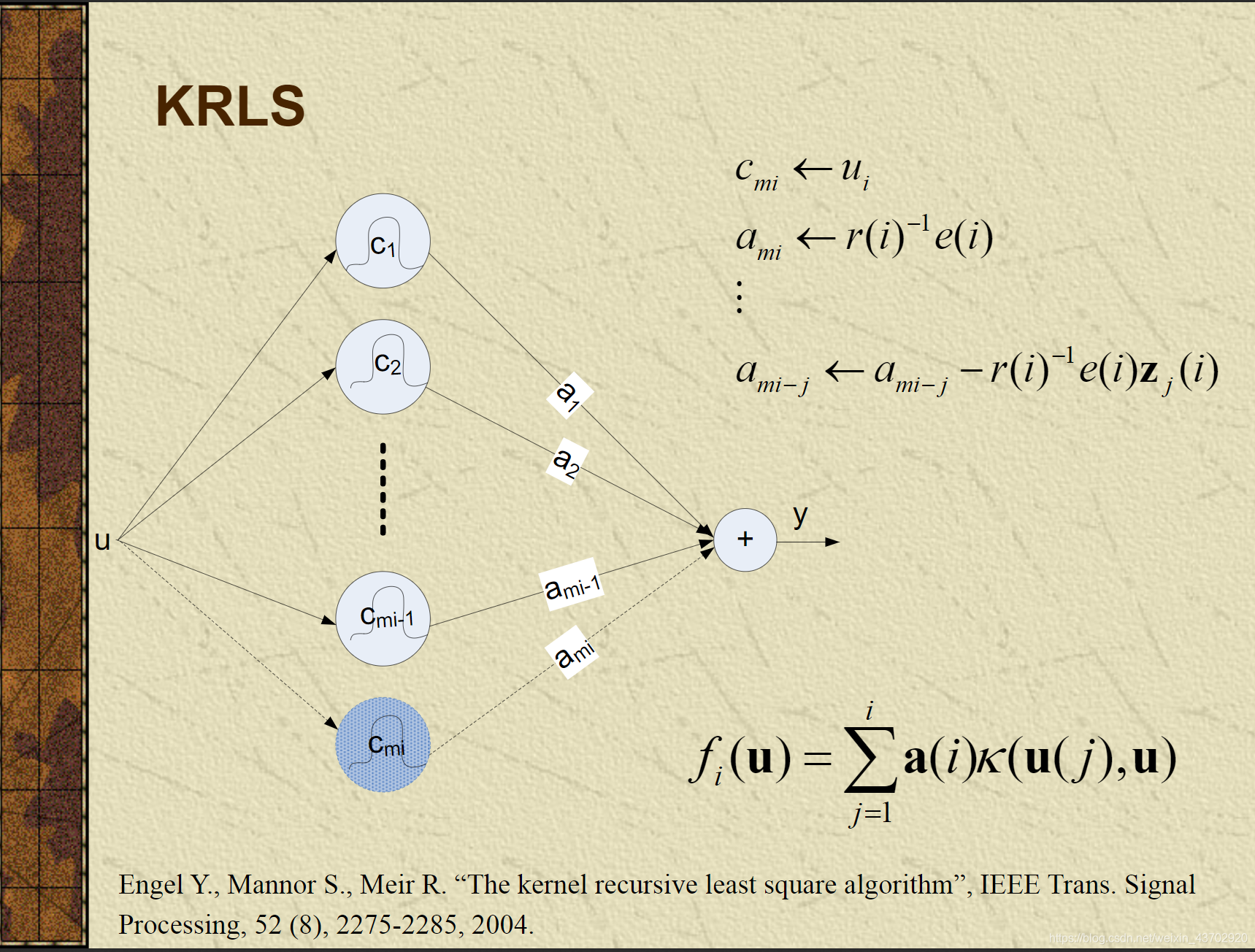
KRLS

1. RLS:利用了二阶导，逆矩阵定理，更新每次的自相关矩阵
2. Kernel化
   
   

QKLMS

1. 之前每进来一个点，都要作为中心，用来衡量计算。这样网络大小会累加到很大！计算变多
2. 因此，我们要减少作为中心的点的数目。
   
3. 然后如果进来一个数据点，它和之前的点很接近，我们不把它加入到=={Center}==集合里，只更新对应center的误差！
4. 这样，网络大小变小了
   

MCC

1. 基础: KL散度 = 交叉熵+熵
   
2. 相关熵
   
   
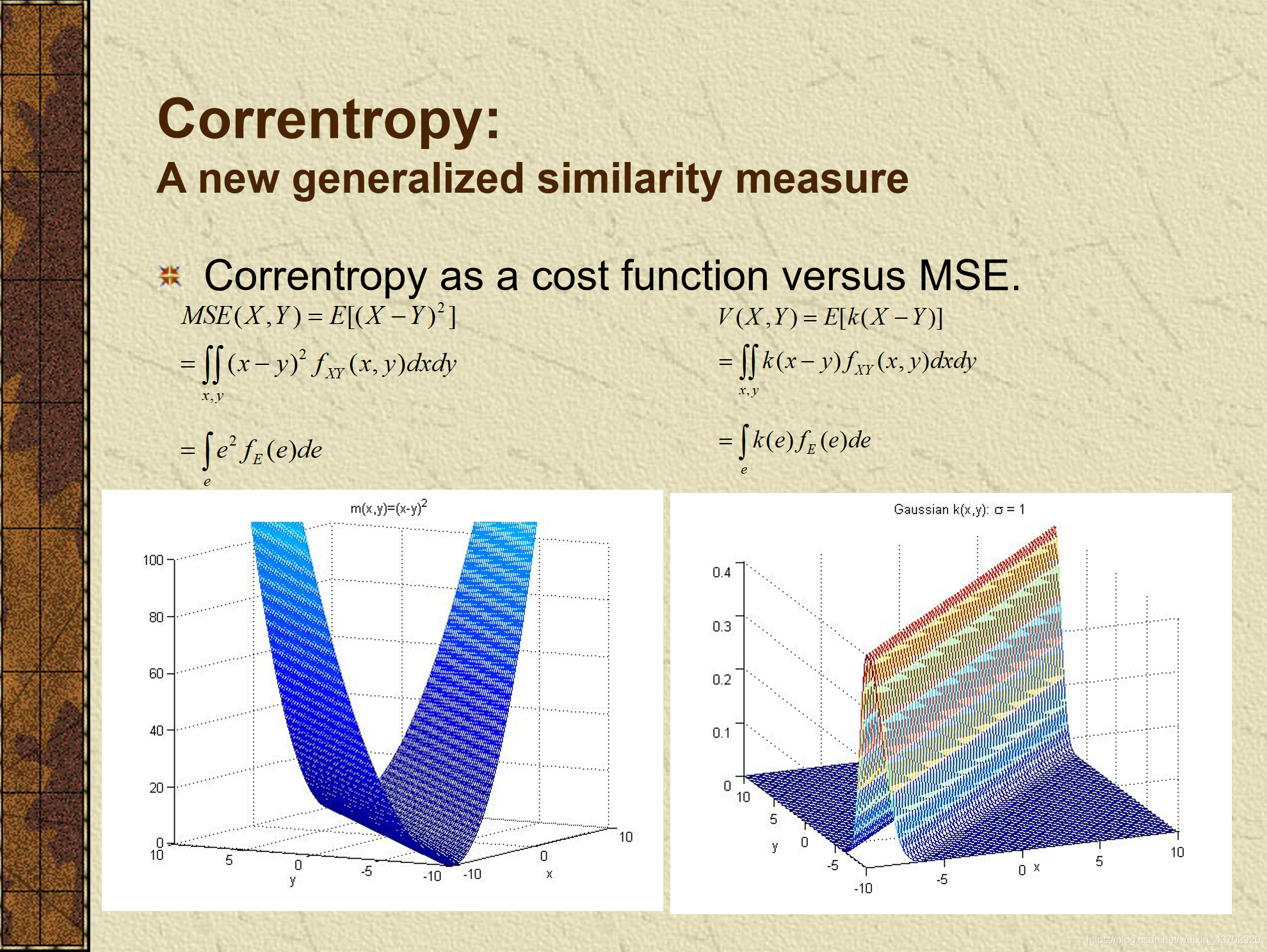
3. 最小化高斯函数的代价 == 最大化误差的相关熵