数字序列问题

解题思路：

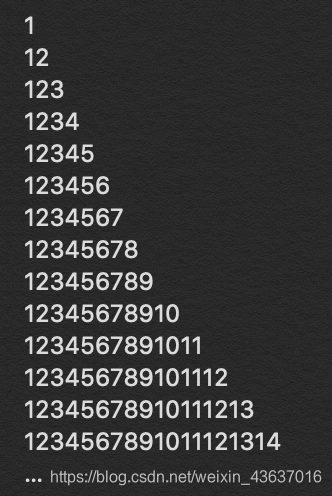
这个序列的结构如上图所示，很明显求解第k个数字是什么需要分两步走，第一步求解所在的行，第二部求解所在的列即该行中的什么位置。首先看怎么求解第k个数字所在的行，我们发现当某一行的最后一个数的位数为w时，这一行的数字个数与相邻行的数字个数的差为w，即局部范围内成等差数列（具有相同位数的最后一个数的行）。我们就按照每行的最后一个数的位数来划分所有的这些行使得它们组成一个个的等差数列。根据等差数列求和公式计算出每一个以x为结尾的行的所有前缀的和（包括整个这一行本身）。用count1函数来实现，其中x为该行的最后一个数字，w为位数，ans为以x为结尾的行的所有前缀的和（包括整个这一行本身），pre为当前前缀和，line为行数，cline为已经记录过得行数，t为x的拷贝。solve函数中执行第一步是采用二分来实现的这也是本题中的第一次二分，求出目标元素所在的行，然后对l和r进行更新准备第二次二分。第二部考虑这个元素在目标行中的位置，count2函数用来计算x的最后一位数在它所在的该行中的序列号，与count1计算方法类似，但不再存在前缀和pre，因为只需要考虑这一行即可。之后再次进行二分，搜索在目标元素在该行中的位置，注意找到的位置需要向后整体移动一个（ans++），然后将这个数ans转换成字符串，取第k个字符即为目标数字。
注意事项：
这道题直接搜素就很容易得到60%的分数，但想在数据量更大时不超时需要用两次二分查找的思想去二分查找目标数而不能在对应行中直接遍历搜索。二分时除以2可以采用右移1位的方法实现，同时数据范围达到10^18，需要使用long long类型数据。
总结：
一道有难度的题目，分组的思想很容易想到，等差数列的计算主要是数学思维的考察，注意公差的改变以及第二次搜索时与第一次搜索时的略微不同。同时通过两次二分可以降低时间复杂度不会在后几个评测点超时。考试时可能有同学觉得难度太大直接放弃其实很可惜，考试时我简单分组以后直接遍历每一行去搜索目标数也过了前60%的评测点。另外一定注意数据范围比较大时用long long类型数据，也不需要在不必要的时候所有数据都使用long long。int类型数据一般是在2x10^9以下的范围。
参考代码：

#include <iostream>
#include <string>
#include <cstring>
using namespace std;
long long count1(long long x){
   
    long long ans=0,pre=0,w=0,cline=1,line=