85. 最大矩形

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

int maximalRectangle(char** matrix, int matrixSize, int* matrixColSize){
    int row = matrixSize;
    if(row == 0)
    {
        return 0;
    }
    int line = matrixColSize[0];
    int dp[row][line];
    memset(dp, 0, sizeof(dp));
    int res = 0;

    for(int i = 0; i < row; i++)
    {
        for(int j = 0; j < line; j++)
        {
            if(matrix[i][j] == '1')
            {
                dp[i][j] = (j == 0 ? 1 : dp[i][j-1] + 1);  //寻找每行中连续的矩形
            }
        }
    }

    for(int i = 0; i < row; i++)
    {
        for(int j = 0; j < line; j++)
        {
            int width = dp[i][j];
            int maxares = width * 1;

            for(int k = i - 1; k >= 0; k--)
            {
                if(dp[k][j] == 0)
                {
                    break;
                }
                width = width  < dp[k][j] ? width : dp[k][j];  
                //向上寻找最大的矩阵
                maxares = width * (i - k + 1) > maxares ? width * (i - k + 1) : maxares;
            }

            res = res > maxares ? res : maxares;

        }
    }

    return res;
    
}

思路：动态规划
可以使用dp数组记录每行的连续的为1的数字，就可以得知每行中当前格子的前方有多少个连续为1的格子：

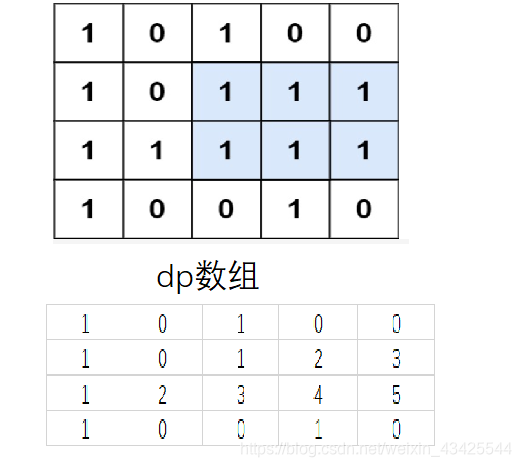
然后再从每个格子开始遍历，每次都向上一行遍历，查看有没有数值为1的格子，然后计算面积。