算法导论学习笔记12_动态规划

---

1. 动态规划的定义及步骤

动态规划（英语：Dynamic Programming，简称DP)常用于求解最优化问题。它与分治法相似，都是通过组合子问题的解来求解原问题。

分治法(Divide and Conquer)将问题划分为互不相交的子问题，递归地求解子问题，再将它们的解组合起来，求出原问题的解。动态规划用于子问题重叠的情况，而子问题重叠的含义是不同的子问题有公共的子子问题。对于这些公共的子问题，只需要求解一次并将其解存储起来，当再次遇到该子问题时，直接返回之前存储的结果即可。

下面通过斐波那契数列的例子说明什么时候该用动态规划而不是分治法：

斐波那契数列(Fibonacci sequence)是一个通过递归的方式定义的数列，形式如下：

斐波那契数列数列中，除了前两个元素外，所有的元素为前两个元素之和，递归式如下：$$F_n=\{\begin{array}{ll}0& n=0\\ 1& n=1\\ F_{n-1}+F_{n-2}& n\ge 2\end{array}$$
例如，斐波那契数列的第6项值为8，是第4项和第5项的值3和5之和。

下面用典型的分治步骤来分析求解斐波那契数列的第n项：
分解：将$F_n$的求解分解为求解更小规模的问题$F_{n-1}$和$F_{n-2}$。
解决：递归地求解$F_{n-1}$和$F_{n-2}$，当$n<2$时，停止递归。
合并：将$F_{n-1}$和$F_{n-2}$的值求和得到$F_n$的值。

int Fibonacci(int n) {
	int Fib_n, Fib_n_1, Fib_n_2;
	if (n < 2) return n;
	// Divide and Conquer
	Fib_n_1 = Fibonacci(n - 1);
	Fib_n_2 = Fibonacci(n - 2);
	// Merge
	Fib_n = Fib_n_1 + Fib_n_2;
	return Fib_n;
}

以$n=6$为例，绘制出递归树如下：

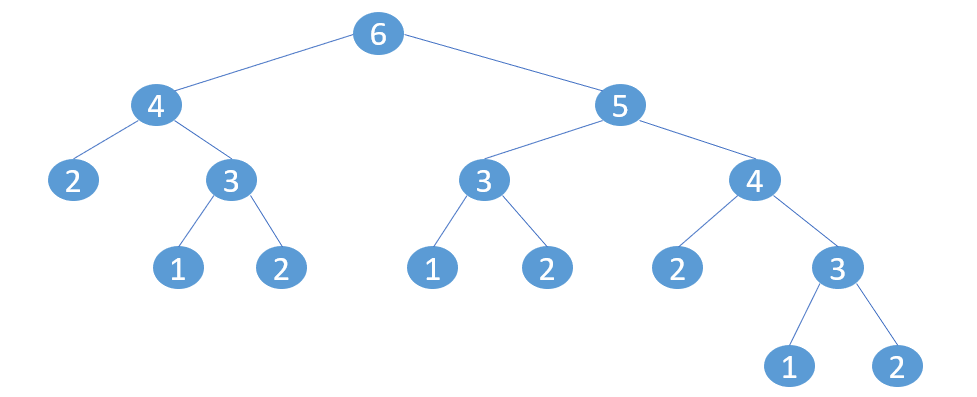
从递归树可以看出，除了Fibonacci(6)和Fibonacci(5)以外，其他所有子问题都被重复解决了多次。如Fibonacci(4)计算了2次，Fibonacci(3)被计算了3次，Fibonacci(2)被计算了5次…

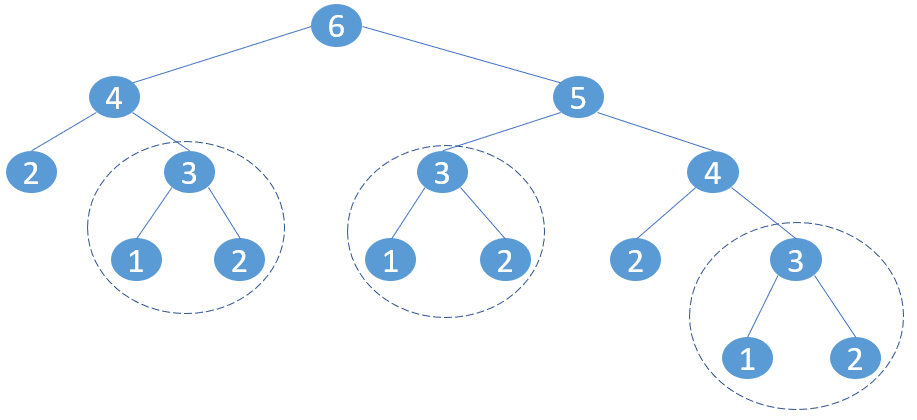
通过分析可知，子问题Fibonacci(4)和Fibonacci(5)都包含子问题Fibonacci(3)(虚线框部分)，而子问题Fibonacci(3)还递归的包含了子问题Fibonacci(2)和Fibonacci(1)。这种情况被称为子问题重叠，对于这些重叠的子问题，我们只需要计算一次，然后存储它们的计算结果，当再次遇到相同子问题时，直接返回存储的解即可，这正是动态规划的核心思想。

动态规划算法的设计通常由以下4个步骤组成：

1. 刻画一个最优解的结构特征。
2. 递归地定义最优解的值。
3. 计算最优解的值，通常采用自底向上的方法。
4. 利用计算出的信息构造一个最优解。

其中，步骤4通常可以省略，因为有时候只需要计算出最优解的值而不是最优解本身。当需要得到最优解本身的时候需要在步骤3的过程中维护一些额外信息，以便于用于构造一个最优解。

2. 实例1：钢条切割

问题如下：给定一段长度为$n$的钢条和一个价格表$p$，价格表$p$中为各个长度的钢条的价格$p_i$。现将该钢条切割为若干段，则该钢条切割之后的总价格为各段价格之和。求切割钢条的方案，使得各段价格之和最大。

例如，对于一段长度$n=3$的钢条，切割方案有 { 3 } , { 1 , 2 } , { 2 , 1 } , { 1 , 1 , 1 } \{3\},\{1, 2\},\{2, 1\},\{1,1,1\} {3},{1,2},{2,1},{1,1,1}四种，它们的总价格分别为$8,6,6,3$，因此最优切割方案为 { 3 } \{3\} {3}，即不切割。

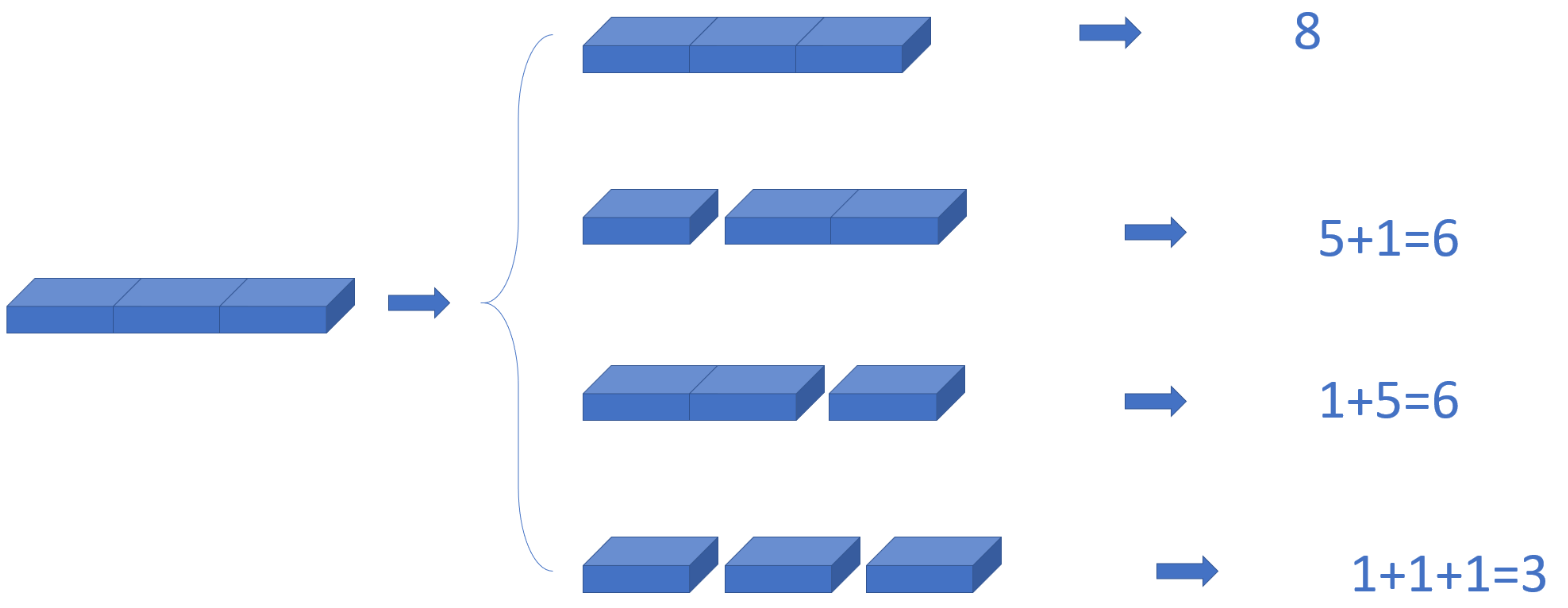
动态规划第一步：刻画一个最优解的结构特征。
通过分析可知，无论是哪种切割方案，切割之后的第一段钢条的长度范围为1-10。因此，我们可以把原问题转换为如下问题：将钢条切割为两个部分，第一个部分只有一段，其长度$i\le 10$，第二个部分可切割为若干段，总长度为$n-i$。那么第一部分的价格为$p_i$，第二个部分的价格为求解规模较小的相同问题$n=n-i$。因此，可以递归的定义最优解的值：$$r_n=\underset{1\le i\le min(n,10)}{\max }(p_i+r_{n-i})$$注：当$n\le 10$时，$i\in [1,n]$；$n>10$时，$i\in [1,10]$。

另一种思路是：将钢条分割为两个部分，第一个部分长度为$i$，第二个部分长度为$n-i$，因此原问题就转换为求解两个规模较小的相同问题$i$和$n-i$，最优解是：$$r_n=\{\begin{array}{ll}\underset{1\le i\le n-1}{\max }(r_i+r_{n-i})& n>10\\ \max (p_n,\underset{1\le i\le n-1}{\max }(r_i+r_{n-i}))& n\le 10\end{array}$$
注：当$n\le 10$时，还需要考虑到可能不分割时可能取得最大利益。

根据上述思路，可以很容易的用递归法求得最优解：

int cut(int p[], int n) {
	if (n == 0) return 0;
	int Max = -1;
	for (int i = 1; i <= (n > 10 ? 10 : n); i++) {
		Max = max(Max, p[i] + cut(p, n - i));
	}
	return Max;
}

下面绘制出$n=4$时的递归树：

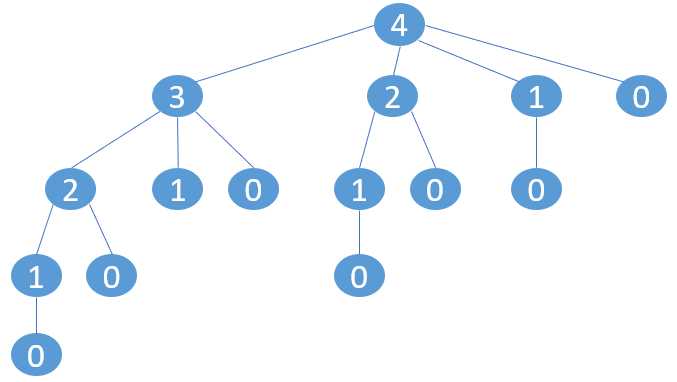
从递归树中可以看出，同求解斐波那契数列时的递归树一样，其中对相同的子问题进行了多次计算，因此浪费了许多性能。可以证明，这种朴素的递归方法的运行时间并不优于枚举方法，其运行时间为$\Theta (2^n)$，当n比较大时，运行时间非常长。

使用动态规划求解最优钢条切割问题
递归算法之所以效率很低，是因为他们反复求解相同的子问题。而动态规划对每个子问题只求解一次，并将结果保存下来，如果再次遇到相同的子问题，则直接返回存储的结果即可，而不需要再次求解。

因此，动态规划是一个空间换时间的典型例子。

动态规划有两种实现方法：

①带备忘的自顶向下方法：此方法求解问题的过程和朴素递归方法相同，但递归的过程中会保存子问题的解。当需要一个子问题的解时，首先查询是否已经保存过该子问题的解，如果是，则直接返回该子问题的解。

下面是钢条切割问题的代码：

int cut_up_bottom_use(int p[], int n, int r[]) {
	if (r[n] > -1) return r[n];
	if (n == 0) return r[0] = 0;
	int Max = -1;
	for (int i = 1; i <= (n > 10 ? 10 : n); i++) {
		Max = max(Max, p[i] + cut_up_bottom_use(p, n - i, r));
	}
	return r[n] = Max;
}
int cut_up_bottom(int p[], int n) {
	int *r = new int[n + 1];
	for (int i = 0; i <= n; i++) r[i] = -1;
	return cut_up_bottom_use(p, n, r);
}

程序中利用辅助数组r[1…n]来保存子问题的解，因此在函数开始时先判断数组r是否保存了该问题的解，如果有的话直接返回r[n]的值，否则的话再继续进行求解。
②自底向上法：朴素方法在求解问题时会递归依赖更小规模的子问题的解，真正的动态规划是按问题的规模由小到大的顺序求解。当需要求解某个问题时，其更小规模的子问题已经求解完毕，因此可以通过查询得到结果。

下面是代码：

int cut_bottom_up(int p[], int n) {
	int *r = new int[n + 1];
	r[0] = 0;
	for (int j = 1; j <= n; j++) {
		int Max = -1;
		for (int i = 1; i <= (j > 10 ? 10 : j); i++) {
			Max = max(Max, p[i] + r[j - i]);
		}
		r[j] = Max;
	}
	return r[n];
}

程序中外层循环是按1…n的由小到大顺序依次求解$r_1...r_n$，当求解问题$r_i$时，比其规模更小的子问题已经解决过了，因此直接查询数组$r[0..n]$即可。

下面是对朴素递归法、自顶向下动态规划和自底向上自动规划三种方法运行时间的测试，可以看到当问题的规模增加1时，朴素递归算法的运行时间会翻倍，而使用动态规划算法求解本题的运行时间几乎可以忽略不计。经过测试，当$N=10000$时，动态规划算法的运行时间仍然在毫秒级。

注：自底向上算法和自顶向下算法具有相同的渐近运行时间，但自底向上算法的优势在于可以节省递归时所损耗的时间和空间，并且当问题的规模过大时，递归算法可能导致栈溢出(stack overflow)。因此，自底向上的动态规划算法往往比自顶向下的算法更加高效。

重构解
前面的过程已经完成了动态规划所必须的三个步骤：

1. 刻画一个最优解的结构特征。
2. 递归地定义最优解的值。
3. 计算最优解的值，通常采用自底向上的方法。

而上述三个步骤仅仅得出了问题的最优解的值，也就是最优钢条分割的总价值，而没有得到最优解本身，也就是分割的方案。因此，还需要对上述动态规划算法进行拓展，使之能够重构出最优解。

重构解往往需要在程序的运行过程中保存一些信息，在算法找到最优解时，通过这些信息可以重构出最优解本身。下面通过保存每个子问题分割的第一段钢条的长度$s_i$来重构解。

#include <iostream>
using namespace std;
int *r, *s;
int cut_bottom_up(int p[], int n) {
	r = new int[n + 1];
	s = new int[n + 1];
	r[0] = 0;
	for (int j = 1; j <= n; j++) {
		int Max = -1;
		for (int i = 1; i <= (j > 10 ? 10 : j); i++) {
			if (Max < p[i] + r[j - i]) {
				Max = p[i] + r[j - i];
				s[j] = i;
			}
			r[j] = Max;
		}
	}
	return r[n];
}
void cut_bottom_up_restruct(int n) {
	while (n > 0) {
		cout << s[n] << " ";
		n = n - s[n];
	}	
}
int main(int argc, char* argv[]) {
	int p[11] = { 0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30 };
	cout << "Result:" << cut_bottom_up1(p, 33) << endl;
	cout << "Solution:";
	cut_bottom_up_restruct(33);
	return 0;
}

当$n=33$时，输出结果为：

Result:98
Solution:3 10 10 10

3. 实例2：矩阵链乘

问题描述：给定一个$n$个矩阵的序列$<A_1,A_2,...,A_n>$，希望计算它的乘积：$$A_1{A}_2...A_n$$我们知道，对于矩阵链乘$A_1{A}_2{A}_3$，按照$((A_1{A}_2)A_3)$的顺序计算和按照$(A_1(A_2{A}_3))$的顺序计算得到的结果是相同的，其运算量与矩阵的维数有关。
假如三个矩阵的维数分别为：10×100、100×5和5×50。
按照$(A_1{A}_2)A_3$的顺序计算所需要的标量积的次数为10×100×5+10×5×50=7500；
按照$(A_1{A}_2)A_3$的顺序计算所需要的标量积的次数为100×5×50+10×100×50=75000；
因此，前一种方案要比后一种方案快10倍。

矩阵链乘问题：给定$n$个矩阵的链$<A_1,A_2,...,A_n>$，矩阵$A_i$的规模为$p_{i-1}\times p_i(1\le i\le n)$，试寻求最佳的链乘顺序，使得所需的标量乘法的次数最少。

1. 刻画一个最优解的结构特征
对于矩阵链$<A_1,A_2,...,A_n>$,我们可以找到一个分隔点$i$，使得原问题分解为两个规模更小的问题：$$(A_1..A_i)(A_{i+1}..A_n)$$
其中$<A_1..A_i>$$<A_{i+1}..A_n>$则是两个规模更小的子问题。
因此，我们只需要找到最优的分隔点$i$和两个子问题$<A_1..A_i>$$<A_{i+1}..A_n>$的最优解便可以得到原问题的解。

2. 递归的定义最优值的解
假设矩阵链$<A_i...A_j>$的最优解为$m[i,j]$，因此可以得到最优解的递归定义如下：$$m[i,j]=\underset{i\le k<j}{\min }(m[i,k]+m[i+1,j]+p_{i-1}{p}_k{p}_j)$$其中，$A_i$的维数为$p_{i-1}\times p_i$，因此$(A_i...A_k)(A_{k+1}...A_j)$所需标量乘法为 ：$p_{i-1}{p}_k{p}_j$。

3. 计算最优解的值
采用自底向上的动态规划算法来求得最优解，这里利用数组$m[0...n,0...n]$来保存起止位置分别为$i$和$j$的矩阵链的最优解，数组$s[1..n-1,2..n]$来保存$m[i,j]$的分隔点用于重构解。
此外，程序的输入为$p[0..n]$，代表输入矩阵链的维度。

#include <iostream>
#include <vector>
#include <climits>
using namespace std;
class matrix_chain {
private:
	int **m, **s;
	void init(int n);
public:
	int solution(vector<int> p);
};
void matrix_chain::init(int n) {
	// Dynamically creating a two-dimensional array
	m = new int* [n + 1];
	s = new int* [n + 1];
	for (int i = 0; i <= n; i++) {
		m[i] = new int[n + 1];
		s[i] = new int[n + 1];
	}
}
int matrix_chain::solution(vector<int> p) {
	int n = p.size()-1;
	init(n);
	for (int i = 1; i <= n; i++) m[i][i] = 0;
	for(int l = 2; l <= n; l++){
	// 按长度自底向上计算
		for (int i = 1; i <= n - l + 1; i++) {
			int j = i + l - 1;
			m[i][j] = INT32_MAX;
			for (int k = i; k <= j - 1; k++) {
				int q = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
				if (q < m[i][j]) {
					m[i][j] = q;
					s[i][j] = k;
				}
			}
		}
	}
	return m[1][n];
}

int main(int argc, char* argv[]) {
	matrix_chain M;
	vector<int> p = { 30, 35, 15, 5, 10, 20, 25 };
	cout << M.solution(p);
	return 0;
}

4. 重构解
前面通过自底向上的动态规划算法得到了最优解的值，也就是最少的标量乘法次数，但并没有得出链乘的顺序。在第3步中，为了在得到最优解之后能够重构出最优解，利用数组s存储了不同起始位置的最优分隔点。因此我们可以通过该信息来重构出最优解。

void matrix_chain::restruct(int i, int j) {
	if (i == j)
		cout << "A";
	else {
		cout << "(";
		restruct(i, s[i][j]);
		restruct(s[i][j] + 1, j);
		cout << ")";
	}
}

上述代码通过递归的方式输出了矩阵链乘的最优方案，程序的输出为：

15125：((A(AA))((AA)A))

因此，最优的方案为$((A_1(A_2{A}_3))((A_4{A}_5)A_6))$，该方案所需的标量乘法次数为15125次。

4. 动态规划的要素

通过前面的几个实例可以看到，利用动态规划解决问题的基本步骤为：

1. 刻画一个最优解的结构特征。
2. 递归地定义最优解的值。
3. 计算最优解的值，通常采用自底向上的方法。
4. 利用计算出的信息构造一个最优解。

这4个步骤告诉了我们如何设计动态规划算法，但没告诉我们动态规划算法适用于哪些问题，如何判断能够使用动态规划解决特定问题等。下面是合适应用动态规划算法求解的最优化问题应该具备的两个要素：最优子结构和子问题重叠。

最优子结构
从动态规划算法的设计步骤可以看出，应用动态规划求解最优化问题的第一步便是刻画一个最优解的结构特征。如果一个问题的最优解包含其子问题的最优解，我们就称此问题具有最优子结构。

如：钢条切割问题中，原问题的解$r(n)$可以理解是寻找一个切割点，使得第一段长度为$i$的钢条的价格$p_i$和余下长度为$n-i$的钢条的最优解$r(n-i)$之和$p_i+r(n-i)$具有最大值。也就是：$r(n)=\max (p_i+r(n-1))$。因此，原问题的最优解$r(n)$包含其子问题的最优解$r(n-i)$，因此钢条切割问题就具有最优子结构。同样的，矩阵链乘积问题也具有最优子结构。

通过上述描述可知，最优子结构是用来描述一个问题的性质，如果一个问题的最优解包含其子问题的最优解，那么这个问题就具有最优子结构性质。

在发掘最优子结构性质的过程中，遵循以下通用模式：

1. 证明问题最优解的第一个组成部分是做出一个选择。例如，钢条分割问题最优解的第一个组成部分是选择第一段的长度，矩阵链乘问题最优解的第一个组成部分是选择矩阵链的划分位置等。
2. 对于给定问题，在其可能的第一步选择中，假定已经知道那种选择才能得到最优解。
3. 给定可获得最优解的选择后，确定这次选择会产生哪些子问题。
4. 证明作为构成原问题最优解的组成部分，每个子问题的解都是它本身的最优解。

精简的来说就是：①做出选择；②假设选择可得最优解；③确定产生的子问题；④证明每个子问题的解都是它本身的最优解。

证明第4点可采用"剪切-粘贴"技术进行反证：假设子问题的解不是其自身的最优解，那么将这些解从原问题的最优解中"剪切"掉，然后将它们的最优解“粘贴”进去，从而得到一个更优的解，因此原问题的解不是最优解。

在动态规划算法中，通常采用自底向上地使用最优子结构。首先求得子问题的最优解，然后求原问题的最优解。在求解原问题过程中，需要在设计的子问题中做出选择，选择能得到原问题最优解的子问题。原问题最优解的代价通常就是子问题最优解的代价加上由此次选择直接产生的代价。

重叠子问题
子问题重叠是利用动态规划求解优化问题的第二个要素。如果递归算法反复求解相同的子问题，则称该问题具有重叠子问题性质。动态规划算法通常利用重叠子问题性质，对每个子问题求解一次，将解存入一个表中，当再次需要求解这个子问题时直接查表，且查表的时间为常量时间 。

一个问题是否适合用动态规划求解同时依赖于子问题的无关性和重叠性，重叠的意思是不同的子问题调用相同的子子问题，而无关性指的是不同子问题不共享资源。

5. 实例3：最长公共子序列

问题：给定两个序列$X=<x_1,x_2,...x_m>$和$Y=<y_1,y_2,...,y_n>$,求$X$和$Y$长度最长的公共子序列。
子序列定义：给定序列$X=<x_1,x_2,...x_m>$，另一个序列为$Z=<z_1,z_2,...,z_k>$，满足$z_1=x_a,z_2=x_b,...$，且$a,b,...$单调递增。则称序列$Z$为序列$X$的子序列。

例如：序列 X = { A , B , C , B , D , A , B } X = \{A, B, C, B, D, A, B\} X={A,B,C,B,D,A,B}，序列 Y = { B , D , C , A , B , A } Y=\{B, D, C, A, B, A\} Y={B,D,C,A,B,A}，它们的最长公共子序列长度为4，且有上述三种组成。

刻画最优解的结构特征
对于序列$X=<x_1,x_2,...x_m>$和$Y=<y_1,y_2,...,y_n>$，设其最长子序列为$L(m,n)$。如果$x_m=y_n$，则$L(m,n)=L(m-1,n-1)+1$；如果$x_m̸=y_n$，则$L(m,n)=\max (L(m-1,n)，L(m,n-1))$。

因此，原问题的最优解$L(m,n)$依赖于子问题$<m-1,n>$和$<m,n-1>$的最优解$L(m-1,n)$和$L(m,n-1)$。因此，此问题具有最优子结构的性质。

此外，$L(m-1,n)$依赖于$L(m-2,n)$和$L(m-1,n-1)$且$L(m,n-1)$依赖于$L(m-1,n-1)$和$L(m-2,n)$。可以看到，$L(m-1,n)$和$L(m,n-1)$依赖于相同的子问题$L(m-1,n-1)$，因此此问题具有子问题重叠的性质。

递归定义最优解的值
根据上述最优结构的性质，可得如下递归公式：$$L(i,j)=\{\begin{array}{ll}0& i=0或j=0\\ L(i-1,j-1)& i,j>0且x_i=y_j\\ \max (L(i-1,j),L(i,j-1)& i,j>0且x_i̸=y_j\end{array}$$
其中，若$i=0$或$j=0$，则最长公共子序列长度肯定为0，若$i,j>0$，则$L(i,j)$按$x_i$和$y_j$的取值依赖于不同的子问题。

计算最优解的值
利用上述递归公式可以很容易的写出自顶向下的带备忘的递归算法，但利用动态规划自底向上地进行计算往往会更加的高效。算法中需要利用一个数组$c[0..m,0..n]$来保存所有子问题的解的长度。此外，为了能够重构出解本身，还需要另一个辅助数组来记录每一步所作出的选择，这里所作出的选择为选择子问题$L(i-1,j)、L(i,j-1)、L(i-1,j-1)$中的哪一个，这里可以用$\uparrow 、\leftarrow 、\nwarrow$来表示。

自底向上的动态规划代码如下：

#include <iostream>
#include <vector>
using namespace std;

class LCS {
private:
	int **c, **r;
	const int LEFT = 1;
	const int UP = 2;
	const int LEFT_UP = 3;
	void init(int m, int n);
public:
	int solution(vector<char> X, vector<char> Y);
};
void LCS::init(int m, int n) {
	c = new int*[m+1];
	r = new int*[m+1];
	for (int i = 0; i <= m; i++) {
		c[i] = new int[n];
		r[i] = new int[n];
	}
	for(int i = 0; i <= m; i++)
		for (int j = 0; j <= n; j++)
		{
			r[i][j] = 0;
			c[i][j] = 0;
		}
}
int LCS::solution(vector<char> X, vector<char> Y) {
	int m = X.size();
	int n = Y.size();
	init(m, n);
	for(int i = 1; i <= m; i++)
		for (int j = 1; j <= n; j++) {
			if (X[i-1] == Y[j-1]) {
				c[i][j] = c[i - 1][j - 1] + 1;
				r[i][j] = LEFT_UP;
			}
			else {
				if (c[i - 1][j] > c[i][j - 1]) {
					c[i][j] = c[i - 1][j];
					r[i][j] = UP;
				}
				else {
					c[i][j] = c[i][j - 1];
					r[i][j] = LEFT;
				}
			}
		}
	return c[m][n];
}
int main(int argc, char* argv[]) {
	vector<char> X = { 'A', 'B', 'C', 'B', 'D', 'A', 'B' };
	vector<char> Y = { 'D', 'B', 'C', 'A', 'B', 'A' };
	LCS lcs;
	cout << lcs.solution(X, Y) << endl;
	return 0;
}

上述代码的输出结果为4，因此序列$X=<A,B,C,B,D,A,B>$和$Y=<D,B,C,A,B,A>$的最长公共子序列长度为4。

重构解
辅助数组r[0…m, 0…n]中保存了动态规划中所作出的选择，因此我们可以用递归的方式来重构解。

void LCS::restruct(int i, int j, const vector<char> &X) {
	if (i == 0 || j == 0) return;
	if (r[i][j] == LEFT_UP) {
		restruct(i - 1, j - 1, X);
		cout << X[i-1];
	}
	else if (r[i][j] == UP) restruct(i - 1, j, X);
	else restruct(i, j - 1, X);
}

重构解的过程如上述代码所示，由于数组r中保存了我们在递归过程中做出的最优选择，因此只需要根据该最优选择进行重构。如果$r[i][j]==LEFT\_UP$，说明$X[i-1]=Y[j-1]$，因此输出$X[i-1]$的值；如果$r[i][j]̸=LEFT\_UP$，则根据$r[i][j]$所指方向继续递归。

注：上述重构解的代码输出的最长公共子序列是逆序的。