算法导论学习笔记13_贪心算法

---

1. 贪心算法定义及性质

贪心算法（Greedy Method），又称为“贪婪算法”。是一种在每一步选择中都采取在当前状态下最好或最优的选择，从而导致结果是最好或最优的算法。

贪心算法的两个要素是：最优子结构、贪心选择性质。

最优子结构：如果一个问题的最优解包含其子问题的最优解，则称此问题具有最优子结构性质。此性质是能够应用动态规划和贪心算法的关键因素。

贪心选择性质：我们可以通过做出局部最优选择来构造全局最优解。换句话说，当我们进行选择时，只需要做出当前问题看起来最优的解，而不必考虑其子问题的解。

一个动态规划算法通常是自底向上计算的，而一个贪心算法通常是自顶向下的。

一般地，可以按如下步骤设计贪心算法：

1. 将最优化问题转换为如下形式：对其做出一次选择后，只剩下一个子问题需要求解。
2. 证明做出贪心选择后，原问题总是存在最优解，即贪心选择总是安全的。
3. 证明做出贪心选择后，剩余的子问题满足性质：其最优解与贪心选择组合即可得到原问题的最优解。

2. 实例1：活动选择问题

问题：有一个由多个活动构成的集合，各自有一个开始时间$s_i$和结束时间$f_i$，它们的开始时间和结束时间可能重叠，我们需要选出几个互不重叠的活动，且使得活动的数量达到最多。

注：活动已按结束时间排序。

动态规划解法1（书上的解法）：令$S_{ij}$表示在$a_i$结束之后开始，且在$a_j$开始之前结束的那些活动的集合。$A_{ij}$表示$S_{ij}$的一个最大的相互兼容的活动子集。例如，$S_{1,11}$表示在$a_1$结束之后开始，$a_{11}$开始之前结束的活动集合，因此 S 1 , 11 = { a 4 , a 6 , a 7 , a 8 , a 9 } S_{1,11}=\{a_4, a_6, a_7, a_8, a_9\} S1,11​={a4​,a6​,a7​,a8​,a9​}，且$A_{1,11}$至少包含$S_{1,11}$中的一个元素。设$A_{ij}$包含元素$a_k$，则可以得到两个子问题：寻找$S_{ik}$中的兼容活动以及$S_{kj}$中的兼容活动。

如果用$c[i,j]$表示集合$S_{ij}$的最优解的大小，则可得递归式$$c[i,j]=c[i,k]+c[k,j]+1$$
由于我们并不知道$a_k$取$S_{ij}$中的哪一个活动，因此需要考察其中的所有活动，因此
c [ i , j ] = { 0 S i j = ϕ max ⁡ a k ∈ S i j { c [ i , k ] + c [ k , j ] + 1 } S i j ≠ ϕ c[i,j] = \begin{cases}0&S_{ij}=\phi \\\max_{a_k\in S_{ij}}\{c[i,k]+c[k,j]+1\}&S_{ij}\neq\phi \end{cases} c[i,j]={0maxak​∈Sij​​{c[i,k]+c[k,j]+1}​Sij​=ϕSij​̸​=ϕ​
根据该递归式可以设计出动态规划算法：

void Solution::dp(vector<pair<int, int>> data) {
	int n = data.size();
	init(n);
	for (int l = 2; l < n; l++) // 按长度自底向上
		for (int i = 0; i < n - l; i++) {
			vector<int> S;
			for (int j = i + 1; j < i + l; j++) { // 构造集合S
				if (data[j].first >= data[i].second && data[j].second <= data[i + l].first) S.push_back(j);
				if (!S.empty()){
					int max = 0;
					for (int k : S) { // 考察S中的所有元素
						if (c[i][k] + c[k][i + l] + 1 > max) {
							max = c[i][k] + c[k][i + l] + 1;
							r[i][i + l] = k;
						}
					}
					c[i][i + l] = max;
				}
			}
		}
	restruct(data);
}

动态规划解法2：首先选择一个活动$a_k$作为第一个活动，则原问题转换为寻找活动$a_k$结束后开始的所有活动的最大兼容活动子集。由于不知道哪一个活动作为第一个活动时能够构造出最大的活动子集，因此需要对所有的活动进行考察。

自底向上的动态规划算法如下：

void AS::dp(const vector<pair<int, int>> &Activity) {
	// Dynamic programming
	int n = Activity.size();
	init(n);
	for (int i = n - 1; i >= 0; i--) { // 按结束时间自底向上
		for (int j = n - 1; j >= 0; j--) {
			int max = 0;
			if (Activity[j].first >= Activity[i].second) {
				if (c[j] + 1 > max) {
					max = c[j] + 1;
					c[i] = max;
					r[i] = j;
				}
			}
		}
	}
	restruct_dp(0, Activity);
}

贪心算法解法：从动态规划解法2中可以看出，如果我们每次都选择结束时间最早的活动（贪心选择），就能够剩下更多的时间来安排后续的活动。

贪心算法的递归解法如下：

vector<pair<int, int>> AS::gd(const vector<pair<int, int>> &Activity, int k) {
	int m = k + 1;
	int n = Activity.size();
	vector < pair<int, int>> buffer = { Activity[0] };
	while (m < n && Activity[m].first < Activity[k].second) m++;
	if (m < n) {
		buffer = select_gd(Activity, m);
		buffer.push_back(Activity[m]);
	}
	return buffer;
}

迭代解法如下：

vector<pair<int, int>> AS::select_gd1(const vector<pair<int, int>> &Activity) {
	int n = Activity.size();
	vector < pair<int, int>> buffer = { Activity[0] };
	int k = 0;
	for (int m = 1; m < n; m++) {
		if (Activity[m].first >= Activity[k].second) {
			k = m;
			buffer.push_back(Activity[m]);
		}
	}
	return buffer;
}

上述两种算法在进行选择时都采用的贪心策略，减少了时间和空间的损耗。

3. 实例2：霍夫曼编码

一个字符编码问题：对于一个100 000个字符的文件，只包含$a-f$ 6个不同字符，出现频率如下表所示。如果为每个字符指定一个3位的码字，可以将文件编码为300 000位的长度。但如果使用表中的变长编码，可以仅用224 000位长度即可。

注意：变长编码中的每一个编码都不是其它码字的前缀，这样在解码时才不会出现混乱。

用二叉树表示上述两种编码方式如下：

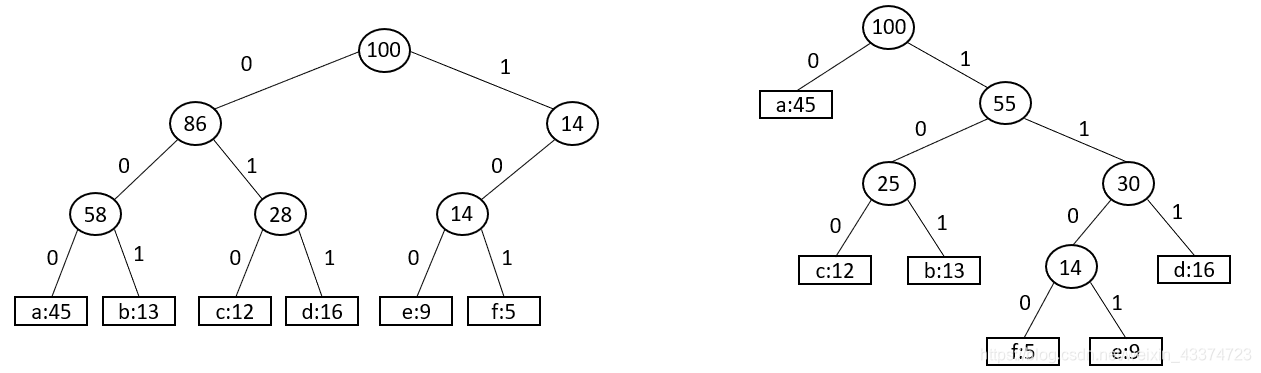
其中，左侧表示定长编码，所有叶子结点的深度相同。右侧表示变长编码，虽然看似树的深度更深，但由于频率越高的字符编码长度越短，因此变长编码具有更高的效率。此外，文件的最优编码方案总是对应一棵满二叉树，如右侧的二叉树所示。

霍夫曼设计了一个贪心算法来构造最优前缀码，被称为霍夫曼编码。下面是构造霍夫曼树的伪代码：

HUFFMAN(C)
	n = |C|
	Q = C
	for i = 1 to n - 1
		allocate a new node z
		z.left = x = EXTRACT_MIN(Q)
		z.right = y = EXTRACT_MIN(Q)
		z.freq = x.freq + y.freq
		INSERT(Q, z)
	return EXTRACT_MIN(Q)

其构造过程如下：

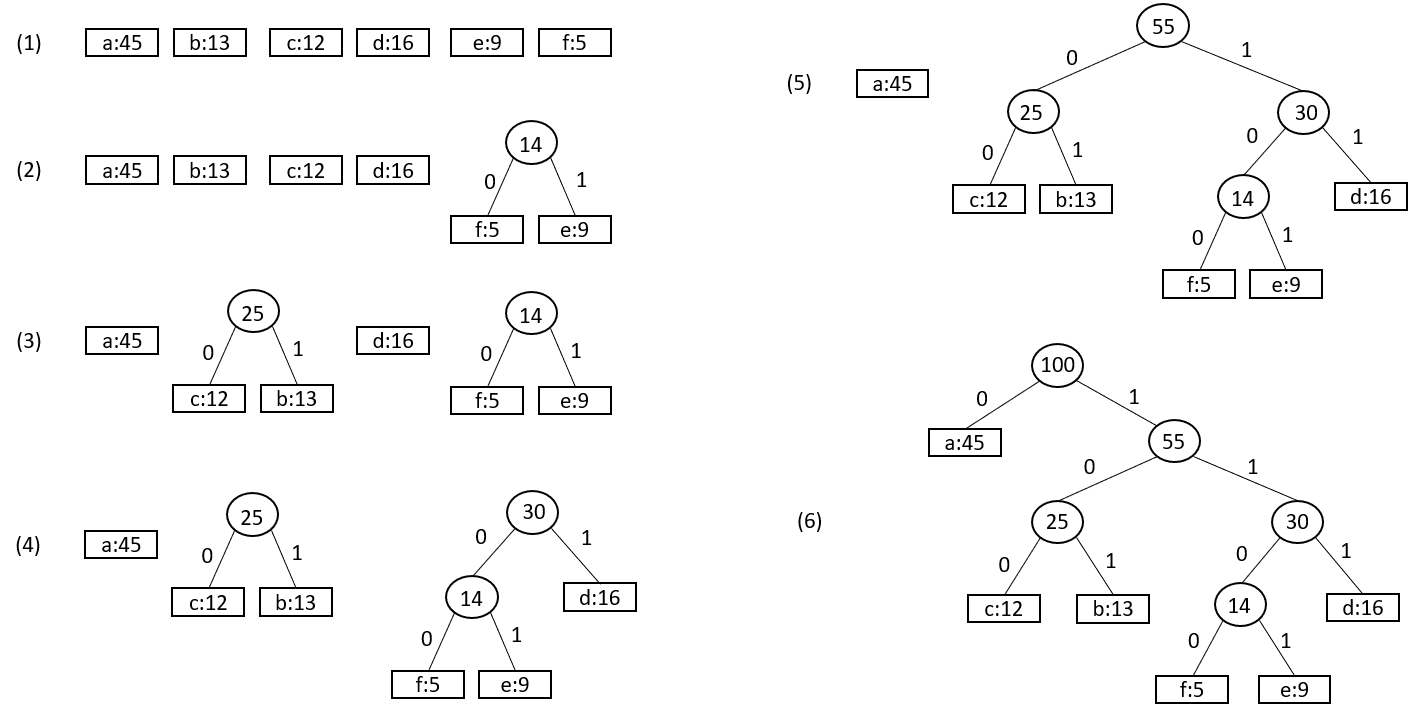
这里霍夫曼树的构造借助了优先队列，首先将所有的结点加入优先队列中，然后取出其中最小的两个结点并将它们合并为一个新的结点，将新结点加入优先队列后再次重复上过程，直到队列中只剩下一个元素为止。

4. 附录（代码）

4.1 活动选择代码

#include <iostream>
#include <vector>
#include <utility>
using namespace std;
class AS {
private:
	int *r, *c;
	void init(int n);
public:
	void dp(const vector<pair<int, int>> &Activity);
	void restruct_dp(int start, const vector<pair<int, int>> &Activity);
	vector<pair<int, int>> select_gd(const vector<pair<int, int>> &Activity, int k);
	vector<pair<int, int>> select_gd1(const vector<pair<int, int>> &Activity);

};
void AS::init(int n) {
	r = new int[n];
	c = new int[n];
	for (int i = 0; i < n; i++) c[i] = 1;
}
void AS::dp(const vector<pair<int, int>> &Activity) {
	// Dynamic programming
	int n = Activity.size();
	init(n);
	for (int i = n - 1; i >= 0; i--) { // 按结束时间自底向上
		for (int j = n - 1; j >= 0; j--) {
			int max = 0;
			if (Activity[j].first >= Activity[i].second) {
				if (c[j] + 1 > max) {
					max = c[j] + 1;
					c[i] = max;
					r[i] = j;
				}
			}
		}
	}
	restruct_dp(0, Activity);
}
void AS::restruct_dp(int start, const vector<pair<int, int>> &Activity) {
	int max = 0;
	int index = -1;
	int n = Activity.size();
	for (int i = 0; i < n; i++) {
		if (c[i] > max && Activity[i].first >= start) {
			max = c[i];
			index = i;
		}
	}
	cout << Activity[index].first << "," << Activity[index].second << "\t";
	if (index >= n - 1) return;
	restruct_dp(Activity[index].second, Activity);
}
vector<pair<int, int>> AS::select_gd(const vector<pair<int, int>> &Activity, int k) {
	// greedy method
	int m = k + 1;
	int n = Activity.size();
	vector < pair<int, int>> buffer = { Activity[0] };
	while (m < n && Activity[m].first < Activity[k].second) m++;
	if (m < n) {
		buffer = select_gd(Activity, m);
		buffer.push_back(Activity[m]);
	}
	return buffer;
}
vector<pair<int, int>> AS::select_gd1(const vector<pair<int, int>> &Activity) {
	// greedy method
	int n = Activity.size();
	vector < pair<int, int>> buffer = { Activity[0] };
	int k = 0;
	for (int m = 1; m < n; m++) {
		if (Activity[m].first >= Activity[k].second) {
			k = m;
			buffer.push_back(Activity[m]);
		}
	}
	return buffer;
}

int main(int argc, char* argv[]) {
	vector<pair<int, int>> Activity = {{1, 4}, {3, 5}, {0, 6}, {5, 7}, {3, 9}, {5, 9}, {6, 10},
										{8, 11}, {8, 12}, {2, 14}, {12, 16} };
	AS as;
	as.dp(Activity);
	vector<pair<int, int>> ret = as.select_gd1(Activity);
	for (int i = 0; i < ret.size(); i++) {
		cout << ret[i].first << "," << ret[i].second << "\t";
	}
	cout << endl;
	return 0;
}

4.2 霍夫曼编码代码

#include <iostream>
#include <queue>
#include <utility>
#include <string>
#include <map>
using namespace std;
struct Node {
	Node* left = nullptr;
	Node* right = nullptr;
	char ch = '\0';
	int freq = 0;
	Node(Node* l, Node* r, char c, int f)
		:left(l), right(r), ch(c), freq(f) {};
};
bool operator<(Node A, Node B) {
	return B.freq < A.freq;
}
class Huffman{
private:
	map<char, string> Map;
	priority_queue<Node> Q;
public:
	Node Tree_Build(vector<pair<char, int>> &data) {
		int n = data.size();
		for (int i = 0; i < n; i++) {
			Q.push(Node(nullptr, nullptr, data[i].first, data[i].second));
		}

		for (int i = 1; i < n; i++) {
			Node *node1 = new Node{ Q.top() }; Q.pop();
			Node *node2 = new Node{ Q.top() }; Q.pop();
			Node node(node1,node2, '\0', node1->freq + node2->freq);
			Q.push(node);
		}
		return Q.top();
	}
	void Map_Build(Node T, string str) {
		string s = str;
		if (T.ch != '\0') {
			Map.emplace(pair<char, string>{T.ch, str});
		}
		else {
			if (T.left != nullptr) {
				s.append("0");
				Map_Build(*(T.left), s);
				s.pop_back();
			}
			if (T.right != nullptr) {
				s.append("1");
				Map_Build(*(T.right), s);
			}
		}

	}
	void Init(vector<pair<char, int>> &data) {
		Node node = Tree_Build(data);
		Map_Build(node, "");
	}
	string Encoder(string str) {
		string s;
		for (auto ch : str) {
			s.append(Map.at(ch));
		}
		return s;
	}
	string Decoder(string str) {
		Node node = Q.top();
		Node* p = &node;
		string s;
		for (char ch : str) {
			if (p->ch != '\0') {
				s.push_back(p->ch);
				p = &node;
			}
			if (ch == '0') p = p->left;
			else p = p->right;
		}
		if (p->ch != '\0') s.push_back(p->ch);
		return s;
	}
};

int main(int argc, char* argv[]) {
	Huffman H;
	vector<pair<char, int>> data = { {'f', 5}, {'e', 9}, {'c', 12},{'b',13}, {'d', 16}, {'a', 45} };
	H.Init(data);
	string str = "abcdefabcdef";
	cout << "Encode: " << str << "->" << H.Encoder(str) << endl;
	string code = "001011011001001111111101110111001100";
	cout << "Decode: " << code << "->" << H.Decoder(code) << endl;
	return 0;
}