基于深度学习的单帧相位展开论文(2)

题目：Fringe pattern analysis using deep learning（2018）

原文地址

摘要

在许多光学计量技术中，条纹图案分析是从采集的条纹图案中恢复底层相位分布的核心算法。尽管数十年来进行了广泛的研究工作，如何从少数的条纹图案以尽可能高的精度提取所需的相位信息是具有挑战性的问题之一。受计算机视觉和其他应用深度学习技术最近成功的启发，我们首次证明深度神经网络可以被训练用来分析条纹，这大大提高了相位解调的准确性。在条纹投影轮廓测量场景下，利用载体条纹图案对所提方法的有效性进行了实验验证。实验结果表明，其在高精度和边缘保留方面优于两种代表性单帧技术：傅里叶变换轮廓测量法和窗口傅里叶轮廓测量法。

所提方法

在我们的方法中，网络配置受到大多数相位解调技术的基本过程的启发，简要回顾如下。典型条纹图案的数学形式可以表示为：
$$I(x,y)=A(x,y)+B(x,y)cos\varphi (x,y)\text{\hspace{1em}(1)}$$
其中，$I(x,y)$是条纹图像的强度；$A(x,y)$表示背景强度；$B(x,y)$表示调制强度；$\varphi (x,y)$表示所需相位分布。x和y表示该像素沿着水平和垂直方向的空间坐标。在大多数相位解调技术中，背景强度$A(x,y)$被视为干扰项，应从总强度中去除。然后，从反三角函数中恢复包裹相位图像，该函数的参数是一个比率，如下所示：
$$\varphi (x,y)=arctan\frac{M(x,y)}{D(x,y)}=arctan\frac{cB(x,y)sin\varphi (x,y)}{cB(x,y)cos\varphi (x,y)}$$
其中 c 是一个常数，具体取决于所使用的相位解调算法（例如，在 FTP 中 c = 0.5，在 N 步 相移法中 c = N/2 中），$M(x,y)$ 和 $D(x,y)$ 表示简写分别为分子和分母项。请注意，$M(x,y)$和$D(x,y)$ 的符号可进一步用于为 $\varphi (x,y)$ 的每次计算唯一定义象限。利用 4 象限相量空间，可以以 $2\pi$ 为模确定每个点的相位值。
为了模拟上述过程，构建了两个不同的卷积神经网络（CNN），并根据图1进行级联连接。

第一个卷积神经网络(CNN1)输入原始条纹图像$I(x,y)$并开始估计条纹图像的背景强度$A(x,y)$。利用估计的背景图像$A(x,y)$和原始条纹图像$I(x,y)$，训练第二个卷积神经网络 (CNN2) 来预测分子$M(x,y)$和分母$D(x,y)$，最后将其送入后续的反正切函数以获得最终的相位分布$\varphi (x,y)$。

为了生成用于训练两个卷积神经网络的地面实况数据，通过使用 N 步相移方法来实现相位检索。获取的对应的N个相移条纹图案可以表示为
$$I_n(x,y)=A(x,y)+B(x,y)cos[\varphi (x,y)-{\delta }_n]$$
其中$n=0,1,...,N-1$，${\delta }_n$是相移值($\frac{2\pi n}{N}$)。利用三角函数的正交性，可以得到背景强度：
$$A(x,y)=\frac{1}{N}\sum _{n=0}^{N-1}{I}_n(x,y)$$
利用最小二乘法，可以计算出相位：
$$\varphi (x,y)=arctan\frac{{\sum }_{n=0}^{N-1}{I}_n(x,y)sin{\delta }_n}{{\sum }_{n=0}^{N-1}{I}_n(x,y)cos{\delta }_n}$$
因此，方程中反正切函数的分子和分母可以表示为：
$$\begin{gathered} M(x,y)=\sum _{n=0}^{N-1}{I}_n(x,y)sin{\delta }_n=\frac{1}{N}B(x,y)sin\varphi (x,y) \\ D(x,y)=\sum _{n=0}^{N-1}{I}_n(x,y)cos{\delta }_n=\frac{1}{N}B(x,y)cos\varphi (x,y) \end{gathered}$$
简化表达式表明分子$M(x,y)$和分母$D(x,y)$与原始条纹图案密切相关。 通过与背景图像$A(x,y)$的准线性关系。因此，利用$A(x,y)$的知识，深度神经网络可以轻松学习 $M(x,y)$和$D(x,y)$，这再次证明了我们的网络设计的合理性。应该注意的是，简单的输入-输出网络结构[直接将条纹图案 $I(x,y)$ 链接到相位$\varphi (x,y)$] 在我们的例子中表现不佳，因为很难跟随相位缠绕（2π 跳跃）精确地在相位图中。因此，我们的深度神经网络不是直接估计相位，而是被训练来预测中间结果，即等式中反正切函数的分子和分母。


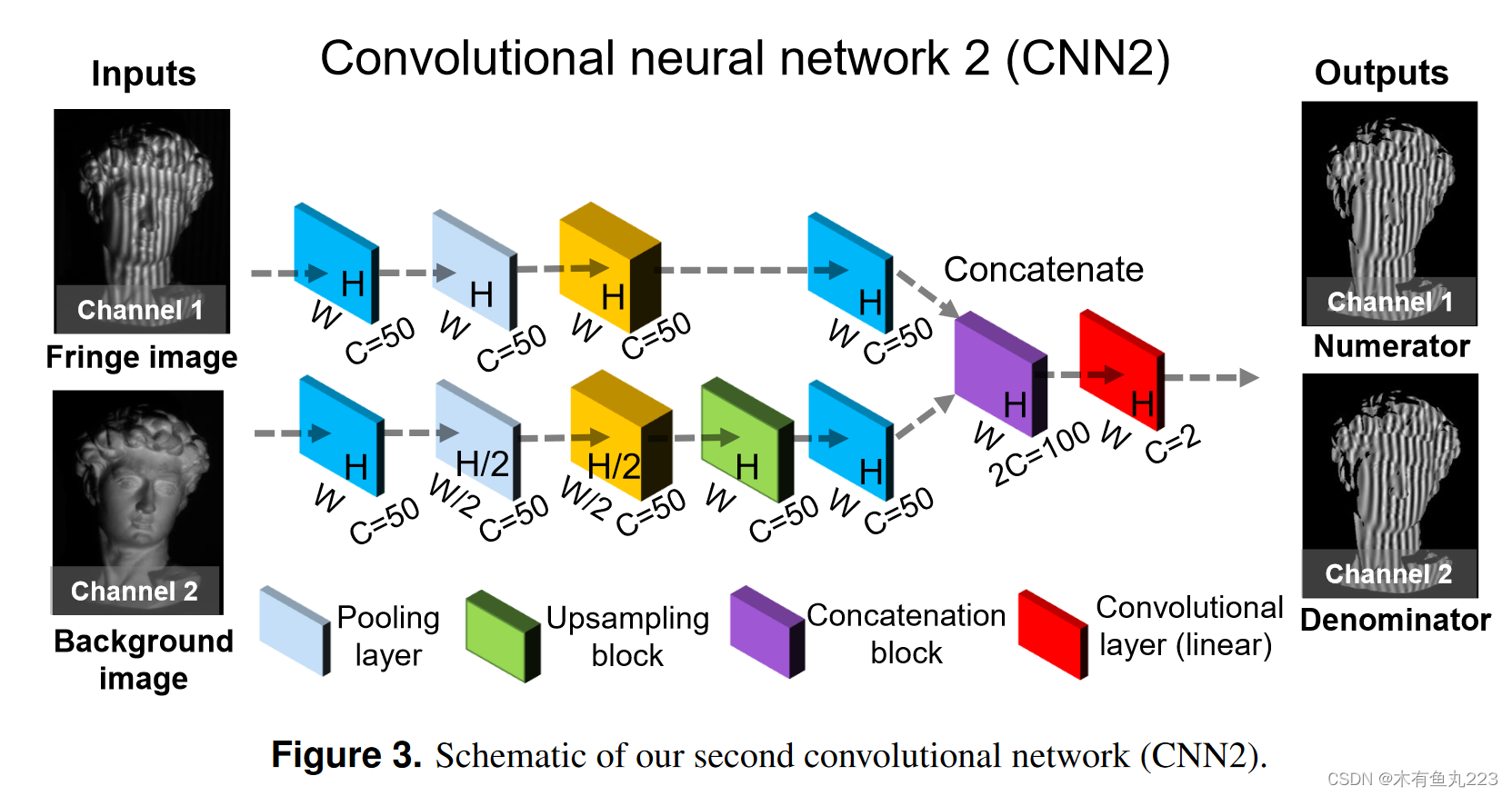
CNN1 的输入是具有 W × H 像素的原始条纹图案。然后依次经过一个卷积层、一组残差块（包含四个残差块）和两个卷积层进行处理。最后一层估计背景图像的灰度值。在CNN2中，输入图像在两个不同的路径中被下采样×1和×2。在第二条路径中，首先对数据进行下采样以实现高级感知，然后进行上采样以匹配原始维度。通过两个尺度的数据流路径，网络可以感知分子$M(x,y)$和分母$D(x,y)$的更多表面细节。

本文中所提出的结构CNN2的输入之一是CNN1输出的预测背景强度，因此首先通过监督学习的方法训练CNN1，而后使用预测的背景强度与采集到的条纹图案训练CNN2。实验结果如下Figure4所示。