1、线性代数的两种认知
数值层面:这是大部分课程中的教学内容,能解决计算、应用问题。但却不是最本质的内容,它是在给定法则下的运算。
几何层面:这个角度的线性代数可能更为接近本质,能帮助我们更好的认识线性代数这个工具,更好的使用它,知道为什么用,用什么,而不是单纯的如何计算。

2、什么是向量?
数值角度:它是一个有序的数值序列。
几何角度:它是空间中的一个带有指向的“箭头”,存在方向和长度。
以上两个观点是相互统一,可以互相转换的。而数学家给出的定义更为抽象,他们最终抽象出向量的两个关键运算:向量加法和向量数乘。只要加法和数乘两个运算就可以构成二维空间。
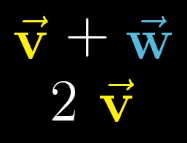
3、线性组合、空间与基
任何向量可由它所处的空间中的基向量(这两个基向量是不共线且不为0的向量,通常选用标准正交基)的线性组合表示。如向量[3,2] = 3i+2j。
采用数值描述一个向量时严格依赖于当前使用的基。
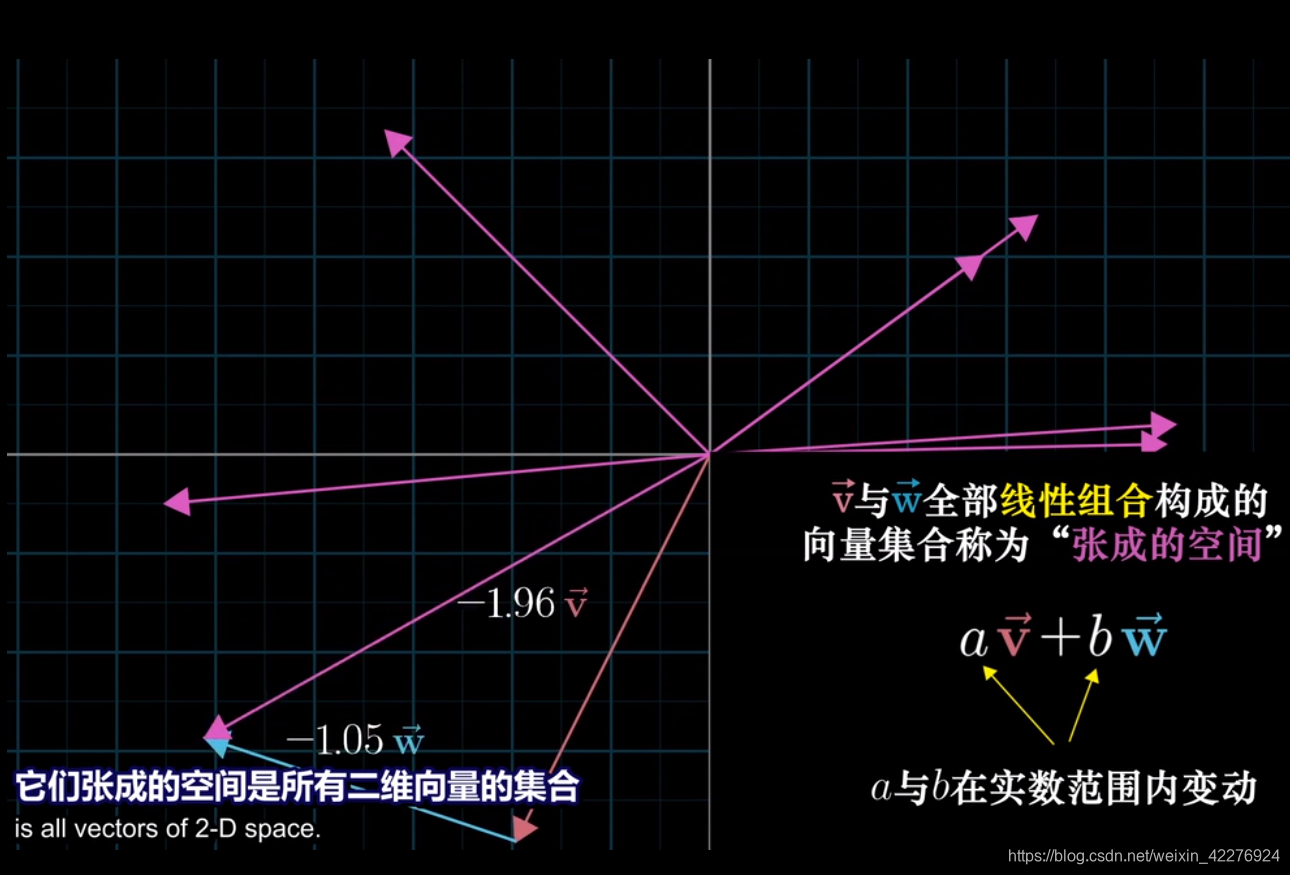
基向量的全部线性组合构成的向量集合称为“张成的空间”。(av+bw)
线性相关:一组基向量,张成一个空间o,若移除这组基向量中的一个向量i,张成的空间o不变,那么就说这组基向量是线性相关的,说被移除的向量i可以被其他的向量线性表示。理解为向量i对于空间的张成没有贡献,是多余的。
线性无关:任意一个向量都在其他向量张成的空间中,也就是对所有的a和b,u=av+bw均不成立。
4、矩阵与线性变换
线性变换,Linear Tranformation。相当于一种函数效果,接收一个向量输入,得到一个向量输出。在几何空间中的可视化表达就是原向量转动、缩放得到输出向量。而线性变换就是这个转动与缩放的过程。最终,这个过程可以通过一个矩阵来进行数值化的精确表达。
什么是线性变换?关键是线性,若不限制为线性,那么变换将会尤为复杂华丽。当限制为线性,就指定了两个规则:
a.直线变换后仍然为直线,不能弯曲。
b.远点固定不变。
总之,可以将线性变换看作一种“保持网格线平行且等距分布的变换”。
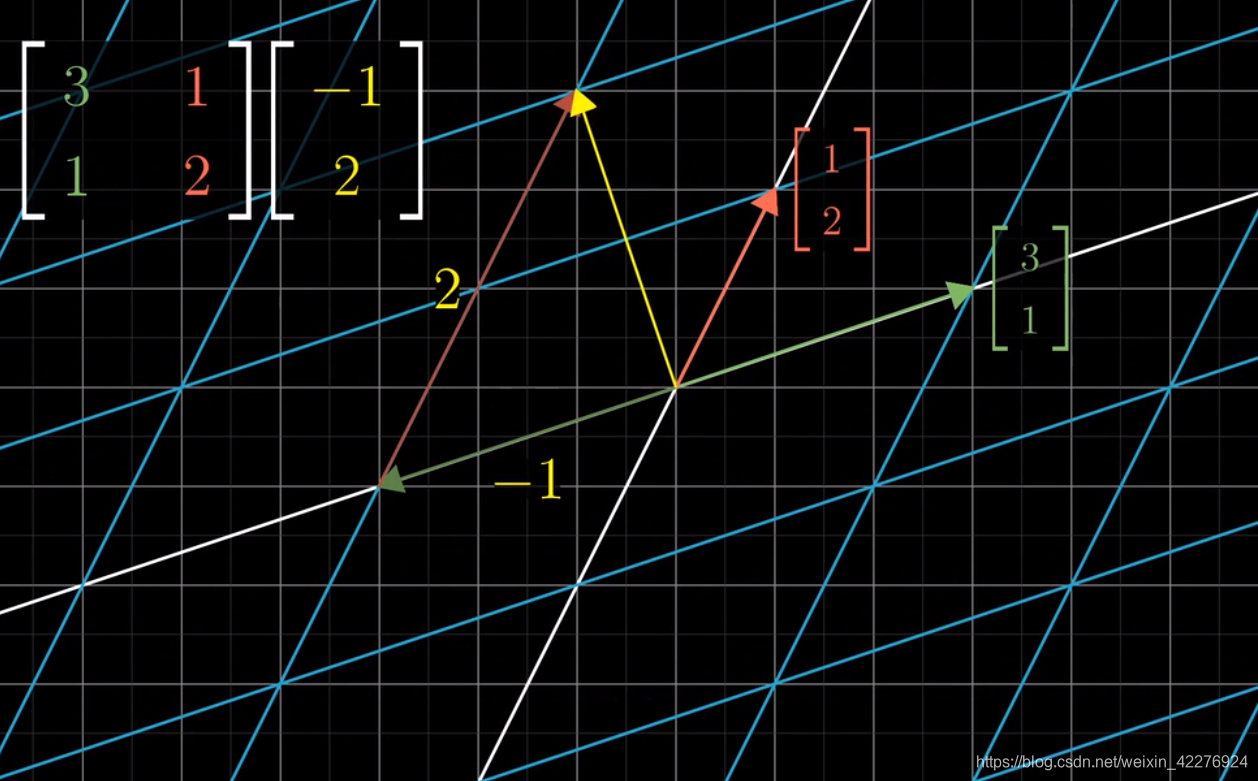
线性变换实际可以看成空间的基的变换。而其他所有向量都能用这组基线性表示,且变换前后线性表示的系数不变。即知道空间基向量变换后的坐标就能知道所有向量在这个变换作用后的情况。
矩阵:将上述空间基向量线性变换后的向量坐标用一个矩阵表示,如[x1,x2;y1,y2],它的列向量分别表示两个基向量变换后的坐标。那么任意向量与这个矩阵的乘法(二维空间内)就是这个向量在这个矩阵描述的线性变换后的向量坐标。
若线性变换后的基向量线性相关,即矩阵的列向量相关,则原空间会被挤压丢失维度。(这两个线性相关向量所张成的一维空间)
重要概念:矩阵是一种空间的线性变换,每一个列都看成原空间的一个基向量的变换后的坐标(向量)。
5、矩阵乘法与线性变换复合
两个矩阵相乘,就是两个矩阵所表示的线性变换的复合变换。M1M2
注:这种理解下,矩阵乘法的分步变换应该从右到左进行,即第二个被乘矩阵M2对应第一次线性变换,第一个乘数M1是第二次线性变换。
两个矩阵相乘的结果就是,原空间坐标系(对应为一个单位矩阵E),在这两个矩阵所代表的线性变换之后的坐标。如M1M2=M1(M2*E)。即空间的基向量组先进行M2对应的线性变换,再进行M1对应的线性变换。

6.、三维空间下的线性变换
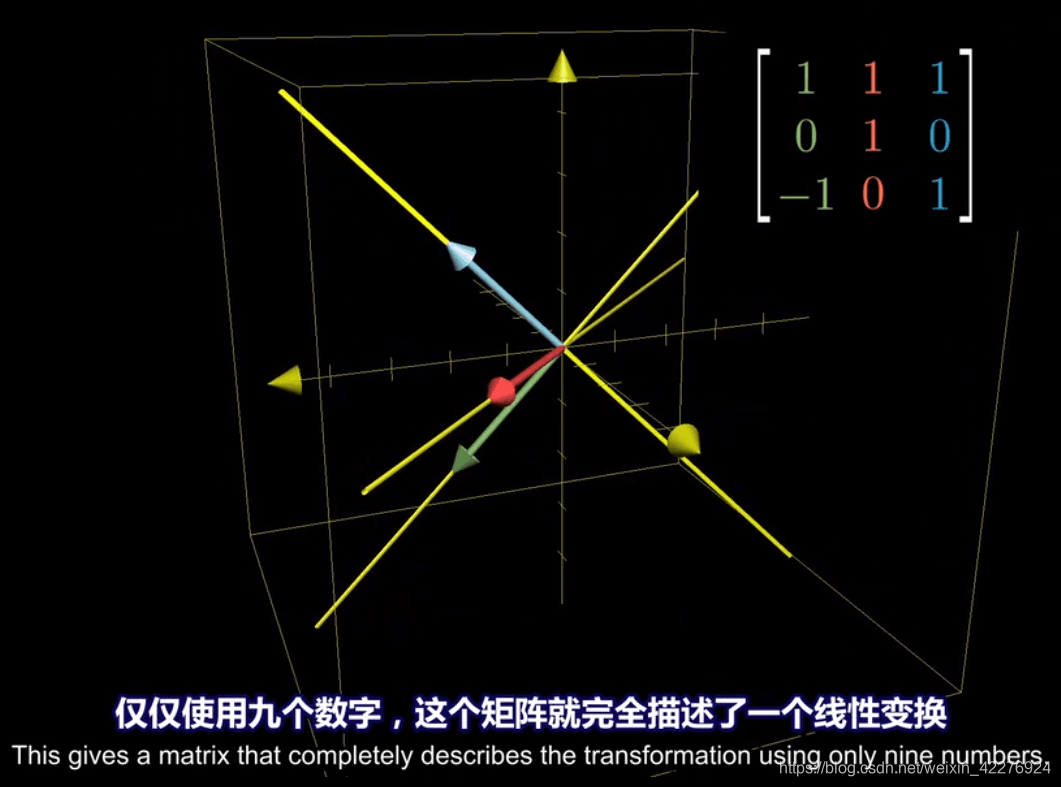
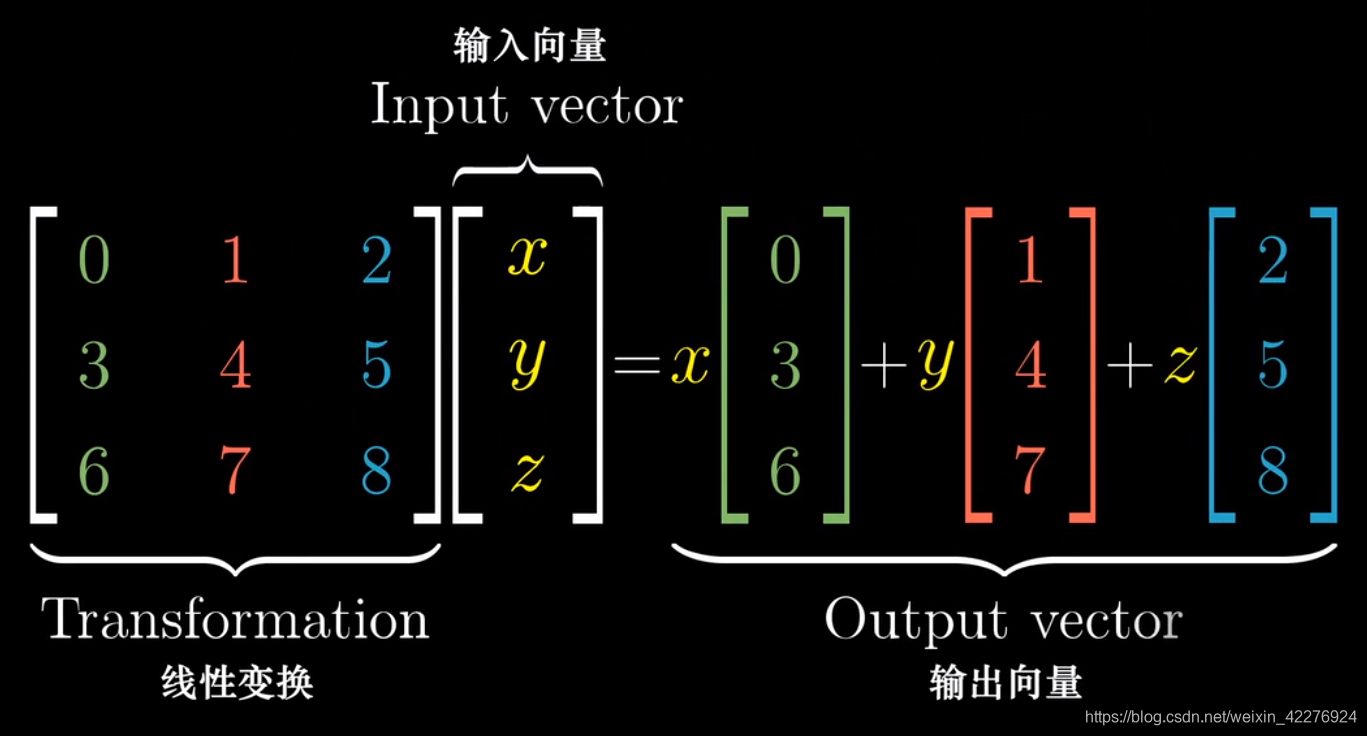





 本文探讨了线性代数的数值和几何层面,介绍了向量的定义及其在二维空间中的表示。线性组合和基向量的概念帮助理解向量空间,矩阵则作为线性变换的工具,用于描述空间中向量的旋转和缩放。矩阵乘法表示线性变换的复合,揭示了线性变换的顺序性质。最后,讨论了三维空间下的线性变换。
本文探讨了线性代数的数值和几何层面,介绍了向量的定义及其在二维空间中的表示。线性组合和基向量的概念帮助理解向量空间,矩阵则作为线性变换的工具,用于描述空间中向量的旋转和缩放。矩阵乘法表示线性变换的复合,揭示了线性变换的顺序性质。最后,讨论了三维空间下的线性变换。

















 2537
2537

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








