多段图问题
多段图问题是利用动态规划思想解决的经典问题之一,在日常生活中应用广泛。
问题描述
若存在一个有向加权图G,且G能分出起点和终点以及中间的n的阶段,求起点到终点的最短(长)距离。
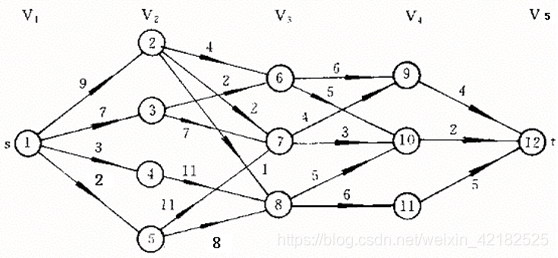
分析设计
通过上图我们可以很容易知道,如果用穷举的方法是没有办法求解的,问题规模实在太大,我们需要使用其他更为高效的算法:动态规划。
动态规划解决该问题的主要思想:n个阶段的大问题很难求解,可以将其进行划分成子问题:n-1个阶段的多段图……1个阶段的子问题容易解决,就能解决整个问题。也就是说每一个阶段都是整个问题的一个最优子结构。
如果从点s到点t的最短路径经过点vi,则vi到t也是最短距离。
构造规划方程:
fi = min{fi-1[n] + xi};
i是该段图中的点,fi 表示该点到终点的最短距离,xi表示该点到上一阶段的点的距离;
因此多段图问题的算法步骤为:
- 从最后一段算起,找出每段的每个点的最短距离;
- 每段逐一向前推,直到算至起点;
- 比较从起点到终点的距离得出最短距离。
源代码
#include <iostream>
#include <vector>
#define MAX 9999
using namespace std;
//初始化图
void initGraph(vector<vector<int> > &g, vector<vector<int> > &s) {
cout << "输入边信息:(顶点a 顶点b 权值w)(输入0结束)" << endl;
int i, j;
while (cin >> i && i) {
cin >> j;
cin >> g[i][j];
}
cout << "输入起点:";
cin >> s[1][0];
int level;
cout << "输入中间阶段数:(不含起点和终点层)";
cin >> level;
int a = 2;
for (int i = 1; i <= level; i++) { //将点分阶段
cout << "输入中间第" << i << "阶段的点:(输入0结束)";
int k, j = 0;
while (cin >> k && k) {
s[a][j++] = k;
}
a++;
}
cout << "输入终点:";
cin >> s[a][0];
}
//寻找路径
void way(vector<vector<int> > &g, vector<vector<int> > &s, vector<vector<int> > &f, vector<int> &result) {
int n = g.size() - 1; //获取结点数
int level, i; //获取总层数(包含起点终点)
for (i = 1; i <= n; i++)
if (s[i][0] == 0)
break;
level = i - 1;
int t = n;
int start = s[1][0];
int end = s[level][0];
for (i = level - 1; i >= 1; i--){ //阶段
int j = 0;
while (s[i][j]){ //该层次有点
int m = 0; //i+1阶段的点
f[i][j] = MAX;
if (g[s[i][j]][end] == MAX){
while (s[i + 1][m] != 0){
if (g[s[i][j]][s[i + 1][m]] != MAX){
if (f[i][j] > (f[i + 1][m] + g[s[i][j]][s[i + 1][m]])){
f[i][j] = f[i + 1][m] + g[s[i][j]][s[i + 1][m]];
result[s[i][j]] = s[i + 1][m];
t--;
}
}
m++;
}
}
else{
while (s[i + 1][m] != 0){
if (f[i][j] > (f[i + 1][m] + g[s[i][j]][s[i + 1][m]])){
f[i][j] = f[i + 1][m] + g[s[i][j]][s[i + 1][m]];
result[s[i][j]] = s[i + 1][m];
t--;
}
m++;
}
}
j++;
}
}
}
//打印
void print(vector<int> &result, vector<vector<int> > &s, vector<vector<int> > &f) {
int n = result.size() - 1;
cout << "最短路径为:";
int t = s[1][0];
cout << t; //起点
while (result[t] != s[n][0]) {
cout << " ->" << result[t];
t = result[t];
}
cout << endl << "最短距离为:" << f[1][0] << endl;
}
int main() {
int vexNum;
cout << "输入点的个数:";
cin >> vexNum;
vector<vector<int> > graph(vexNum + 1, vector<int>(vexNum + 1, MAX)); //保存边的长度
vector<vector<int> > s(vexNum + 1, vector<int>(vexNum + 1, 0)); //保存每个阶段的状态
vector<vector<int> > f(vexNum + 1, vector<int>(vexNum + 1, 0)); //保存该状态下点到终点的距离
vector<int > result(vexNum + 1, 0); //保存结果
initGraph(graph, s); //初始化图
way(graph, s, f, result); //寻找最短路径
print(result, s, f); //输出结果
system("pause");
return 0;
}
运行结果
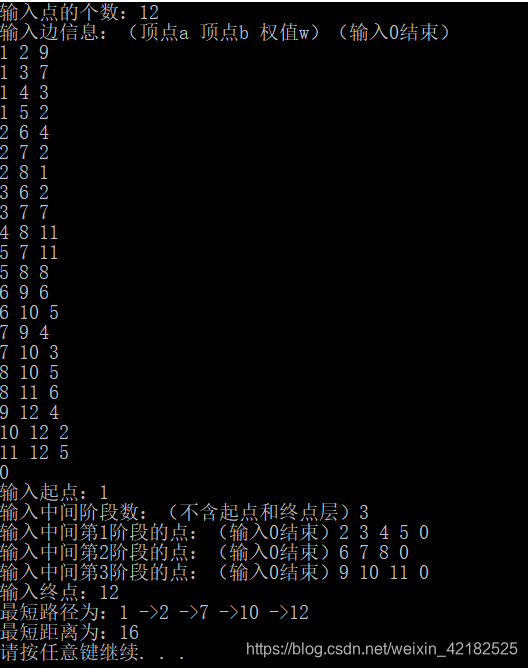











 本文介绍了如何使用动态规划解决多段图问题,详细阐述了问题描述、分析设计及算法步骤,并给出了源代码和运行结果。动态规划通过将大问题分解为子问题,逐段向前推算,找到起点到终点的最短距离。
本文介绍了如何使用动态规划解决多段图问题,详细阐述了问题描述、分析设计及算法步骤,并给出了源代码和运行结果。动态规划通过将大问题分解为子问题,逐段向前推算,找到起点到终点的最短距离。
















 929
929

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








