【概率】如何求分布函数：Z=离散X+连续Y，Y=F(X)(未完)，最大值/最小值，绝对值？同分布的含义？求抽样分布的方法？

对一些例题及细节进行了思考，整理了些思路。

目录

1. Z=离散X+连续Y

2. M=max{X, Y}，N=min{X, Y}

3. (F(x))^n 与 F(x1)……F(xn) 的区别

4. 统计量的分布（抽样分布）

---

1. Z=离散X+连续Y

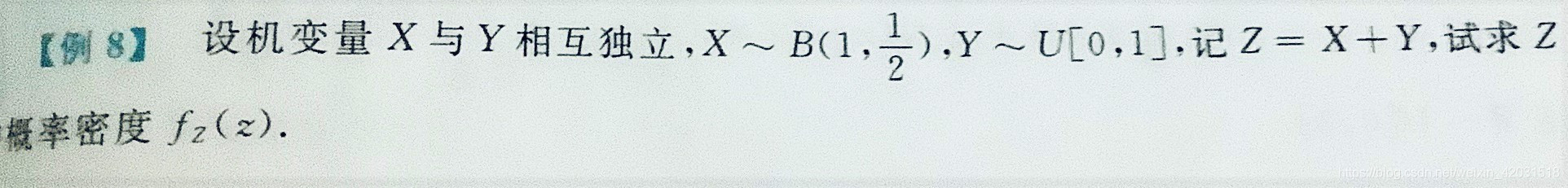
注：① 函数的表达要注意看脚标和括号。脚标指的是谁（哪个变量）对应的分布，括号内指的是把谁（哪个变量）代入这个函数。所以  指把随机变量 Z 的具体取值 z 代入随机变量 Z 对应的密度函数。 是把随机变量 Z 的取值 z 代入 Y 对应的密度函数。

② 这道题的本意是，求 Z 的密度，但是 Z 与 X、Y 有关，而 X 是 离散型变量，所以可以把 X 的各取值代入，而不必在最后 Z的密度函数中出现。这里可以看成全概率公式，在每一种 X 取值下计算并求和。所以相当于是在 X 取某些值的情况下，要把 z 代入 Y 的密度函数中，这就是题意。

③ f(z) 与 f(z-1) 在 0≤z≤2 内，取值分别是0和1，所以和始终为1。

2. Y=F(X)