堆（Heap）

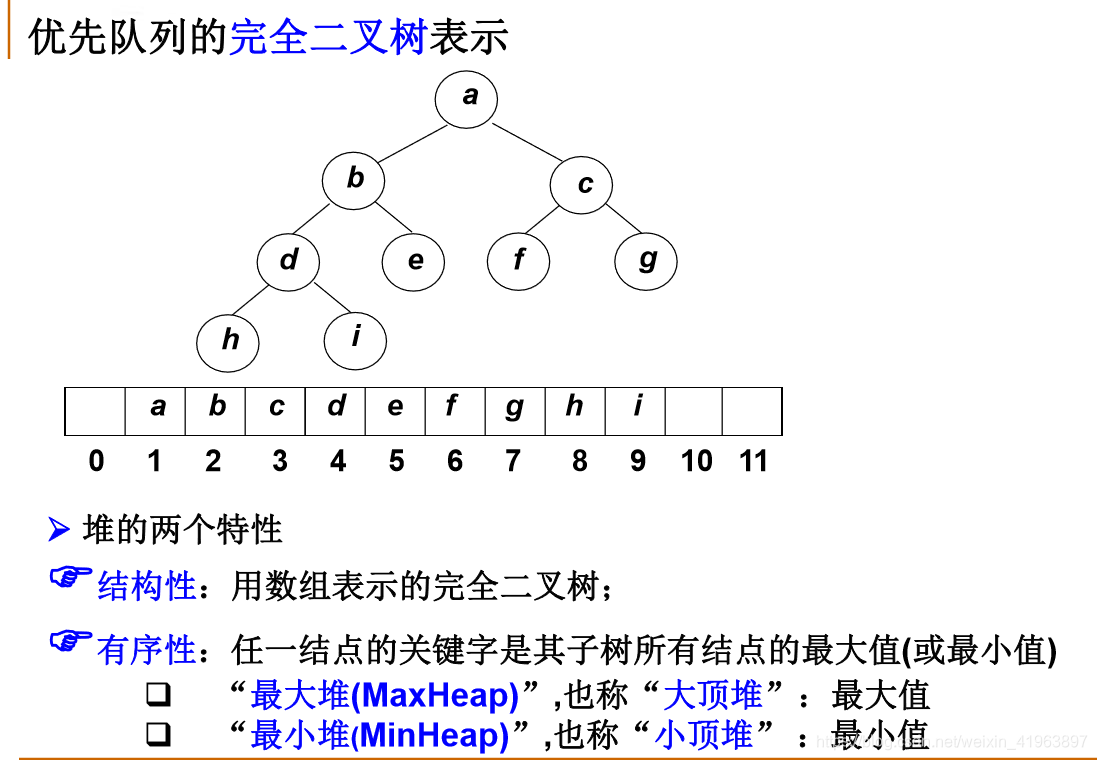
堆的定义

优先队列（Priority Queue）：特殊的“队列”，取出元素的顺序是 依照元素的优先权（关键字）大小，而不是元素进入队列的先后顺序。

堆的抽象数据类型描述

以最大堆为例
•MaxHeap Create( int MaxSize )：创建一个空的最大堆。
•Boolean IsFull( MaxHeap H )：判断最大堆H是否已满。
•Insert( MaxHeap H, ElementType item )：将元素item插入最大堆H。
•Boolean IsEmpty( MaxHeap H )：判断最大堆H是否为空。
•ElementType DeleteMax( MaxHeap H )：返回H中最大元素(高优先级)。

操作集

/*堆的结构*/
typedef struct HNode* Heap;
struct HNode{
    ElementType* Data;/*存储数据的数组*/
    int Size;/*堆中现有数据量*/
    int Capacity;/*堆容量*/
}；
/*创建最大堆*/
Heap CreateHeap(int MaxSize)
{
    Heap H;
    H=(Heap)malloc(sizeof(struct HNode);
    H->Capacity=MaxSize;
    H->Data=(ElementType*)malloc(sizeof(ElementType)*(MaxSize+1));/*0位为哨兵结点*/
    H->Size=0;
    H->Data[0]=MaxData;/*哨兵*/
    return H;
}
/*将item插入已定义哨兵的H中*/
void Insert(Heap H,ElementType item)
{
    int i;
    i=++H->Size; /*将新元素暂时放在最后*/
    for(;item>H->Data[i/2];i=i/2)/*数结点标号从1开始*/
        H->Data[i]=H->Data[i/2];/*上滤*/
    H->Data[i]=item;
}/*Insert的时间复杂度T(N)=O(logN)*/
ElementType DeleteMax(Heap H)
{
     int max=H->Data[1];
     int tmp=H->Data[H->Size--];
     int parent,child;
     for(parent=1;parent*2<=H->Size;parent=child){
          child=parent*2;
          /*不要忘记判断是否有右儿子*/
          if(child!=H->Size&&H->Data[child]<H->Data[child+1]) child++;
          if(H->Data[child]>tmp) H->Data[parent]=H->Data[child];/*下滤*/
          else break;}
    H->Data[parent]=tmp;
    return max;
} 
/*建造最大堆，对已存在数据转换*/
void percdown(Heap H，int p)
{
  /* 下滤：将H中以H->Data[p]为根的子堆调整为最大堆 */
    int tmp=H->Data[p];
    int parent,child;
    for(parent=p;parent*2<=H->Size;parent=child){
        child=parent*2;
        if(child!=H->Size&&H->Data[child]<H->Data[child+1])child++;
        if(H->Data[child]>tmp)H->Data[parent]=H->Data[child];
        else break;}
    H->Data[parent]=tmp; 
}       
void BuildHeap(Heap H)
{
    /* 调整H->Data[]中的元素，使满足最大堆的有序性  */  
    /* 这里假设所有H->Size个元素已经存在H->Data[]中 */
    int i;   
    /* 从最后一个结点的父节点开始，到根结点1 */
    for(i=H->Size/2;i>0;i--)
        percdown(H,i);
}