Acwing 788. 逆序对的数量 C++

最新推荐文章于 2024-05-07 23:07:27 发布

原创最新推荐文章于 2024-05-07 23:07:27 发布 · 345 阅读

0 ·

CC 4.0 BY-SA版权

暑假算法同时被 2 个专栏收录

127 篇文章

订阅专栏

Acwing

94 篇文章

订阅专栏

本文介绍了一种利用归并排序算法高效计算数组中逆序对数量的方法。逆序对是指数组中满足特定条件的元素对，该文详细解释了逆序对的定义，并通过归并排序算法实现逆序对的计数，最后给出具体实例和代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

给定一个长度为n的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i < j 且 a[i] > a[j]，则其为一个逆序对；否则不是。

输入格式

第一行包含整数n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

输出格式

输出一个整数，表示逆序对的个数。

数据范围

1≤n≤100000

输入样例：

6
2 3 4 5 6 1

输出样例：

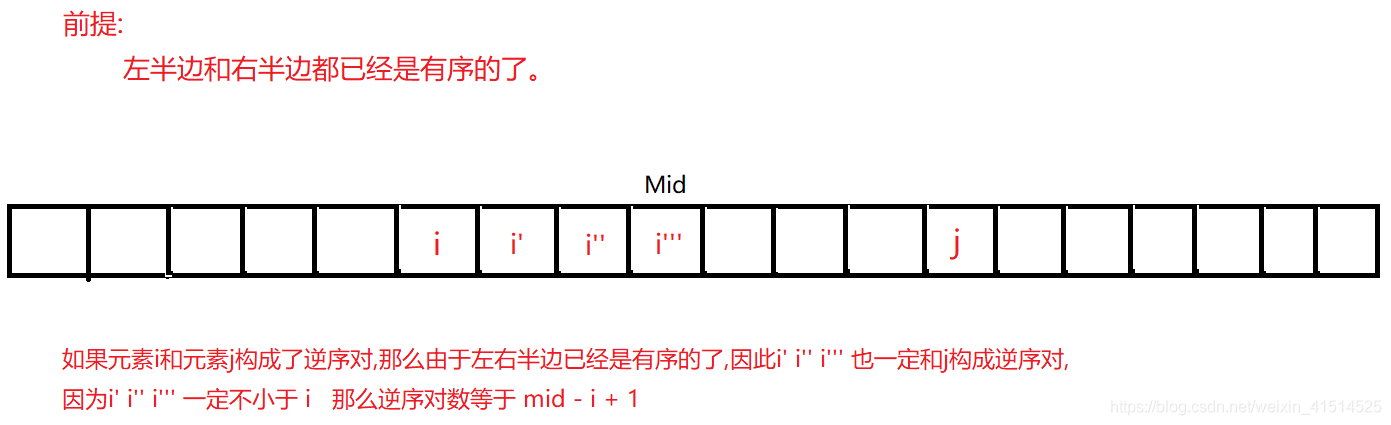
逆序对的解法是使用了归并排序的代码。 归并排序的中间值mid,逆序对的两个数出现的位置有3种，一个是都在mid的左端或者右端，或者是分别在两端。 
因此可以递归的写出[l,r]中的逆序和。

[ num1 num2 mid ]    [ mid num1 num2 ]   [ num1 mid num2 ]

# include<iostream>
using namespace std;
int res[100010],tem[100010];

int count = 0;

void merge_sort(int l,int r){  // 求区间[l,r]中的逆序对数
    if (l >= r) return 0;
    int mid = (l + r) >> 1;
    merge_sort(l,mid) + merge_sort(mid+1,r);  // 对于两个数在一边的情况递归求解
    
    int k = 0,i = l ,j = mid + 1;  // k从0开始,因为k是临时数组tmp的下标,由于tmp的任务就是临时装左右归并的结果,不是最终的数字排序结果数组,只需要从1开始就可以了。
    
    while(i <= mid && j <= r){
        if (res[i] <= res[j]){
            tem[k++] = res[i++];
        }else{
            count += mid - i + 1;  // 如果左边[l,mid]区间中res[i]比右边区间[mid+1,r]中的res[j]大的话，那么在左边区间[i+1,mid]中的数都和res[j]构成了逆序对(因为上面先对左右半边进行了归并，现在左右半边各自都是有序的)，一共mid-i+1个
            tem[k++] = res[j++];
        }
    }
    
    while(i<=mid) tem[k++] = res[i++];
    while(j<=r) tem[k++] = res[j++];
    
    for (int i = l,j = 0; i <= r;i++,j++) res[i] = tem[j];
}

int main(){
    int n;
    scanf("%d",&n);
    for (int i = 0; i < n ;i++){
        scanf("%d",&res[i]);
    }
    cout<<merge_sort(0,n-1);
    return 0;
}