VAE全面理解（下）

在上一篇中，我自认为用浅显的语言向诸位介绍了VAE的整个发展的过程，在这篇中，将较多的涉及框架构建以及公式推导部分。

那么，开始吧

1）框架构建

首先我们有一批数据样本 x1,…,xn}，其整体用 X 来描述，我们本想根据 {x1,…,xn} 得到 X 的分布 p(X)，如果能得到的话，那我直接根据 p(X) 来采样，就可以得到所有可能的 X 了（包括 {x1,…,xn} 以外的），这是一个终极理想的生成模型了。但是，这个过程往往是很困难的。

于是，我们退而求其次，就想到了上文中提到的隐形变量Z，这个Z就是决定最终x形态的因素向量。给定一个图片Xk，我们假定p(Z|Xk)是专属于Xk的后验概率分布，这个概率分布服从正态分布。得到了这个概率，我们可以从分布中采样，并且通过最终的解码器将图片再恢复出来。

由于上述所说，我们所假设的这些分布都是正态分布，那么我们就需要求得相应的方差和均值，所以在编码实现的过程中，不难看到encoder部分真实做的事情就是，对相应的输入数据，通过两个网络产生了均值和方差。

那么，我们再次思考一下接下来的训练过程，我们的目的是使重构之后的图片与输入的图片之间的差距越小越好。但是在这重构在引入均值方差以及之后的高斯分布的时候，是引入了噪声的，也就是说为了提高模型的准确性，这个高斯分布的方差最后将收敛为零，而在这个时候，模型也就失去了生成的效果，无法生成新的图片。

那怎么办呢，别急，还记得之前VAE的一个假设嘛？p(Z|Xk)是服从高斯分布的。所以，通过下面这个公式的计算，我们可以求得Z的分布：

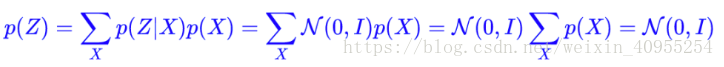
这样的话，Z的分布就会保持在标准正态分布，从而保证了生成器可以继续生