轨迹的多项式拟合简介

火山大兄

已于 2024-08-05 13:30:39 修改

阅读量1.2k

点赞数 17

分类专栏：无人驾驶车辆文章标签：自动驾驶

于 2024-07-23 15:50:18 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_40240807/article/details/140627604

版权

无人驾驶车辆专栏收录该内容

15 篇文章

订阅专栏

自动驾驶运动规划中会用到各种曲线，主要用于生成车辆的轨迹，常见的轨迹生成算法，如贝塞尔曲线，样条曲线，以及apollo EM Planner的五次多项式曲线。城市场景中使用的是分段多项式曲线，在EM Planner和Lattice Planner中思路是，都是先通过动态规划生成点，再用5次多项式生成曲线连接两个点（虽然后面的版本改动很大，至少Lattice planner目前还是这个方法）。

在这里可以看出5次多项式的作用，就是生成轨迹。这里的轨迹不一定是车行驶的轨迹，比如S—T图中的线，是用来做速度规划的。如下图：

在Apollo里面用到了3-5次多项式：cubic_polynomial_curve1d（三次多项式曲线）、quartic_polynomial_curve1d（四次多项式曲线）和quintic_polynomial_curve1d（五次多项式曲）线。在此我们介绍下五次多项式在横向规划下的使用。

$d(t) = c_{0}+c_{1}t^{1}+c_{2}t^{2}+c_{3}t^{3}+c_{4}t^{4}+c_{5}t^{5}$

其中，t代表时间，d代表S-L坐标系下的横向偏差。因为是使用多项式连接两个已知点，所以两个轨迹点的信息是已知的。假设起始的t=0时刻，横向位置 $d_{0}$ ，横向车速 $\dot{d}_{0}$ ，横向加速度 $\ddot{d}_{0}$ ，t=tp时刻，横向位置 $d_{p}$ ，横向车速 $\dot{d}_{p}$ ，横向加速度 $\ddot{d}_{p}$ （通常我们认为应该是跟踪轨迹稳定行驶，即横向车速 $\dot{d}_{p}$ 和横向加速度 $\ddot{d}_{p}$ 均为0），则对公式求导得：

$\dot{d}(t) = c_{1}+2c_{2}t^{1}+3c_{3}t^{2}+4c_{4}t^{3}+5c_{5}t^{4}$

$\ddot{d}(t) =2c_{2}+6c_{3}t^{1}+12c_{4}t^{2}+20c_{5}t^{3}$

则有：

$d_{0}=c_{0}$

$\dot{d}_{0}=c_{1}$

$\ddot{d}_{0}=2c_{2}$

$d_{p}= c_{0}+c_{1}t_{p}^{1}+c_{2}t_{p}^{2}+c_{3}t_{p}^{3}+c_{4}t_{p}^{4}+c_{5}t_{p}^{5}$

$\dot{d}_{p} = c_{1}+2c_{2}t_{p}^{1}+3c_{3}t_{p}^{2}+4c_{4}t_{p}^{3}+5c_{5}t_{p}^{4}$

$\ddot{d}_{p} =2c_{2}+6c_{3}t_{p}^{1}+12c_{4}t_{p}^{2}+20c_{5}t_{p}^{3}$

六个变量六个方程因此可以求解得出：

$c_{0} = d_{0}$

$c_{1} = \dot{d}_{0}$

$c_{2}=\ddot{d}_{0}/2$

$c_{3}=(-20d_{0}+20d_{p}-12\dot{d}_{0}t_{p}-8\dot{d}_{p}t_{p}-3\ddot{d}_{0}t_{p}^{2}+\ddot{d}_{p}t_{p}^2)/2*t_{p}^3$

$c_{4}=(30d_{0}-30d_{p}+16\dot{d}_{0}t_{p}+14\dot{d}_{p}t_{p}+3\ddot{d}_{0}t_{p}^{2}-2\ddot{d}_{p}t_{p}^2)/2*t_{p}^4$

$c_{5}=(-12d_{0}+12d_{p}-6\dot{d}_{0}t_{p}-6\dot{d}_{p}t_{p}-\ddot{d}_{0}t_{p}^{2}+\ddot{d}_{p}t_{p}^2)/2*t_{p}^5$

公式的计算结果可使用matlab来处理。具体参考：MATLAB求解多元一次方程组-优快云博客。

关于t=tp时刻的横向位置 $d_{p}$ ，横向车速 $\dot{d}_{p}$ ，横向加速度 $\ddot{d}_{p}$ ，可以按照横向位置和到达时间对终点进行多组的采样。

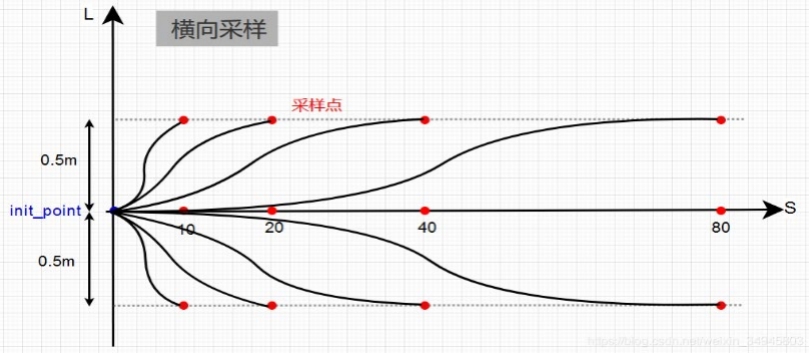
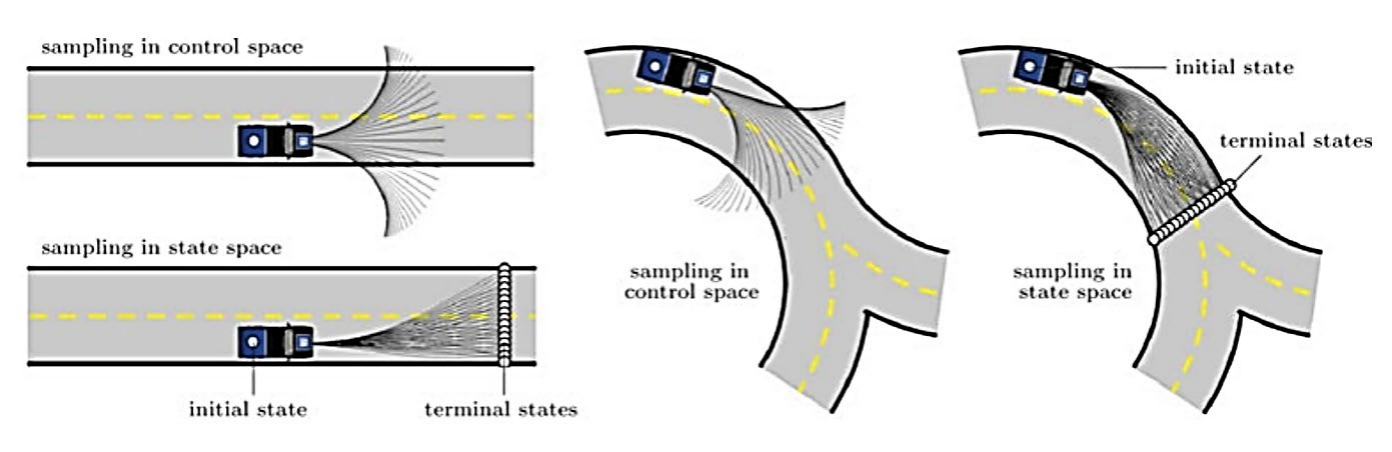假设横向的范围d∈[-4,4]，时间范围t∈[4,12]。在t=0时刻的状态为[0,0,0]（初始位置，无横向速度，无横向加速度），t=tp时刻的状态为[d,0,0]（横向d位置，无横向速度，无横向加速度）。使用MATLAB回执多项式的拟合曲线的脚本：

clc;
clear;
close;

figure(1)
hold on
for p = -4:1:4
    for t = 4:4:12
        c = polynomial(0,0,0,p,0,0,t);
    end
end

function c = polynomial(x0,dx0,ddx0,xp,dxp,ddxp,tp)
    c = zeros(1,6);
    syms c0 c1 c2 c3 c4 c5 
    % 定义一次方程
    eq1 = c0 == x0;
    eq2 = c1 == dx0;
    eq3 = 2*c2 == ddx0;
    eq4 = c0 + c1*tp + c2*tp^2 + c3*tp^3 + c4*tp^4 + c5*tp^5 == xp;
    eq5 = c1 + 2*c2*tp + 3*c3*tp^2 + 4*c4*tp^3 + 5*c5*tp^4 == dxp;
    eq6 = 2*c2 + 6*c3*tp + 12*c4*tp^2 + 20*c5*tp^3 == ddxp;
    % 解方程组
    sol = solve([eq1, eq2, eq3, eq4, eq5, eq6], [c0,c1,c2,c3,c4,c5]);
    % 
    c(1) = sol.c0;
    c(2) = sol.c1;
    c(3) = sol.c2;
    c(4) = sol.c3;
    c(5) = sol.c4;
    c(6) = sol.c5;
    %
    c0 = c(1);
    c1 = c(2);
    c2 = c(3);
    c3 = c(4);
    c4 = c(5);
    c5 = c(6);
    accuracy = 0.1;
    n = tp / accuracy + 1;
    arr = zeros(n,2);
    for i = 0:n-1
        t = i*accuracy;
        arr(i+1,1) = t;
        arr(i+1,2) = (((((c5*t)+c4)*t+c3)*t+c2)*t+c1)*t+c0;
    end
    plot(arr(:,1),arr(:,2),'r-',LineWidth=2);
end

除此之外，还可以用矩阵求逆的方式来求解：

可以看成矩阵：

$Ac=B$

则

$c=A^{-1}B$

可以用：Eigen::Vector3f c = A.colPivHouseholderQr().solve(B)求解。缺点是可能比较耗时。

  // polynomial parameters
  QuinticPolynomial(float xs_, float vxs_, float axs_, float xe_, float vxe_,
                    float axe_, float T)
      : xs(xs_),
        vxs(vxs_),
        axs(axs_),
        xe(xe_),
        vxe(vxe_),
        axe(axe_),
        a0(xs_),
        a1(vxs_),
        a2(axs_ / 2.0) {
    Eigen::Matrix3f A;
    A << std::pow(T, 3), std::pow(T, 4), std::pow(T, 5), 3 * std::pow(T, 2),
        4 * std::pow(T, 3), 5 * std::pow(T, 4), 6 * T, 12 * std::pow(T, 2),
        20 * std::pow(T, 3);
    Eigen::Vector3f B;
    B << xe - a0 - a1 * T - a2 * std::pow(T, 2), vxe - a1 - 2 * a2 * T,
        axe - 2 * a2;

    Eigen::Vector3f c_eigen = A.colPivHouseholderQr().solve(B);
    a3 = c_eigen[0];
    a4 = c_eigen[1];
    a5 = c_eigen[2];
  };

参考链接：

（1）自动驾驶规划 - 5次多项式拟合_五次多项式拟合-优快云博客

（2）Eigen矩阵colPivHouseholderQr().solve()求解Ax=b-优快云博客