本文深入探讨了邻近算子的概念、存在性和唯一性，通过多个实例解析其计算过程，并揭示了邻近算子与正交投影之间的紧密联系。此外，还详细阐述了指示函数的邻近算子即正交投影，以及相关的投影定理。最后，通过Moreau分解和Moreau包络，进一步解释了闭凸函数中邻近算子的特性。
本篇blog主要介绍了临近算子、临近算子与正交投影的联系、几个临近定理、Moreau分解等等
目录
1 Definition, Existence, and Uniqueness（什么是邻近算子、第一临近定理：临近算子解集只有一个元素 singleton、6.4 闭和coerciveness条件下邻近算子解集的非空性）
2 First Set of Examples of Proximal Mappings（临近算子的例子）（几种常见邻近算子的计算）
3 Prox Calculus Rules（临近算子的计算规则）（邻近算子的运算规则）
4 Prox of Indicators—Orthogonal Projections（指示函数的临近算子-正交投影）
4.1 The First Projection Theorem（也是singleton，其实可以引用第一临近定理证明，正交投影就是指数函数的临近）
4.3 Projection onto the Intersection of a Hyperplane and a Box
4.4 Projection onto Level Sets
5 The Second Prox Theorem（重点 3条等价性质 利用费马最优性条件）
(第二投影定理与第二临近定理的第3条、邻近算子的非扩张性 联想到投影算子的非扩张性)
6 Moreau Decomposition（利用第二临近定理和共轭次梯度定理证明）（增广意义下的）
7 The Moreau Envelope（Moreau包络）
7.1 Definition and Basic Properties
7.2 Differentiability of the Moreau Envelope
7.3 Prox of the Moreau Envelope
8 Miscellaneous Prox Computations
1 Definition, Existence, and Uniqueness
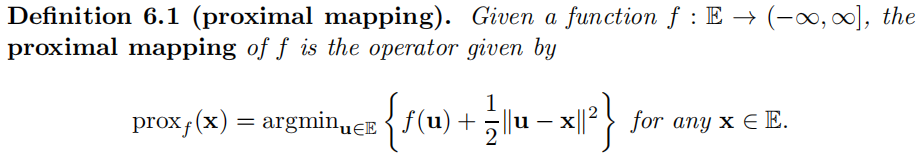
f proper , closed , convex
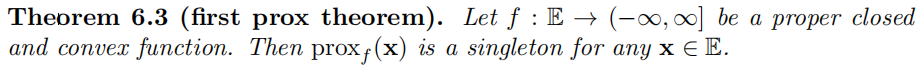
2 First Set of Examples of Proximal Mappings（临近算子的例子）
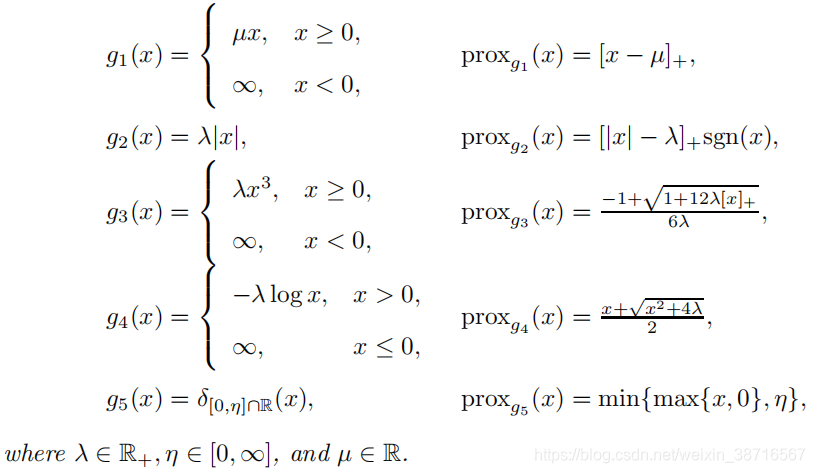
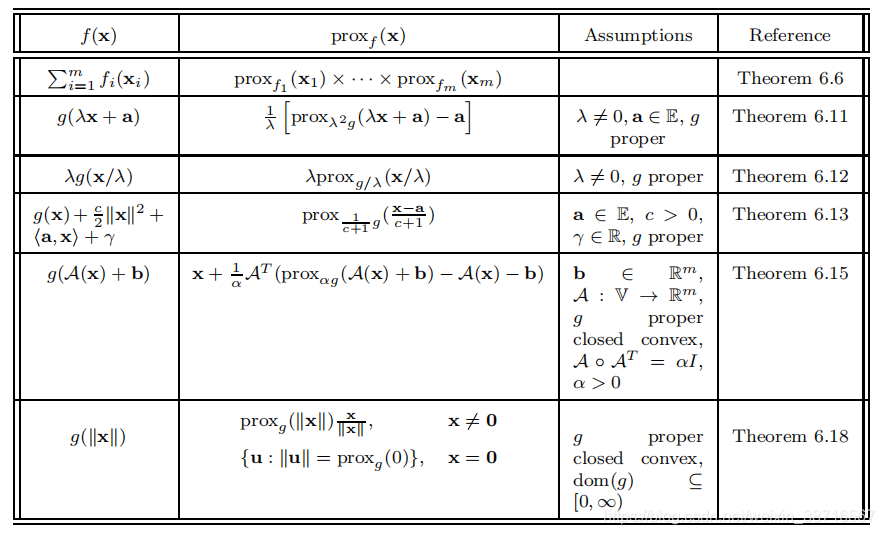
3 Prox Calculus Rules（临近算子的计算规则）
可分函数：(x又是向量)
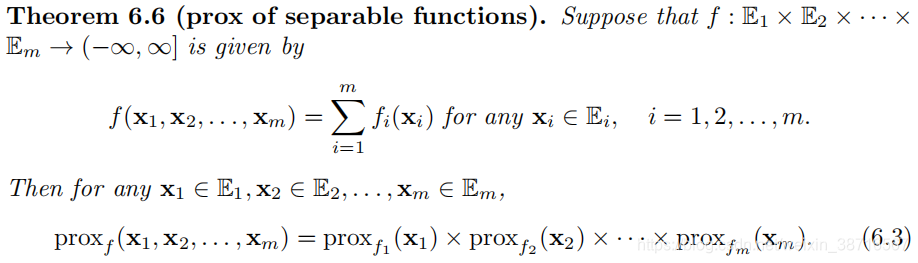
f 的缩放与平移（仅要求proper）
f proper，closed，convex
4 Prox of Indicators—Orthogonal Projections（指示函数的临近算子-正交投影）
4.1 The First Projection Theorem
正交投影算子：
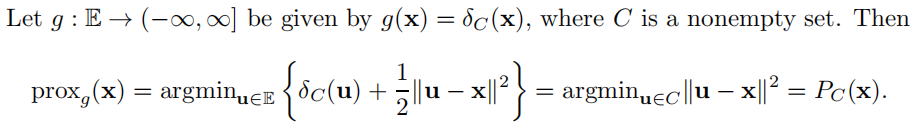
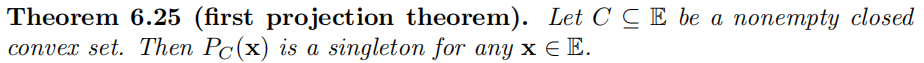
The first projection theorem:the orthogonal projection mapping (which coincides with the proximal mapping)exists and is unique.
正交投影映射与邻近映射一致
4.2 First Examples in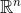 
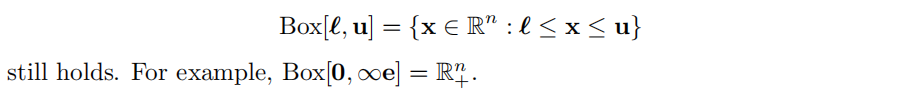
4.3 Projection onto the Intersection of a Hyperplane and a Box
4.4 Projection onto Level Sets
4.5 Projection onto Epigraphs
4.6 总结
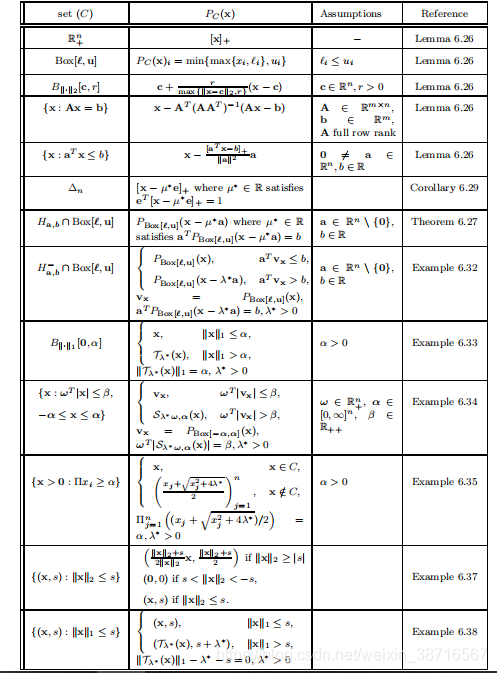
5 The Second Prox Theorem
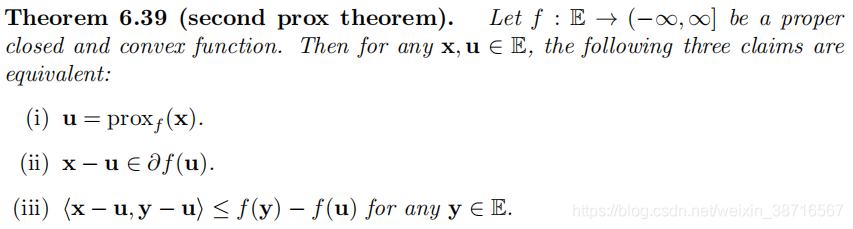
证明利用到如下Fermat最优化条件
第二投影定理：
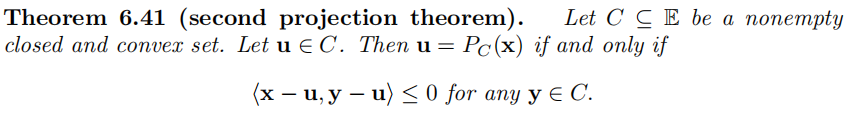
临近梯度算子的稳定非扩张性：
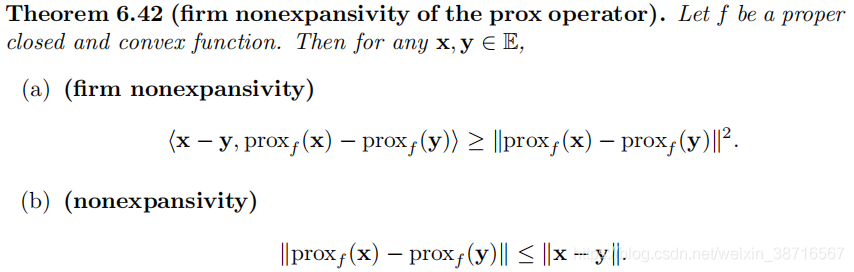
6 Moreau Decomposition
闭凸函数中的prox算子与其共轭联系起来
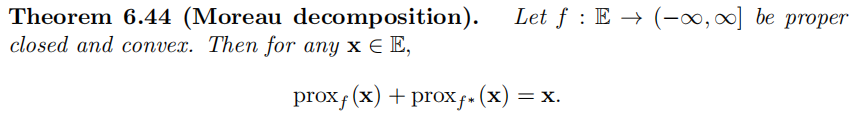
由如下共轭次梯度定理推导
增广的Moreau分解：
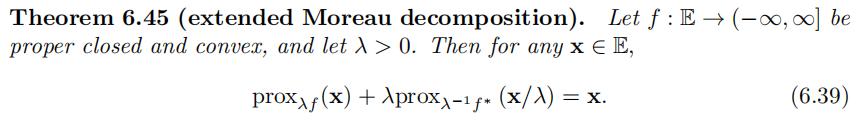
6.1 Support Functions
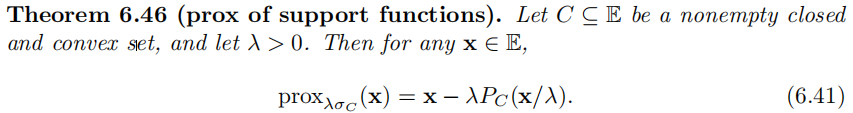
7 The Moreau Envelope（Moreau包络）
7.1 Definition and Basic Properties
μ is called the smoothing parameter.
上式由于第一临近定理，是有唯一解的，可得如下结论：
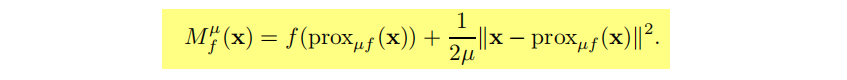
7.2 Differentiability of the Moreau Envelope
7.3 Prox of the Moreau Envelope
8 Miscellaneous Prox Computations
扫一扫
8444
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
