参考文献:first-order methods in optimization: Amir Beck
目录
1 From Gradient Descent to Subgradient Descent
2 The Projected Subgradient Method
2.2 Convergence under Polyak's Stepsize Rule
2.3 The Convex Feasibility Problem
2.4 Projected Subgradient with Dynamic Stepsizes
3 The Stochastic Projected Subgradient Method
4 The Incremental Projected Subgradient Method
5 The Dual Projected Subgradient Method
1 From Gradient Descent to Subgradient Descent
1.1 Descent Directions?
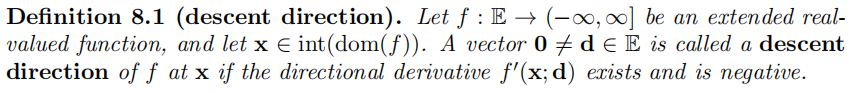
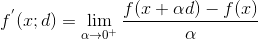 可以看出方向导数为负时,必为下降方向。
可以看出方向导数为负时,必为下降方向。
在数值优化中时,d为下降方向。
若f不可微,在非光滑的情况下,用次梯度代替梯度
![]()
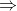
![]()
梯度方法与次梯度方法的区别在于,次梯度方向不一定是下降方向。
2 The Projected Subgradient Method
2.1 The Method


至此了解到投影次梯度的算法框架,我们只能得到上述不等式,并不能保证所有投影次梯度的收敛性,下面我们将讨论在某种步长构造下,此方法是收敛的。
2.2 Convergence under Polyak's Stepsize Rule
首先假设函数和定义域满足以下假设:

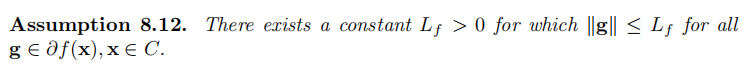
Polyak's stepsize:
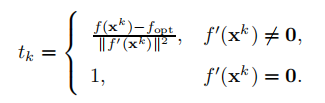
时我们可以知道
就是最优点(Remark8.10),所以对于迭代公式
,后半部分恒为0,所以此时
取值并不影响,可以任取,这里我们取1.下面我们证其收敛性。

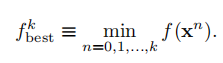
易证。值得注意的:这里xk-x*并未趋于0,并不能直接证明解的收敛,也不能说明收敛速度。证明中利用的bound可以做以下替代
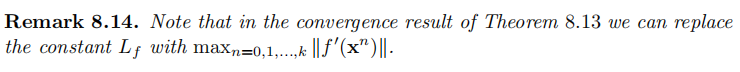
定理8.13(a)的序列性质被称为Fej´er monotonicity,我们可以证明有这种性质的序列的收敛性。
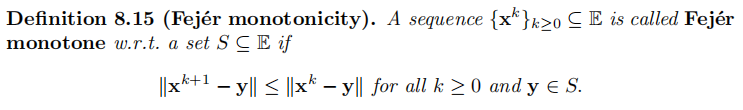
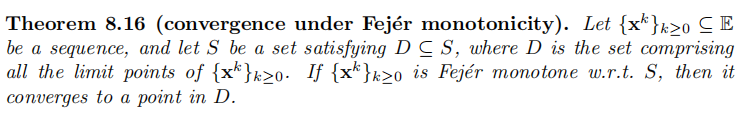
由此

由8.13(a)可知,迭代公式得到的序列都有fejer单调性,因此由8.16可知,只需证明一个极限点在中,那么其他极限点必然在
中。令x0是序列的一个极限点,那么存在序列的子列收敛于x0,且由于C的闭性,x0属于C。8.13(b)有值的收敛,由f的连续性,我们可以得到
,这意味着x0也属于最优解集。这里我们已经成功证明红字部分,这个收敛点也是一个最优解,属于X*。

有类似8.13(a)的式子出现应该都要用到这一套路。
8.13(c)体现了值有
收敛速率。
2.3 The Convex Feasibility Problem
2.4 Projected Subgradient with Dynamic Stepsizes
之前Polyak的步长需要提前知道最优值,显然无法计算。我们本节构造新的步长,依然保有的收敛率,并且发现保证
的步长构造条件。首先介绍一个引理:

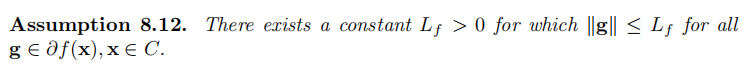

易证。讨论能使投影次梯度方法收敛的步长条件:

易证。通过8.25我们构造如下步长:

易证。说明了在这种构造下值和
有
的收敛率。我们仍然希望得到如Polyak步长下
的
的收敛速度,只需在上述构造条件中加入 C为紧集即可,重新表述:
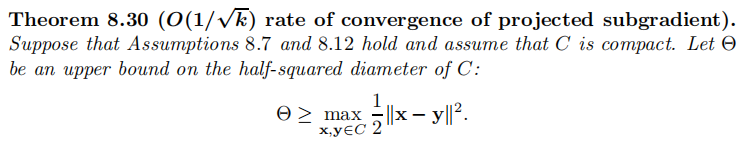

2.5 The Strongly Convex Case

3 The Stochastic Projected Subgradient Method
通过对次梯度取估计

4 The Incremental Projected Subgradient Method
对于特殊形式的问题
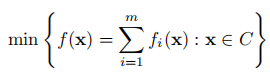

注意符号,每一小步走小函数的次梯度方向,m步就为一大步;在此特殊形势下,f分量的次梯度之和也是f的次梯度。
证明此算法在步长条件下 收敛,在C为紧时,有
的收敛速度.

5 The Dual Projected Subgradient Method
问题形式与假设:

注意强对偶条件。给出算法流程:

收敛性分析 对具体线性规划等例子的计算








 本文深入探讨了优化算法从梯度下降到次梯度下降的演变,解析了投影次梯度法及其在不同条件下的收敛性,包括Polyak步长规则、动态步长选择、随机、增量及对偶投影次梯度方法。特别强调了在特定步长构造下,算法的收敛性和收敛速度。
本文深入探讨了优化算法从梯度下降到次梯度下降的演变,解析了投影次梯度法及其在不同条件下的收敛性,包括Polyak步长规则、动态步长选择、随机、增量及对偶投影次梯度方法。特别强调了在特定步长构造下,算法的收敛性和收敛速度。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








