2019.02.25
【
- 拟牛顿方法近似hessian阵,而非精确牛顿方法某种意义上是对牛顿步p的近似
- 拟牛顿得到的近似hessian阵一般是稠密的,在大规模问题中,即使是稀疏的,也要花很大的存储,两者并不冲突;L-BFGS是对原始方法的一种减小存储量的改造,采用对此步最近的m步的
的存储,来随时计算第k步的
- 结合线搜索的非精确牛顿法/结合信赖域的非精确牛顿法
】
1 Inexact Newton Methods
牛顿方法![]() 要求Hession阵的逆,计算量大。CG、Lanczos方法;线搜索、TR搜索方法。
要求Hession阵的逆,计算量大。CG、Lanczos方法;线搜索、TR搜索方法。
在线搜索和信赖域框架下,非精确牛顿法是否能保持和牛顿法一样的收敛性;非精确,顾名思义,就是与真正的牛顿步有一定差距,那这种差距满足何种条件才能保证收敛性呢?我们在以下记此差距为$r_k$.
LOCAL CONVERGENCE OF INEXACT NEWTON METHODS
迭代的终止条件一般与残差有关,残差满足一定条件则收敛,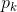 是非精确牛顿步长:
是非精确牛顿步长: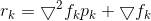 ,且
,且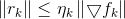
其中,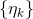 (
(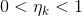 )是forcing sequence,
)是forcing sequence,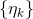 的选择决定了收敛速率。
的选择决定了收敛速率。
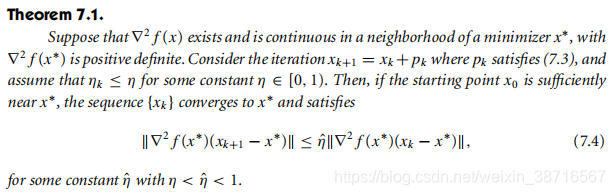
进一步地

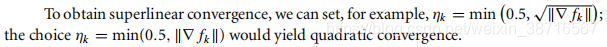
以上讨论了满足误差在某序列控制下,非精确线搜索的局部收敛性及一般情况下梯度的收敛速度;但如何在具体算法中,使误差来满足这样的条件从而确保收敛呢?我们介绍LSN-CG和TRN-CG两种具体算法。
LINE SEARCH NEWTON–CG METHOD

当Hession阵奇异是,该方向的性质不好
![]()
The line search Newton–CG method does not require explicit knowledge of the Hessian . Rather, it requires only that we can supply Hessian–vector products of the form 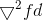 for any given vector d.
for any given vector d.
内迭代中用CG方法来计算每次的方向,然后再用线搜素方法选择步长完成一次迭代;与线搜素CG方法不同的是,他在计算方向的时候允许跟真实牛顿方向有误差。
TRUST-REGION NEWTON–CG METHOD
多了信赖域的约束

PRECONDITIONING THE TRUST-REGION NEWTON–CG METHOD
预条件处理使得特征值分布更加有利与计算
TRUST-REGION NEWTON–LANCZOS METHOD
A limitation of Algorithm 7.2 is that it accepts any direction of negative curvature, even when this direction gives an insignificant reduction in the model.
2 Limited-Memory Quasi-Newton Methods
Instead of storing fully dense n × n approximations, they save only a few vectors of length n that represent the approximations implicitly. Despite these modest storage requirements, they often yield an acceptable (albeit linear) rate of convergence.
L-BFGS算法 基于BFGS
前m步高效计算
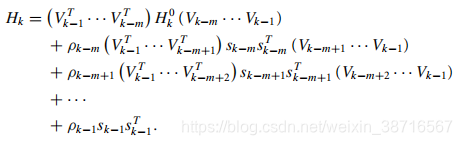


初始值的设定如下比较有效:
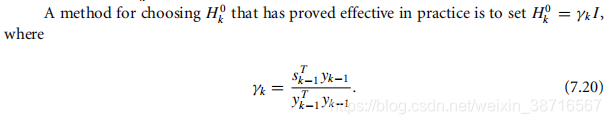

3 Sparse Quasi-Newton Updates
![]()
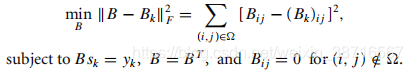
4 Algorithms for Partially Separable Functions
函数可分:
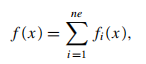
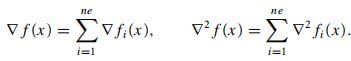





 本文探讨了非精确牛顿法在大规模优化问题中的应用,包括线搜索与信赖域方法下的收敛性,以及如何通过LSN-CG和TRN-CG算法确保误差满足收敛条件。同时,介绍了有限内存拟牛顿法,如L-BFGS算法,其在存储效率与收敛速度之间的平衡。
本文探讨了非精确牛顿法在大规模优化问题中的应用,包括线搜索与信赖域方法下的收敛性,以及如何通过LSN-CG和TRN-CG算法确保误差满足收敛条件。同时,介绍了有限内存拟牛顿法,如L-BFGS算法,其在存储效率与收敛速度之间的平衡。
















 5143
5143

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








