参考文献:first-order methods in optimization: Amir Beck
1 Vector Spaces
1.1-1.4 基本空间、维数、范数、内积的概念
1.5 凸集、仿射集的定义【凸集分离定理】
1.6 内积诱导的欧几里得范数
1.7 R^n空间:主要是向量的p范数和无穷范数
1.8 R^mn空间:矩阵的范数 F范数 ab范数 2(谱)范数 1范数 无穷范数 【谱范数EVD SVD、1 无穷范数的定义】
1.11 对偶空间 对偶范数【2范数的对偶范数】
1.5 Affine Sets and Convex Sets
- affine set:
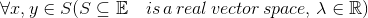 ,
, 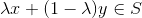 holds.
holds. - aff(S): for a set
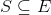 , aff(S) is the intersection of affine sets containing S.Clearly, it is the smallest affine set that containing S.
, aff(S) is the intersection of affine sets containing S.Clearly, it is the smallest affine set that containing S. - hypeplane:
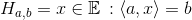 ,
,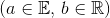
- half-spaces:
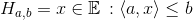 ,
,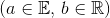
1.7 The Space 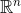
- Q-inner product :
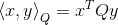
- norm of vector: p-范数:
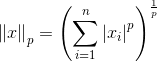
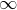 -范数:
-范数: 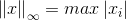
- norm of martix: 列范数:
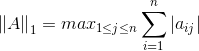 行范数:
行范数: 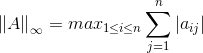 2-范数:
2-范数: 21-范数:
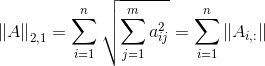 (每行2-范数求和)
(每行2-范数求和)
1.7.1 Subsets of 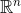 (注)
(注)
- nongegative orthant:
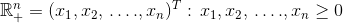 (向量元素都大于等于0的)
(向量元素都大于等于0的) - positive orthant:
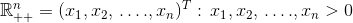 (向量元素都大于0的)
(向量元素都大于0的) - unit simplex:
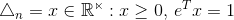 (向量元素都大于等于0的且和为1的)
(向量元素都大于等于0的且和为1的)
1.8 The Space 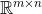
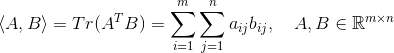
1.8.2 Norms in 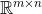
- Frobenius norm:
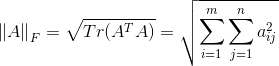
- (a, b)-norm:
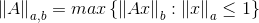
1.10 Linear Transforamtions
- linear-transformation:
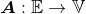
1.11 The Dual Space
- linear functional:
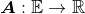
- dual space
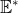 : all linear functional on
: all linear functional on 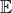
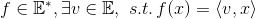
- dual norm:
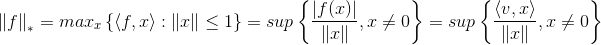
- generalized Cauchy-Schwars inequlity:
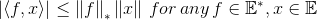
- 向量范数对偶:需满足
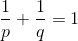 ,如 1与
,如 1与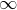 范数,2范数本身
范数,2范数本身 - 矩阵范数对偶:谱范数-核范数(特征值之和)
1.13 Adjoint Transformations
1.14 Norms of Linear Transformation
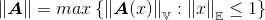





 本文深入探讨了优化领域的核心概念,包括向量空间、范数、内积、凸集及矩阵范数等,详解了R^n与R^mn空间中各种范数的定义与应用,以及对偶空间和对偶范数的原理。
本文深入探讨了优化领域的核心概念,包括向量空间、范数、内积、凸集及矩阵范数等,详解了R^n与R^mn空间中各种范数的定义与应用,以及对偶空间和对偶范数的原理。
















 981
981

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








