HoudiniVex笔记_P12_VectorBasics向量基础

原视频：https://www.youtube.com/playlist?list=PLzRzqTjuGIDhiXsP0hN3qBxAZ6lkVfGDI
Bili：Houdini最强VEX算法教程 - VEX for Algorithmic Design_哔哩哔哩_bilibili

Houdini版本：19.5

1、向量

又称矢量，可表示大小、方向等，……

2、向量加法

向量加法原理：eg.向量v3 = 向量v1 + 向量v2，

eg.在houdini中添加add节点(添加一个点)、PointWrangle节点，连接并写入以下代码：

vector v1 = set(1.0, 0.5, 0);
vector v2 = set(0.0, 1, 0.5);

v@v1 = v1;  //已设置标记为黄色
v@v2 = v2;  //已设置标记为青色

vector v3 = v1 + v2;    

v@v3 = v3;  //已设置标记为红色

属性标记方法及结果为： 

3、向量减法 

向量减法原理：eg.向量v3 = 向量v1 - 向量v2，

4、练习1——向量与移动

eg.可以利用小球Sphere(polygon)、PointWrangle节点，用以下向量加法代码观察小球的变化：

vector v1 = chv('tranalate');

v@v1 = v1;

vector pos = @P;

pos += v@v1;
@P = pos;

eg.可以利用小球Sphere(polygon)、PointWrangle节点，用以下向量减法代码观察小球的变化：

vector v1 = rand(@P);
vector v2 = set(0.5, 0.5, 0.5);

v@v1 = v1;
v@v2 = v2;

vector v3 = v1 - v2;

v@v3 = v3;

@P += v@v3;

5、练习2——连接俩向量

eg.假设空间中有两个点A、B，(A—>B的向量距离为)V=B-A，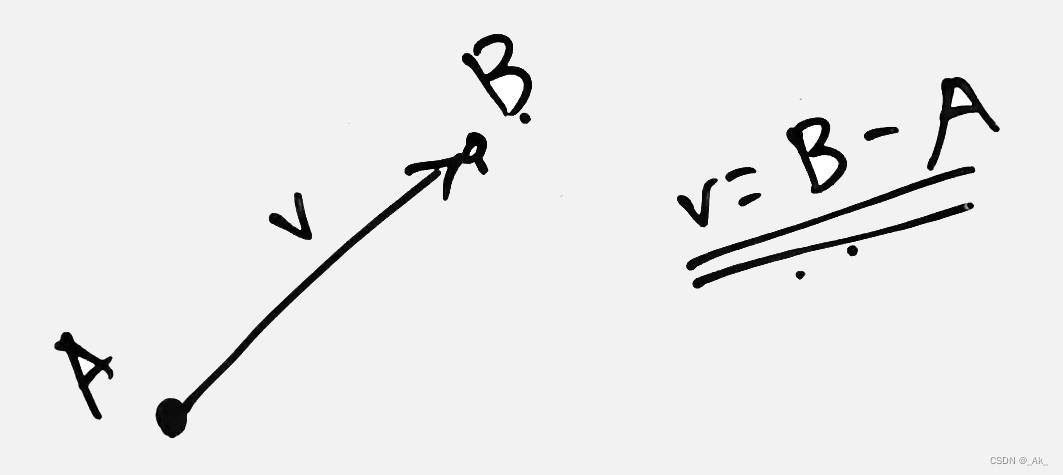

再假设添加一个坐标原点，如下图：

结果似乎与前面所说的【3、Vector Subtraction向量减法 】相违背，其实这两种结果是相同的，因为向量仅显示方向和大小，而没有真正显示它从哪里开始，坐标原点也是一个假设点，也可以假设A为坐标原点。

eg.添加PointWrangle节点、Add1节点(添加一个点A)(随便移动下，连接第1个输入点)、Add2节点(添加一个点B)(随便移动下，连接第2个输入点)：

vector npos = point(1, 'P', 0);    //获取B点坐标

vector dir = npos - @P;    //A——>B的向量(方向、大小)等于B-A

v@v1 = dir;

 结果为：

对两点连成线，操作为：添加一个PointWrangle节点写入以下代码：

vector newpos = @P + v@v1;      //B点

int npt = addpoint(0, newpos);  //A点
int line = addprim(0, 'polyline', @ptnum, npt); //连线
//结果：略

6、练习3——螺旋线

创建一个Add节点(添加一个点)，PointWrangle节点写入以下代码：

vector pos = @P;    //获取Add节点的点
int pt = @ptnum;    //获取Add节点的点
    
for(int i=0; i<10; i++){
    vector dir = set(0, 0, chf('width'));   //每次循环递增的距离
    setpointattrib(0, 'v1', pt, dir);
    
    vector newpos = pos + dir;  
    
    pt = addpoint(0, newpos);
    
    pos = newpos;
}

结果为：（黄色为标记线）

 修改代码，使用三角函数及增加循环次数，使线呈螺旋状：

vector pos = @P;    //获取Add节点的点
int pt = @ptnum;    //获取Add节点的点
    
for(int i=0; i<100; i++){
    float ang = chf('ang') * $PI * i;       //递增角度
    vector dir = set(cos(ang), chf('height'), sin(ang) );   //下一个点
    setpointattrib(0, 'v1', pt, dir);
    
    vector newpos = pos + dir;  
    
    pt = addpoint(0, newpos);
    
    pos = newpos;
}    //结果为一条螺旋线

7、向量与浮点运算

与一般加减乘除相同，下图为向量与浮点float的加法：

减乘除法类似，不再赘述。

8、练习4——向量与缩放

使用小球中心点位置进行缩放。

eg.按下图创建节点并写入代码(add节点随便移动下位置)：

float scale = chf('scale');

@P *= scale;

滑动scale值，结果为：小球仍以世界原点(0,0,0)的中心点进行缩放，

解决办法：①先把小球移动到世界原点(0,0,0)，②进行缩放，③再移动回去。
代码修改为：

float scale = chf('scale');     //缩放系数
vector cen = point(1, 'P', 0);  //Add节点的点位置，即小球的中心点位置（也可以理解为小球的位置，因为已使用copytopoints节点)

@P -= cen;      //小球(中心点)移动到原点

@P *= scale;    //小球缩放

@P += cen;      //小球又移回去

节点按以下截图相连：
结果：小球按自己的中心点进行缩放。

9、向量大小和归一化

归一化函数 normalize() ,，向量仅被视为方向，大小为1。
eg.创建一个Add节点(添加一个点)、一个PointWrangle节点写入以下代码：

vector v1 = set(3.0, 0, 0);

v@v1 = v1;                //黄色
v@v2 = normalize(v1);    //青色，归一化，与v1同方向，向量大小始终为1

f@mag1 = length(v@v1);  //表格结果为3.0
f@mag2 = length(v@v2);  //表格结果为1.0

结果为：归一化后，v2（青色）与v1（黄色）同方向，向量大小为1，表格结果略，

10、练习5——小球缩放

eg.创建一个小球Sphere节点、一个PointWrangle节点写入以下代码：

float rnd = rand(@P);   //随机0~1

vector v1 = @P * rnd;   //

if(chi('use_normalize') == 1){    //设置一个开关按钮：是否把v进行归一化
    v1 = normalize(v1);
}

@P += v1 * chf('mult');     //小球放大

结果：勾选开关按钮，小球均匀随机放大；否则小球每个点随机放大。感兴趣可以自行尝试，并添加属性、标记等，查看更直观的结果。

【后面的向量点积与叉乘，可以先看这里：点击直达】

11、向量点积

可以理解为一个向量在另一个向量上的投影长度。
两个向量相乘得到一个浮点float值，float值计算如下：

扩展：点积的几何意义，可计算夹角/判断大概朝向
从几何角度看，点积是两个向量的长度与它们夹角余弦cos的积。
所以还可以用公式a·b = |a| x |b| x cos(θ) 计算点积，
a·b>0 方向基本相同，夹角在0°到90°之间
a·b=0 正交，相互垂直
a·b<0 方向基本相反，夹角在90°到180°之间

eg.创建一个Add节点(添加一个点)、一个PointWrangle节点写入以下代码：eg.创建一个Add节点(添加一个点)、一个PointWrangle节点写入以下代码：

vector v1 = set(1.0, 0.0, 0.0);
vector v2 = set(chf('x'), 1.0, 0.0);

v@v1 = v1;
v@v2 = v2;

float val = dot(v2, v1);
f@dot = val;    //@dot值 = chf('x')值

结果：略（感兴趣可以给属性@dot添加标记查看结果）

eg.修改上面的代码，给v2添加角度通道，查看不同角度点积值的变化：

float ang = chf('ang') *$PI * 2.0;

vector v1 = set(1.0, 0.0, 0.0);
vector v2 = set(cos(ang), sin(ang), 0.0);

v@v1 = v1;
v@v2 = v2;

float val = dot(v2, v1);
f@dot = val;    //@dot值-1~1,夹角在到0到90°之间为正数，90°为0，夹角在90°到180°之间为负数

结果：略（感兴趣可以给属性@dot添加标记查看结果）

12、练习6——最近点

eg.创建一个Add节点(添加一个点随便移动下)、Sphere节点(半径1、polygon)和法线Normal节点(Points)、PointWrangle节点(Add连第一个输入点、Normal连第二个输入点)，写入以下代码：

int npt = nearpoint(1, @P);         //小球与Add的点 最近的点
vector npos = point(1, 'P', npt);   //最近点的位置
vector nnorm = point(1, 'N', npt);  //最近点的法线方向

vector dir = npos - @P;     //Add的点到最近点
v@v1 = dir;
v@v2 = nnorm;               //Add的点到最近点法线方向

点在小球内时，两线方向接近但并不完全相同，结果为：

点在小球外时，结果为：

继续操作，计算这两个向量之间的点积，用点积值判断点是否在小球内：
继续添加代码：

float val = dot(dir, nnorm);    //计算点积值
//f@dot = val;

if(val > 0){   
    v@Cd = set(1, 0, 0);    //点设置为红色
}else{        
    v@Cd = set(0, 0, 1);   //点设置为蓝色
}

结果： 点积值>0，则点在小球内；点积值<0，则点在小球外。感兴趣的可以把点替换成其他对象，及标记点积值属性，观察其在小球内外的颜色变化

13、向量叉乘

叉乘又叫向量积，可以理解为计算某一个面的法向量。常用于定向、旋转、旋转轴等。
两个向量叉乘(a x b)得到一个向量，该向量垂直于a、b，也可以叫这个向量为a、b平面的法线向量。如果以向量a、b构成一个平面四边形，那a、b的叉乘的模长【 |a||b|sin(θ) 】等于这个平行四边形的面积。

扩展：叉乘计算公式——>点击直达连接

eg.创建一个Add节点(添加一个点)、一个PointWrangle节点写入以下代码:

float ang = chf('ang') * $PI * 2;

vector v1 = set(1.0, 0.0, 0.0);
vector v2 = set(0.0, cos(ang), sin(ang));

v@v1 = v1;    //黄色
v@v2 = v2;    //青色

vector val = cross(v@v1, v@v2);
v@v3 = val;    //红色

结果为：滑动改变角度猴子，v3始终垂直于v1、v2(组成的平面)，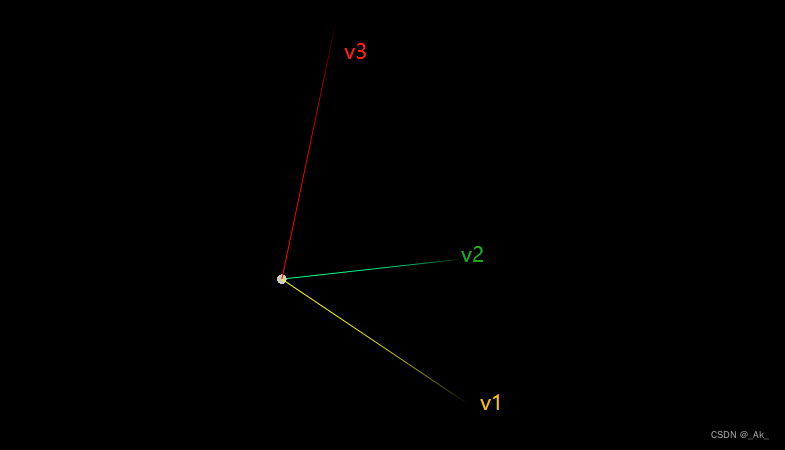

14、练习7——定向

Houdini默认的Up属性：是控制物体y轴方向，也就是局部坐标的向上的方向，一般是(0, 1, 0)，点击查看官方文档介绍。

eg.下面利用Up属性来进行定向(控制总朝向)：
①创建一个Sphere节点(半径1、polygon)和法线Normal节点(Points)、PointWrangle节点，写入以下代码：

vector v1 = set(0.0, 1.0, 0.0);     //设置朝向，可以是任何向量
vector v2 = @N;                     //小球的点法线
    
v@v1 = v1;    //黄色
v@v2 = v2;    //青色

vector crossv = cross(v1, v2);      //叉乘值，法线与自定义向量的垂直向量
v@v3 = crossv;  //红色

结果为：

②继续添加代码：

if(chi('use_cross') ==1){       //自定义开关按钮
    v@up = crossv;
    //整段代码也可以直接用：setpointattrib(0, 'up', @ptnum, set(0, 1, 0));
    //也能达到相同的效果
    //可以理解为up属性的原理
}

 ③添加box节点(polygon)、copytopoints节点(box连第一个输入点，PointWrangle连第二个输入点)

切换开关按钮，自定义朝向前后的结果为：由此可知，Up属性来进行定向(控制总朝向)，