我们这章要设计计算机中的控制器D(z),D(z)是Z域中的表达,是输出信号的Z变换与输入信号Z变换的比值,这个比值等式映射到时域中就是
,这就是我们要找的时域中的控制算法。
计算机控制系统典型图:
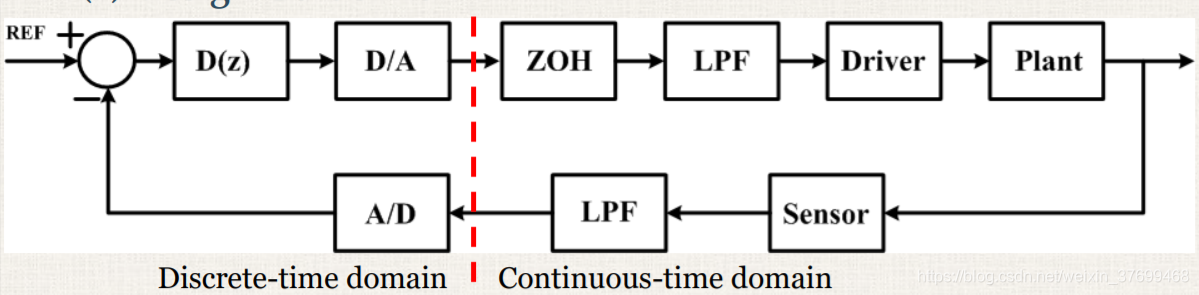
我们假设:A/D D/A转换器的精度足够高,采样没有延迟,上述框图可以简化为下面框图:
。。。略过一些前面的东西,不太明白,过段时间再来补充
模拟控制器的离散化方法
下面我们均认为模拟控制器已经被设计出来了,表示为G(s)。
1、直接Z变换方法或者叫做Impulse Invariance(脉冲响应不变法)
我们可以直接对模拟控制器G(s)进行Z变换得到G(z)。
有人问了,什么尼玛叫做对G(s)进行Z变化,难道Z变换不是针对离散信号的嘛?至少我们信号课上没讲过。。。
请看下图:
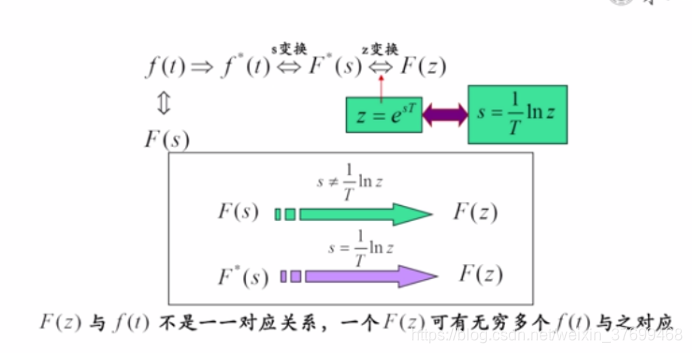
对G(s)进行Z变换的“物理意义”就是:G(s)有一个一一对应的时域信号g(t),时域信号采样得到g*(t),然后对这个离散信号进行Z变换得到G(z)。具体Z变换请看我的另一篇博文《计算机控制系统中的Z变换》。
那么为什么又叫做,impulse invariance法呢?先来看看impulse invariance法的定义:
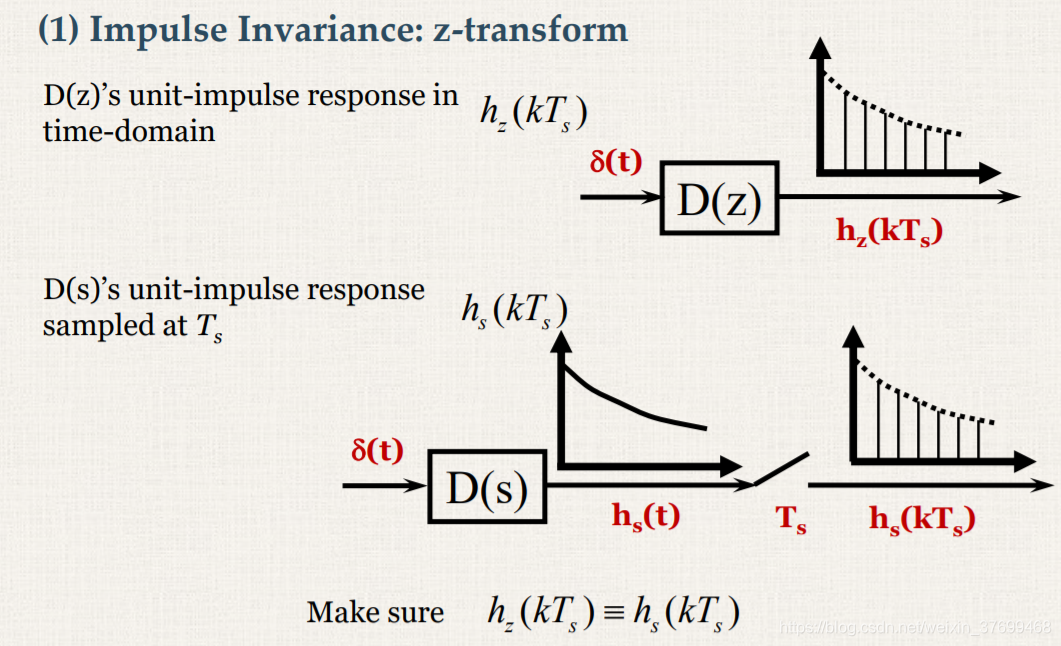
我们对G(s)输入一个脉冲信号,输出是hs(t),hs(t)是什么,就是g(t),即G(s)的拉普拉斯反变换;我们对G(z)也输入一个脉冲信号,得到输出hz(t),我们希望hs(t)采样之后时刻与hz(t)相等,那这样的G(z)是什么呢?那就是:
这里求得的G(z)也就是脉冲响应传递函数(impulse transfer function)。
性质:
①若D(s)稳定,那么D(z)稳定;(原因是:这直接是Z变换)
②频率周期性混叠
(解决频率混叠办法:
 )
)
③ 原因是G(z)不能直接用
替换G(s)得到
④只对可以滤掉高频信号或者本身是低频信号的的系统试用
考试例题:


2、step invariance(阶跃响应不变法)
上一种方法是同时输入脉冲响应,结果相同。这种方法是同时输入阶跃响应,我们要求输出的结果(采样处)相同,如下图:
推导如下:
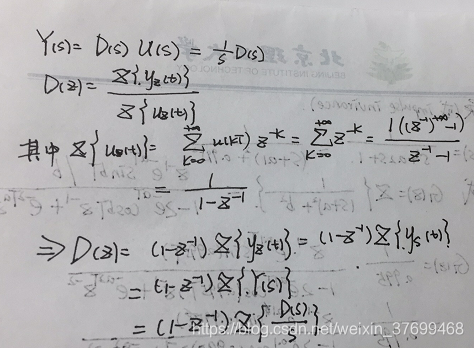
故变换公式为:
说明:相当于D(s)串联一个ZOH然后直接进行Z变换,符合解决方法1种频率混叠的解决方案1,故频率混叠可以被有效减少。
性质:
①D(s)是稳定的,那么D(z)稳定
② 原因是:
不能直接由
得到
③it is applicable for the system which has rich high-frequency information
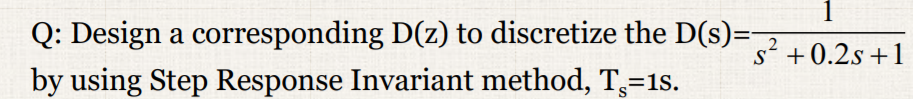


总结有用的z变换公式:
3、差分变换法
设想模拟控制器为一个积分器,于是有,在离散控制器种,用
来表示微分du(t),e(t)dt即这一瞬间的面积可以用两种方法代替,e(kT)T或者e((k-1)T)T,分别对应后向差分和前向差分,即
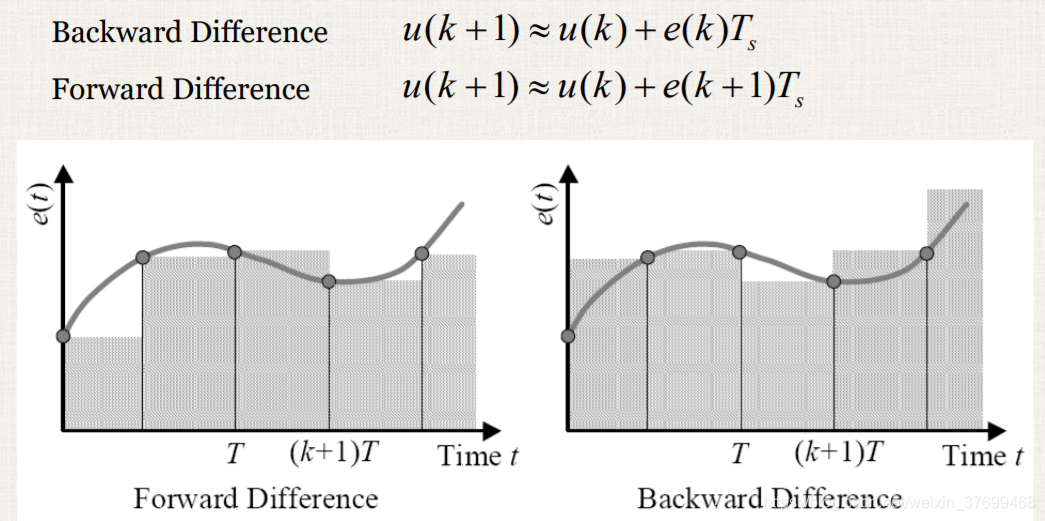
后向差分(backward)
前向差分(forward)
这个对应关系式是直接可以替换的,即用相应的式子替换掉G(s)中的s,即可得到G(z)!
1>前向差分:
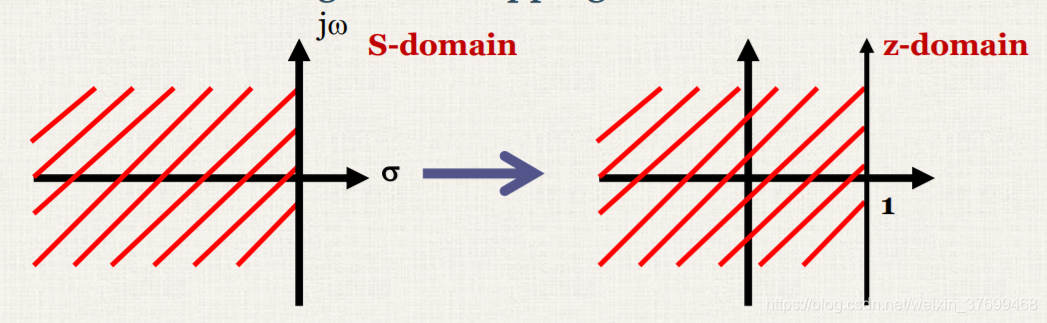

(4)没有频率重叠,但有频率失真!
stability is the foundation of everything, not stable, not useful!基本不用前向差分!!!
2>后向差分
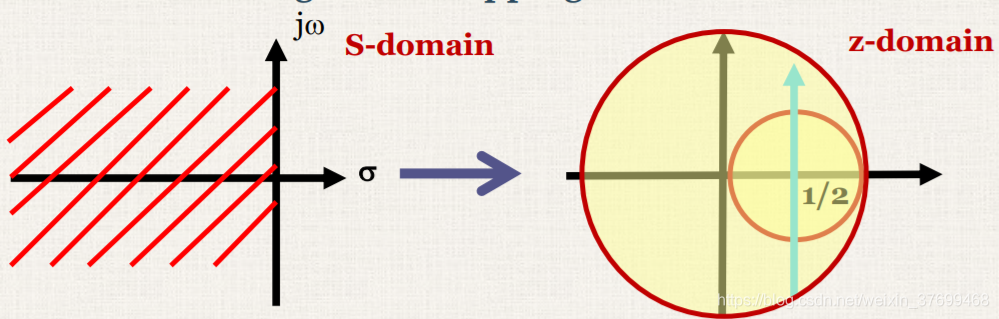

(4)没有频率重叠,变换式一一对应;但是失真严重
考试例题:由于直接代换,相对于前两道题,比较直接

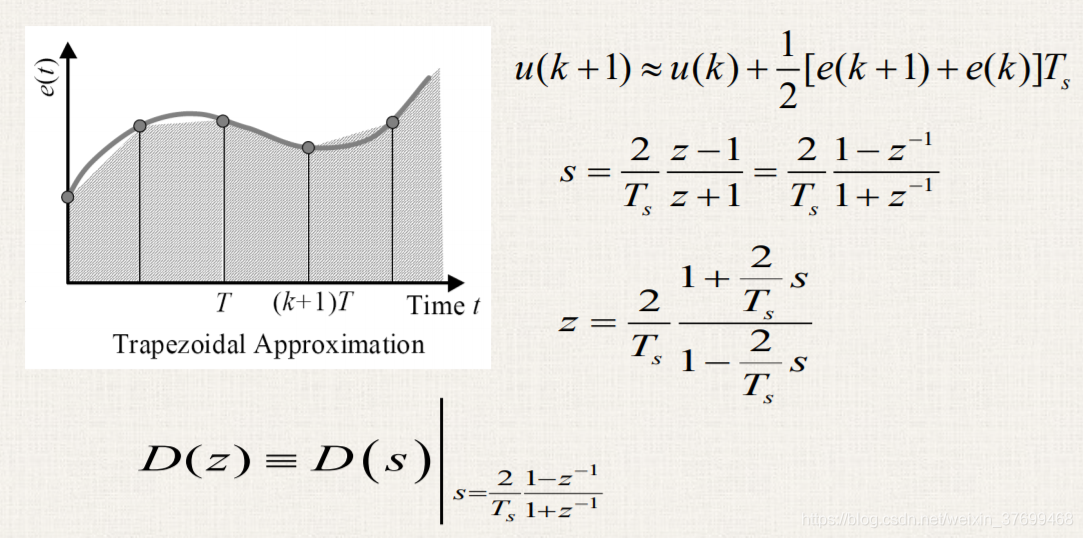
4、双线性变换Tustin
差分法是用矩形面积代替积分面积,双线性是用梯形面积代替积分面积。





 本文深入探讨了将连续时间控制器转换为离散时间控制器的多种方法,包括直接Z变换法(脉冲响应不变法)、阶跃响应不变法、差分变换法及双线性变换法。每种方法的特点、适用条件及可能的问题都被详细解析。
本文深入探讨了将连续时间控制器转换为离散时间控制器的多种方法,包括直接Z变换法(脉冲响应不变法)、阶跃响应不变法、差分变换法及双线性变换法。每种方法的特点、适用条件及可能的问题都被详细解析。
















 1055
1055

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








